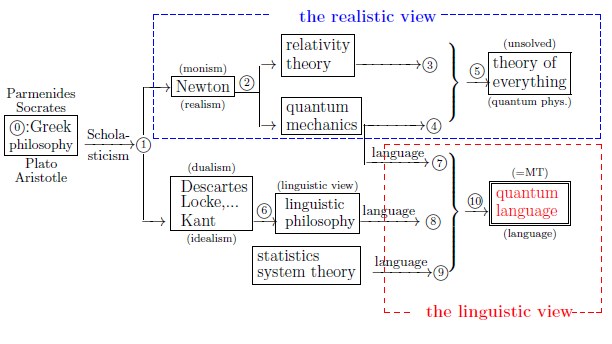
Quantum language is classified by four parts ($(A_1)$, $(A_2)$, $(B_1)$,$(B_2)$) as follows.
$$
\underset{(=\mbox{quantum language})}{\mbox{
measurement theory}}
\left\{\begin{array}{ll}
\underset{\mbox{(A)}}{
\mbox{pure type}}
\left\{\begin{array}{ll}
\!\!
(A_1):\mbox{classical system}
:
\mbox{ Fisher statistics}
\\
\!\!
(A_2):\mbox{ quantum system}
:
\mbox{
usual quantum mechanics
}
\\
\end{array}\right.
\\
\\
\underset{\mbox{(B)}}
{\mbox{mixed type}}
\left\{\begin{array}{ll}
\!\!
(B_1):\mbox{ classical system}
:
\text{including Bayesian statistics, Kalman filter}\\
\!\!
(B_2):\mbox{ quantum system}
:
\mbox{quantum decoherence
}
\\
\end{array}\right.
\end{array}\right.
$$
In this note,
Quantum language (A) has the following stucture: \begin{align} & \underset{\mbox{ (=quantum language)}}{\fbox{pure measurement theory (A)}} := \underbrace{ \underset{\mbox{ ($\S$2.7)}}{ \overset{ [\mbox{ (pure) Axiom 1}] }{\fbox{pure measurement}} } + \underset{\mbox{ ($\S$10.3)}}{ \overset{ [{\mbox{ Axiom 2}}] }{\fbox{Causality}} } }_{\mbox{ a kind of incantation (a priori judgment)}} + \underbrace{ \underset{\mbox{ ($\S$3.1) }} { \overset{ {}}{\fbox{Linguistic interpretation}} } }_{\mbox{ the manual on how to use spells}} \tag{1.2} \end{align}
Since quantum language is a language and not physics, the above axioms (i..e., Axioms1 and 2) are not laws (in phyisics ) but kinds of incantations. That is,
Thus, quantum language says:
Here,
 Axiom 1 (measurement) pure type
( This will be understood in $\S$2.7)
Axiom 1 (measurement) pure type
( This will be understood in $\S$2.7)
With any system $S$, a basic structure $[ {\mathcal A} \subseteq \overline{\mathcal A}]_{B(H)}$ can be associated in which measurement theory of that system can be formulated. In $[ {\mathcal A} \subseteq \overline{\mathcal A}]_{B(H)}$, consider a $W^*$-measurement ${\mathsf M}_{\overline{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F{}), S_{[{}\rho] } \big)$ $\Big($ or, $C^*$-measurement ${\mathsf M}_{{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F{}), S_{[{}\rho] } \big)$ $\Big)$. Then, the probability that a measured value $x$ $( \in X )$ obtained by the $W^*$-measurement ${\mathsf M}_{\overline{\mathcal A}} \bigl({\mathsf O} , S_{[{}\rho{}] } \bigl)$ $\Big($ or, $C^*$-measurement ${\mathsf M}_{{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F{}), S_{[{}\rho] } \big)$ $\Big)$ belongs to $ \Xi $ $(\in {\cal F}{})$ is given by \begin{align} \rho( F(\Xi)) (\equiv {}_{{{\mathcal A}^*}}(\rho, F(\Xi) )_{\overline{\mathcal A}} ) \tag{1.3} \end{align}
 Axiom 2 (causality)
(This will be understood in $\S$10.3)
Axiom 2 (causality)
(This will be understood in $\S$10.3)
Let $T$ be a tree (i.e., semi-ordered tree structure). For each $t (\in T)$, a basic structure $[{\mathcal A}_t \subseteq \overline{\mathcal A}_t]_{ B(H_t)}$ is associated. Then, the causal chain is represented by a $W^*$- sequential causal operator $ \{ \Phi_{t_1,t_2}{}: $ ${\overline{\mathcal A}_{t_2}} \to {\overline{\mathcal A}_{t_1}} \}_{(t_1,t_2) \in T^2_{\leqq}}$ $\Big($ or, $C^*$- sequential causal operator $ \{ \Phi_{t_1,t_2}{}: $ ${{\mathcal A}_{t_2}} \to {{\mathcal A}_{t_1}} \}_{(t_1,t_2) \in T^2_{\leqq}}$ $\Big)$
If it's learned by rote, repeat it many times. That is,
This is everything of quantum language. However, if the readers would like to make progress quantum language early, the manual on how to use Aioms 1 and 2 is convenient. Thus, I consider that
| $\fbox{Note 1.3}$ | If metaphysics did something wrong in
the history of science, it is because metaphysics attempted to answer following questions seriously in ordinary language:
Although this question $(\sharp_1)$ looks attractive, however, it is not productive. What is important is So we replace the ($\sharp_1$) by the following ($\sharp_2$):
The problem ($\sharp_1$) will now be solved in the sense of ($\sharp_2$). 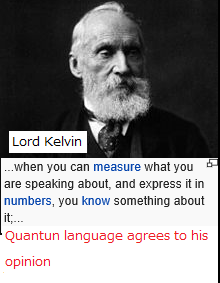
|
| $\fbox{Note 1.4}$ | Metaphysics is an academic discipline concerning the propositions in which empirical validation is impossible. Lord Kelvin(1824--1907), who is famous as the absolute temperature $K$, said that
See the following ref.
|