Let us explain the
moment method,
which as well as Fisher's maximum likelihood method are frequently used.
Consider the measurement ${\mathsf M}_{\cal A} \bigl({\mathsf O} \equiv (X,{\mathcal F}, F) ,$ $ S_{[\rho] } \bigl)$, and its parallel measurement $\otimes_{k=1}^n {\mathsf M}_{\cal A} \bigl({\mathsf O} $ $\equiv (X,{\mathcal F}, F) ,$ $ S_{[\rho] } \bigl)$ (= ${\mathsf M}_{\otimes {\cal A}} \big( \bigotimes_{k=1}^n {\mathsf O} := ( X^n,{\mathcal F}^n, \bigotimes_{k=1}^n F ) , S_{ [{}\otimes_{k=1}^n \rho{}]}{}\big)$. Assume that the measured value $(x_1,$ $ x_2 ,$ $...$, $ x_n ) (\in X^n)$ is obtained by the parallel measurement. Assume that $n$ is sufficiently large. By the law of large numbers (Theorem 4.5), we can assure that
$(A):$ in order to infer the unknown state $\rho (\in {\frak S}^p({\mathcal A}^*))$, it suffices to solve the equation (5.18)

| $(B_1):$ | Solve the following equation: \begin{align} \| \nu_n(\cdot ) - \rho(F(\cdot ))\|_{{\mathcal M}(X)} = \min \{ \| \nu_n(\cdot ) - \rho_1(F(\cdot ))\|_{{\mathcal M}(X)} \;| \; \rho_1 (\in {\frak S}^p({\mathcal A}^*)) \} \tag{5.19} \end{align} |
| $(B_2):$ | For some $f_1, f_2, \cdots , f_n$ $\in C(X)$ $(= \mbox{the set of all continuous functions on $X$} )$, it suffices to find $ \rho (\in {\frak S}^p({\mathcal A}^*)) $ such that $\Delta (\rho)=\min_{\rho_1 (\in {\frak S}^p({\mathcal A}^*))} \Delta(\rho_1)$, where \begin{align} \Delta (\rho)= & \sum_{k=1}^n \Big| \int_X f_k(\xi) \nu_n (d \xi ) - \int_X f_k(\xi) \rho( F(d \xi )) \Big| \\ = & \sum_{k=1}^n \Big| \frac{f_k({x_1})+f_k({x_2})+ \cdots + f_k({x_n})}{n} - \int_X f_k(\xi) \rho( F(d \xi )) \Big| \end{align} |
| $(B_3):$ | In the cases of the classical measurement ${\mathsf M}_{L^\infty (\Omega)} \bigl({\mathsf O} \equiv (X,{\mathcal F}, F) ,$ $ S_{[\rho] } \bigl)$ (putting $\rho=\delta_{\omega}$), it suffices to solve \begin{align} 0= \sum_{k=1}^n \Big| \frac{f_k({x_1})+f_k({x_2})+ \cdots + f_k({x_n})}{n} - \int_X f_k(\xi) [F(d \xi )](\omega) \Big| \tag{5.20} \end{align} or, it suffices to solve \begin{align} \left\{\begin{array}{ll} \frac{f_1({x_1})+f_1({x_2})+ \cdots + f_1({x_n})}{n} - \int_X f_1(\xi) [F(d \xi )](\omega)=0 \\ \\ \frac{f_2({x_1})+f_2({x_2})+ \cdots + f_2({x_n})}{n} - \int_X f_2(\xi) [F(d \xi )](\omega)=0 \\ \qquad \dots \dots \\ \qquad \dots \dots \\ \frac{f_m({x_1})+f_m({x_2})+ \cdots + f_m({x_n})}{n} - \int_X f_m(\xi) [F(d \xi )](\omega)=0 \end{array}\right. \end{align} |
| $(B_4)$: | Particularly, in the case that $X=\{\xi_1, \xi_2, \cdots , \xi_m \}$ is finite, define $f_1, f_2, \cdots , f_m$ $\in C(X)$ by \begin{align} f_k(\xi) = \chi_{{}_{\{\xi_k \}}}(\xi)=\left\{\begin{array}{ll} 1 \quad & (\xi= \xi_k) \\ 0 & ( \xi \not=\xi_k ) \end{array}\right. \end{align} and, it suffices to find the $\rho (= \delta_\omega )$ such that \begin{align} & \sum_{k=1}^n \Big| \frac{ \chi_{{}_{\{\xi_k \}}}({x_1})+ \chi_{{}_{\{\xi_k \}}}({x_2})+ \cdots +\chi_{{}_{\{\xi_k \}}} ({x_n})}{n} - \int_X \chi_{{}_{\{\xi_k \}}}( \xi) \rho( F(d \xi )) \Big| \\ = & \sum_{k=1}^n \Big| \frac{\sharp[\{x_m \;:\; \xi_k=x_m \}]}{n} - [F( \{ \xi_k\} ](\omega ) ) \Big|=0 \end{align} |
| $(C_1):$ | It is desirable that $n$ is sufficiently large, but the moment method may be valid even when $n=1$. |
| $(C_2)$: | The choice of $f_k$ is artificial ( on the other hand, Fisher' maximum likelihood method is natural). |
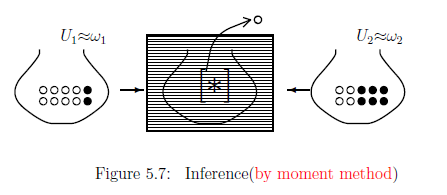
Consider the measurement ${\mathsf M}_{{L^\infty (\Omega) }} ({\mathsf O} {{=}}$ $ ( \{ w,$ $ b \},$ $ 2^{\{ w, b \} } ,$ $ F) , S_{ [{}{\ast}]})$. Here, recall that the observable ${\mathsf O}_{wb} = ( \{ w, b \}, 2^{\{ w, b \} } , F_{wb})$ in $L^\infty(\Omega)$ is defined by
\begin{align} & [F_{wb}(\{ w \})](\omega_1)= 0.8, & \quad & [ F_{wb}(\{ b \})](\omega_1)= 0.2 \nonumber \\ & [F_{wb}(\{ w \})](\omega_2)= 0.4, & \quad & [F_{wb}(\{ b \})] (\omega_2)= 0.6 \nonumber \end{align}Since a measured value "w" is obtained, the approximate sample space $( \{ w, b \}, 2^{\{ w, b \} } , \nu_1)$ is obtained as
\begin{align} \nu_1(\{ w \})=1, \quad \nu_1(\{b \})=0 \end{align}[(i): when the unknown state $[\ast]$ is $\omega_1$]
\begin{align} (5.19)=|1-0.8|+|0-0.2| \end{align}[(ii):when the unknown state $[\ast]$ is $\omega_2$]
\begin{align} (5.19)=|1-0.4|+|0-0.6| \end{align}Thus, by the moment method, we can infer that $[\ast]=\omega_1$, that is, the urn behind the curtain is $U_1$.
The above may be too easy. Thus, we add the following problem.
| $(a):$ | Which the urn behind the curtain is $U_1$ or $U_2$? |
Consider the simultaneous measurement ${\mathsf M}_{{L^\infty (\Omega) }} (\times_{k=1}^{7}{\mathsf O} {{=}}$ $ ( \{ w, b \}^7,$ $ 2^{{\{ w, b \} }^7} ,$ $\times_{k=1}^{7} F) ,$ $ S_{ [{}{\ast}]})$. And assume that the measured value is $(w, b, b, w, b, w, b)$. Then, [(i): when $[\ast]$ is $\omega_1$]
\begin{align} (5.19) =|3/7-0.8|+|4/7-0.2|=52/70 \end{align}[(ii):when $[\ast]$ is $\omega_2$]
\begin{align} (5.19) =|3/7-0.4|+|4/7-0.6|=10/70 \end{align}Thus, by the moment method, we can infer that $[\ast]=\omega_2$, that is, the urn behind the curtain is $U_2$.
Example 5.13 [The most important example of moment method]
Putting $\Omega={\mathbb R} \times {\mathbb R}_+$ $=\{ \omega =(\mu , \sigma ) \; |\; \mu \in {\mathbb R}, \sigma >0 \}$ with Lebesgue measure $\nu$, Consider the classical basic structure
\begin{align} [ C_0(\Omega ) \subseteq L^\infty(\Omega,\nu) \subseteq B(L^2(\Omega,\nu))] \end{align}Assume that the observable ${\mathsf O}_{G} $ ${{=}}$ $(X(={}{\mathbb R}) , {\cal B}_{{\mathbb R}}^{} , G)$ in $L^\infty ({\Omega}{}, \nu)$ satisfies that
\begin{align} & \int_{\mathbb R} \xi [G( d \xi )](\mu, \sigma )=\mu, \quad \int_{\mathbb R} (\xi -\mu)^2 [G( d \xi )](\mu, \sigma )=\sigma^2 \\ & \quad \qquad ( \forall {\omega}=(\mu, \sigma) \in \Omega (={\mathbb R} \times {\mathbb R}_+ )) \end{align}Here, assume that a measured value $(x_1, x_2, x_3 ) (\in {\mathbb R}^3)$ is obtained by the simultaneous measurement $\times_{k=1}^3{\mathsf M}_{L^\infty(\Omega )} ({\mathsf O}_{G}, S_{[{}\ast{}] })$. That is, we have the $3$-sample distribution $\nu_3$ such that
\begin{align} \nu_3 = \frac{ \delta_{x_1}+\delta_{x_2}+\delta_{x_3}}{3} \in {\mathcal M}_{+1}({\mathbb R}) \end{align} Put $f_1(\xi)=\xi, f_2(\xi)=\xi^2$. Then, by the moment method (5.20), we see: \begin{align} 0=& \sum_{k=1}^2 \Big| \int_{\mathbb R} \xi^k \nu_3 (d \xi ) - \int_{\mathbb R} \xi^k [G(d \xi )](\omega) \Big| \\ = & \sum_{k=1}^2 \Big| \frac{({x_1})^k+({x_2})^k+ ({x_n})^k}{3} - \int_{\mathbb R} \xi^k [G(d \xi )](\mu, \sigma) \Big| \\ = & \Big| \frac{{x_1}+{x_2}+ {x_3}}{3} - \mu \Big| + \Big| \frac{({x_1})^2+({x_2})^2+ ({x_3})^2}{3} - (\sigma^2 + \mu^2 ) \Big| \end{align} Thus, we get: \begin{align} \mu &=\frac{{x_1}+{x_2}+ {x_n}}{3} \\ \sigma^2 & = \frac{({x_1})^2+({x_2})^2+ ({x_3})^2}{3} -\mu^2 \\ & = \frac{({x_1}- \frac{{x_1}+{x_2}+ {x_n}}{3} )^2+({x_2}- \frac{{x_1}+{x_2}+ {x_n}}{3} )^2+ ({x_3} - \frac{{x_1}+{x_2}+ {x_n}}{3} )^2}{3} \end{align} which is the same as the (5.13) concerning the normal measurement.| $\fbox{Note 5.3}$ | Consider the measurement ${\mathsf M}_{L^\infty(\Omega)}({\mathsf O} {{=}} (X,2^X,$ $ F),$ $ S_{[\ast]} )$, where $X= \{x_1,x_2,...,x_n\}$ is finite. Then, we see that
\begin{align}
\mbox{"Fisher's maximum likelihood method"="moment method"}
\end{align}
[Answer] Assume that a measured value$x_m (\in X)$ is obtained by the measurement ${\mathsf M}_{\overline{\mathcal A}}({\mathsf O} {{=}} (X,2^X,$ $ F),$ $ S_{[\ast]} )$
[Fisher's maximum likelihood method]:
|
