5.6: The two envelope problem; non-baysian approach

| $(a):$ | $\qquad \frac{V_1}{V_2}=1/2$ or, $\frac{V_1}{V_2}=2$ |

5.6.2 Answer: the two envelope problem
Consider the classical basic structure \begin{align} { [ C_0(\Omega ) \subseteq L^\infty ( \Omega , \nu ) \subseteq B(L^2 ( \Omega , \nu ) ) ] } \end{align}where the locally compact space $\Omega$ is arbitrary, that is, it may be $\overline{\mathbb R}_+ =\{ \omega \;|\;\mbox{$\omega \ge 0$} \}$ or the one point set $\{ \omega_0 \}$ or $\Omega =\{ 2^n \;|\; n=0, \pm 1, \pm 2, \ldots \}$. Put $X=\overline{\mathbb R}_+ =\{ x \;|\;\mbox{$x \ge 0$} \}$. Consider two continuous (or generally, measurable ) functions $V_1: \Omega \to \overline{\mathbb R}_+$ and $V_2: \Omega \to \overline{\mathbb R}_+$. such that
\begin{align} V_2(\omega)=2V_1(\omega) \mbox{ or,}\;\; 2V_2(\omega)=V_1(\omega) \quad (\forall \omega \in \Omega ) \end{align}For each $k=1,2$, define the observable ${\mathsf O}_k=(X(=\overline{\mathbb R}_+), {\mathcal F}(={\mathcal B}_{\overline{\mathbb R}_+}:\mbox{the Borel field}), F_k )$ in $L^\infty (\Omega, \nu )$ such that
\begin{align} & \qquad [F_k(\Xi )](\omega )= \left\{\begin{array}{ll} 1 \qquad & (\mbox{ if } V_k(\omega) \in \Xi) \\ 0 \qquad & (\mbox{ if } V_k(\omega) \notin \Xi) \end{array}\right. \\ & (\forall \omega \in \Omega, \forall \Xi \in {\mathcal F} ={\mathcal B}_{\overline{\mathbb R}_+} \mbox{ i.e., the Bore field in $X(=\overline{\mathbb R}_+)$ } ) \end{align}Furthermore, define the observable ${\mathsf O}=(X, {\mathcal F}, F )$ in $L^\infty (\Omega ,\nu)$ such that
\begin{align} F(\Xi)=\frac{1}{2} \Big( F_1(\Xi)+F_2(\Xi) \Big) \quad (\forall \Xi \in {\mathcal F}) \tag{5.23} \end{align} That is, \begin{align} & \qquad [F(\Xi )](\omega )= \left\{\begin{array}{ll} 1 \qquad & (\mbox{ if } V_1(\omega) \in \Xi, \;\; V_2(\omega) \in \Xi) \\ 1/2 \qquad & (\mbox{ if } V_1(\omega) \in \Xi, \;\; V_2(\omega) \notin \Xi) \\ 1/2 \qquad & (\mbox{ if } V_1(\omega) \notin \Xi, \;\; V_2(\omega) \in \Xi) \\ 0\qquad & (\mbox{ if } V_1(\omega) \notin \Xi, \;\; V_2 (\omega) \notin \Xi) \end{array}\right. \\ & (\forall \omega \in \Omega, \forall \Xi \in {\mathcal F}={\mathcal B}_X \mbox{ i.e., $\Xi$ is a Borel set in $X(=\overline{\mathbb R}_+)$ } ) \end{align}Fix a state $\omega (\in \Omega )$, which is assumed to be unknown. Consider the measurement ${\mathsf M}_{L^\infty(\Omega, \nu )} ({\mathsf O}=(X, {\mathcal F} , F ), S_{[\omega]})$. Axiom 1 ($\S$2.7) says that
| $(A_1):$ | the probability that a measured value $ \left\{\begin{array}{ll} V_1(\omega) \\ V_2(\omega) \end{array}\right\} $ is obtained by the measurement $ \left.\begin{array}{l} {\mathsf M}_{L^\infty(\Omega, \nu )} ({\mathsf O}=(X, {\mathcal F} , F ), S_{[\omega]}) \\ {} \end{array}\right. $ is given by $ \left\{\begin{array}{ll} 1/2 \\ 1/2 \end{array}\right\} $ |
If you switch to $ \left\{\begin{array}{ll} V_2(\omega) \\ V_1(\omega) \end{array}\right\} $, your gain is $ \left\{\begin{array}{ll} V_2(\omega) - V_1(\omega)= \omega \\ V_1(\omega) - V_2(\omega)=- \omega \end{array}\right\} $. Therefore, the expectation of switching is \begin{align} (V_2(\omega) - V_1(\omega))/2 + ( V_1(\omega) - V_2(\omega))/2 = 0 \end{align}
That is, it is wrong "The Other Person's envelope is Always Greener".
Remark 5.17 The condition (a) in Problem 5.16 is not needed. This condition plays a role to confuse the essence of the problem.
5.6.3 Another answer: the two envelope problem 5.16Problem
For the preparation of the following section ($\S$ 5.6.4), consider the state space $\Omega$ such that
\begin{align} \Omega=\overline{\mathbb R}_+ \end{align} with Lebesgue measure $\nu$. Thus, we start from the classical basic structure \begin{align} [ C_0(\Omega ) \subseteq L^\infty ( \Omega , \nu ) \subseteq B(L^2 ( \Omega , \nu ) ) ] \end{align}Also, putting $\widehat{\Omega}=\{ (\omega, 2 \omega ) \;| \; \omega \in \overline{\mathbb R}_+ \}$, we consider the identification:
\begin{align} \Omega \ni \omega \underset{\mbox{(identification)}}{\longleftrightarrow} (\omega, 2 \omega ) \in \widehat{\Omega} \tag{5.24} \end{align}Furthermore, define $V_1:\Omega (\equiv \overline{\mathbb R}_+) \to X(\equiv \overline{\mathbb R}_+)$ and $V_2:\Omega (\equiv \overline{\mathbb R}_+) \to X(\equiv \overline{\mathbb R}_+)$ such that
\begin{align} V_1(\omega ) =\omega , \quad V_2(\omega ) = 2 \omega \qquad (\forall \omega \in \Omega) \end{align}And define the observable ${\mathsf O}=(X(=\overline{\mathbb R}_+), {\mathcal F}(={\mathcal B}_{\overline{\mathbb R}_+}:\mbox{ the Borel field}), F )$ in $L^\infty (\Omega, \nu )$ such that
\begin{align} & \qquad [F(\Xi )](\omega )= \left\{\begin{array}{ll} 1 \qquad & (\mbox{ if } \omega \in \Xi, \;\; 2 \omega \in \Xi) \\ 1/2 \qquad & (\mbox{ if } \omega \in \Xi, \;\; 2 \omega \notin \Xi) \\ 1/2 \qquad & (\mbox{ if } \omega \notin \Xi, \;\; 2 \omega \in \Xi) \\ 0 \qquad & (\mbox{ if } \omega \notin \Xi, \;\; 2 \omega \notin \Xi) \end{array}\right. \qquad (\forall \omega \in \Omega, \forall \Xi \in {\mathcal F} ) \end{align}Fix a state $\omega (\in \Omega )$, which is assumed to be unknown. Consider the measurement ${\mathsf M}_{L^\infty (\Omega, \nu )} ({\mathsf O}=(X, {\mathcal F}, F ), S_{[\omega]})$. Axiom 1 ( measurement: $\S$2.7) says that
| $(A_2):$ | the probability that a measured value $ \left\{\begin{array}{ll} x=V_1(\omega)=\omega \\ x=V_2(\omega ) =2 \omega \end{array}\right\} $ is obtained by ${\mathsf M}_{L^\infty (\Omega, \nu )} ({\mathsf O}=(X, {\mathcal F}, F ), S_{[\omega]})$ is given by $ \left\{\begin{array}{ll} 1/2 \\ 1/2 \end{array}\right\} $ |
If you switch to $ \left\{\begin{array}{ll} V_2(\omega) \\ V_1(\omega) \end{array}\right\} $, your gain is $ \left\{\begin{array}{ll} V_2(\omega) - V_1(\omega) \\ V_1(\omega) - V_2(\omega) \end{array}\right\} $. Therefore, the expectation of switching is
\begin{align} (V_2(\omega) - V_1(\omega))/2 + ( V_1(\omega) - V_2(\omega))/2 = 0 \end{align}That is, it is wrong "The Other Person's envelope is Always Greener".
Remark 5.18 The readers should note that Fisher's maximum likelihood method is not used in the two answers ( in $\S$5.6.2 and $\S$5.6.3). If we try to apply Fisher's maximum likelihood method to Problem 5.16 ( Two envelope problem), we get into a dead end. This is shown below.
5.6.4 Where do we mistake in (P1) of Problem 5.16?
Now we can answer to the question:
| $(a):$ | a measured value $\alpha$ is obtained by the measurement ${\mathsf M}_{L^\infty(\Omega, \nu )} ({\mathsf O}=(X, {\mathcal F}, F ), S_{[\ast]})$ |
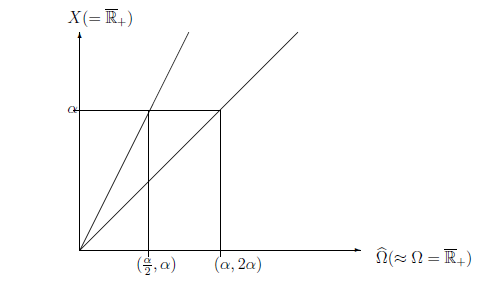
Therefore,Fisher's maximum likelihood method says that
| $(B_1):$ | unknown state $[\ast]$ is equal to $\alpha/2$ or $\alpha$ |
$\Big($ If $[\ast]=\alpha/2$ [resp. $[\ast]=\alpha$ ], then the switching gain is $(\alpha/2-\alpha)$ [resp. $(2\alpha-\alpha)$] $\Big)$. However, Fisher's maximum likelihood method does not say
| $(B_2):$ | $ \left\{\begin{array}{ll} \mbox{"the probability that $[\ast]=\alpha/2$"=1/2 } \\ \mbox{"the probability that $[\ast]=\alpha$"=1/2} \\ \mbox{"the probability that $[\ast]$ is otherwise"=0} \end{array}\right. $ |
Therefore, we can not calculate ( such as (5.22)):
\begin{align} (\alpha/2-\alpha) \times \frac{1}{2} + (2\alpha-\alpha)\times \frac{1}{2} =1.25 \alpha \end{align}| $(C_1):$ | Thus, the sentence "with probability $1/2$" in [(P1):Why is it paradoxical?] is wrong. |
Hence, we can conclude that
| $(C_2):$ | If "state space" is specified, there will be no method of a mistake. |
Remark 5.19 For the Bayesian solution of the two envelope problem 5.16Problem}, see Ch.10.
| $\fbox{Note 5.5}$ | The readers may think that
|
