Given a circle with the radius 1.
Suppose a chord of the circle is chosen { \Large at random}. What is the probability that the chord is shorter than
${\sqrt 3 }$?
Define the rotation map $T_{\mbox{ rot}}^\theta : {\mathbb R}^2 \to {\mathbb R}^2$
$(0\le \theta <2\pi)$
and
the reverse map
$T_{\mbox{ rev}} : {\mathbb R}^2 \to {\mathbb R}^2$
such that
Here, "invariant" means
"invariant concerning the rotation map
$T_{\mbox{ rot}}^\theta$
and reverse map
$T_{\mbox{ rev}}$".
In what follows,
we show that the above invariant measure exists but it is not determined uniquely.
9.12: Bertrand's paradox( "randomness" depends on how you look at)
Theorem9.18 (the principle of equal weight) implies that
However,
this is due to the finiteness of the state space.
In the case of infinite state space,
\begin{align}
\mbox{
"randomness" depends on how you look at
}
\end{align}
This is explained in this section.
$\bullet$
the "randomness" may be related to the invariant probability measure.
9.12.1: Bertrand's paradox("randomness" depends on how you look at)
Here,
let us review the argument about the Bertrand paradox.
Consider the following problem:
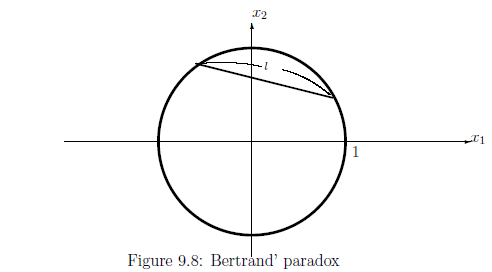
Put $\Omega$
$=\{l \;|\; l \mbox{ is a chord} \}$,
that is,
the set of all chords.
$(A):$
Can we uniquely define an invariant probability measure on $\Omega$?
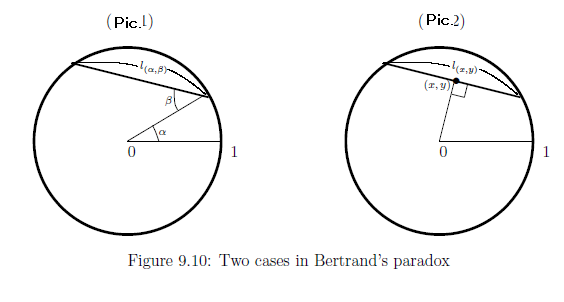
In Fig.$1$, we see that the chord ℓ is represented by a point $(\alpha, \beta) $ in the rectangle $\Omega_1$ $\equiv$ $\{ (\alpha, \beta) \; | \; 0 < \alpha \le 2 \pi, \; 0 < \beta \le \pi/2 \mbox{(radian)}\}$. That is, we have the following identification:
\begin{align} \Omega ( = \mbox{the set of all chords}) \ni \mbox{ℓ}_{(\alpha, \beta)} \underset{\scriptsize{\mbox{identification}}}{\longleftrightarrow} (\alpha , \beta) \in \Omega_1 ( \subset {\mathbb R}^2 ). \end{align}Note that we have the natural probability measure $\nu_1$ on $\Omega_1$ such that $\nu_1 (A) = \frac{ \mbox{Meas}[{}A]}{\mbox{Meas}[{}\Omega_1{}] } = \frac{ \mbox{Meas} [{}A]}{ \pi^2 }$ $(\forall A \in {\cal B}_{\Omega_1})$, where " Meas" = " Lebesgue measure". Transferring the probability measure $\nu_1$ on $\Omega_1$ to $\Omega$, we get $\rho_1$ on $\Omega$. That is,
\begin{align} {\mathcal M}_{+1} (\Omega ) \ni \rho_1 \underset{\scriptsize{\mbox{identification}}}{\longleftrightarrow} \nu_1 \in {\mathcal M}_{+1} (\Omega_1 ) \end{align}| $(\sharp):$ | It is clear that the measure $\rho_1$ is invariant concerning the rotation map $T_{\mbox{ rot}}^\theta$ and reverse map $T_{\mbox{ rev}}$. |
Therefore, we have a natural measurement ${\mathsf M}_{L^\infty ( \Omega, m )}({\mathsf O}_E \equiv (\Omega, {\mathcal B}_{\Omega} , F_E), S_{[\ast]}(\rho_1) )$. Consider the identification:
\begin{align} \Omega \supseteq \Xi_{\sqrt{3}} \underset{\scriptsize{\mbox{identification}}}{\longleftrightarrow} \{ (\alpha , \beta )\in \Omega_1 \;:\; \mbox{"the length of } \mbox{ℓ}_{(\alpha , \beta)}" < {\sqrt 3} \} \subseteq \Omega_1 \end{align}Then, Axiom$^{\mbox{ (m)}}$ 1 ( in $\S$9.1) says that the probability that a measured value belongs to $\Xi_{\sqrt{3}}$ is given by
\begin{align} & \int_{\Omega} [F_E (\Xi_{\sqrt{3}})](\omega) \; \rho_1( d \omega )= \int_{\Xi_{\sqrt{3}}}\;\; 1 \;\; \rho_1( d \omega ) \\ = & m_1 (\{ \mbox{ℓ}_{(\alpha , \beta)} \approx (\alpha, \beta) \in \Omega_1 \; | \; \mbox{ "the length of } \mbox{ℓ}_{(\alpha , \beta)}" \le {\sqrt 3} \}) \\ = & \frac{\mbox{Meas}[{}\{ (\alpha, \beta) \; | \; 0 \le \alpha \le 2 \pi, \;\pi/6 \le \beta \le \pi/2 \}]} {\mbox{Meas}[{}\{ (\alpha, \beta) \; | \; 0 \le \alpha \le 2 \pi, \;0 \le \beta \le \pi/2\}]} \\ = & \frac{2 \pi \times ( \pi/3)} {\pi^2} = \frac{2}{3}. \end{align}
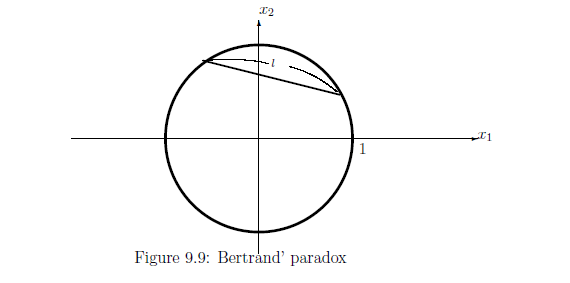
[The second answer (Fig.$2$ (in Figure 9.10))].
In Fig.$2$, we see that the chord ℓ is represented by a point $(x,y) $ in the circle $\Omega_2$ $\equiv$ $\{ (x,y) \; | \; x^2 + y^2 < 1 \}$.
That is, we have the following identification:
\begin{align} \Omega ( = \mbox{the set of all chords}) \ni \mbox{ℓ}_{(x,y)} \underset{\scriptsize{\mbox{identification}}}{\longleftrightarrow} (x,y) \in \Omega_2 ( \subset {\mathbb R}^2 ). \end{align}We have the natural probability measure $\nu_2$ on $\Omega_2$ such that $\nu_2 (A) = \frac{ \mbox{Meas}[{}A]}{\mbox{Meas}[{}\Omega_2{}] } = \frac{ \mbox{Meas} [{}A]}{ \pi }$ $(\forall A \in {\cal B}_{\Omega_2})$. Transferring the probability measure $\nu_2$ on $\Omega_2$ to $\Omega$, we get $\rho_2$ on $\Omega$. That is,
\begin{align} {\mathcal M}_{+1} (\Omega ) \ni \rho_2 \underset{\scriptsize{\mbox{identification}}}{\longleftrightarrow} \nu_2 \in {\mathcal M}_{+1} (\Omega_2 ) \end{align}| $(\sharp):$ | It is clear that the measure $\rho_2$ is invariant concerning the rotation map $T_{\mbox{ rot}}^\theta$ and reverse map $T_{\mbox{ rev}}$.} |
Therefore, we have a natural measurement ${\mathsf M}_{L^\infty ( \Omega, m )}({\mathsf O}_E \equiv (\Omega, {\mathcal B}_{\Omega} , F_E), S_{[\ast]}(\rho_2) )$.
Consider the identification:
\begin{align} \Omega \supseteq \Xi_{\sqrt{3}} \underset{\scriptsize{\mbox{identification}}}{\longleftrightarrow} \{ (x , y )\in \Omega_2 \;:\; \mbox{"the length of } \mbox{ℓ}_{(\alpha , \beta)}" < {\sqrt 3} \} \subseteq \Omega_1 \end{align}Then, Axiom$^{\mbox{ (m)}}$ 1 ( in $\S$9.1) says that the probability that a measured value belongs to $\Xi_{\sqrt{3}}$ is given by
\begin{align} & \int_{\Omega} [F_E (\Xi_{\sqrt{3}})](\omega) \; \rho_2( d \omega )= \int_{\Xi_{\sqrt{3}}}\;\; 1 \;\; \rho_2( d \omega ) \\ = & \nu_2 (\{ \mbox{ℓ}_{(x,y)} \approx (x,y) \in \Omega_2 \; | \; \mbox{ "the length of } \mbox{ℓ}_{(x,y)}" \le {\sqrt 3} \}) \\ = & \frac{\mbox{Meas} [{} \{ (x,y) \; | \; 1/4 \le x^2+y^2 \le 1 \} ]} {\pi} = \frac{3}{4}. \end{align}
Thus, even if there is a custom to regard a natural probability measure (i.e., an invariant measure concerning natural maps) as "random", the first answer and the second answer say that
| $(\sharp):$ | $\quad$ the uniqueness in (A) of Problem 9.28 is denied. |
