Consider a particle with the mass $m$ in the box
(i.e.,
the closed interval $[0,2]$)
in the one dimensional space
${\mathbb R}$.
The motion of this particle
(i.e.,
the wave function of the particle)
is represented by
the following Schrödinger equation
where
10.5: Exercise:Solve Schrödinger equation by variable separation method
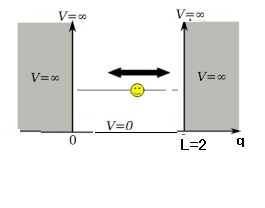
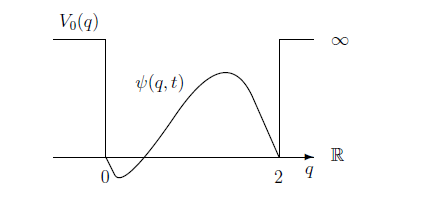
Put \begin{align} \phi(q,t) = T(t) X(q) \qquad (0 \le q \le 2). \end{align}
And consider the following equation:
\begin{align} i \hbar \frac{\partial}{\partial t } \phi (q ,t) = - \frac{\hbar^2 \partial^2}{2 m \partial q^2 }\phi (q ,t). \end{align}Then, we see
\begin{align} \frac{i T' (t) }{T(t)} =- \frac{ X'' (q)}{2 m X(q) } = K (= \mbox{ constant }). \end{align}Then,
\begin{align} \phi (q, t) = T(t)X(q) = C_3 \exp (iKt) \Big(C_1 \exp(i \sqrt{2mK/\hbar} \; q) + C_2 \exp(-i \sqrt{2mK/\hbar} \; q). \Big) \end{align}Since $X(0)=X(2)=0$ (perfectly elastic collision), putting $K= \frac{n^2 \pi^2 \hbar}{8 m}$, we see
\begin{align} \phi (q, t) = T(t)X(q) = C_3 \exp (\frac{ i n^2 \pi^2 \hbar t}{8 m}) \sin(n \pi q / 2) \qquad (n=1,2,...). \end{align}Assume the initial condition:
\begin{align} \psi(q,0) = c_1 \sin (\pi q / 2) + c_2 \sin (2 \pi q / 2) + c_3 \sin (3 \pi q / 2) + \cdots. \end{align}where $\int_{\mathbb R} | \psi(q , 0)|^2 dq = 1$. Then we see
\begin{align} & \psi(q,t) \\ = & c_1 \exp (\frac{ i \pi^2 \hbar t}{8 m}) \sin (\pi q / 2) + c_2 \exp (\frac{ i 4 \pi^2 \hbar t}{8 m}) \sin (2 \pi q / 2) + c_3 \exp (\frac{ i 9 \pi^2 \hbar t}{8 m}) \sin (3 \pi q / 2) + \cdots. \end{align}
And thus, we have the time evolution of the state
by
