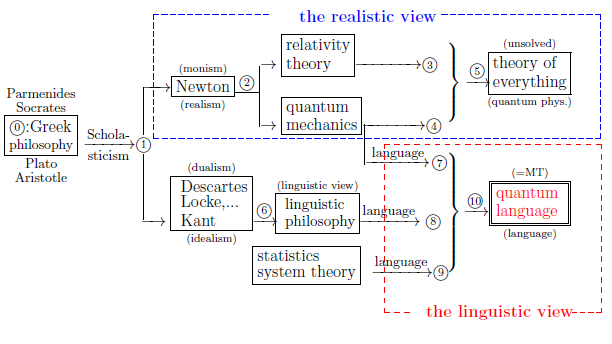
The problems
("What is space?" and "What is time?")
are the most important in
modern science as well as the traditional philosophies.
In this section, we give my answer to this problem.
10.7.1: "What is space?" and "What is time?"
10.7: Leibniz=Clarke Correspondence: What is space-time?
This section is published in the followings
$\bullet$ S. Ishikawa: "Leibniz-Clarke Correspondence, Brain in a Vat, Five-Minute Hypothesis, McTaggart’s Paradox, etc. Are Clarified in Quantum Language"Open Journal of philosophy, Vo.8 No.5 2018, 466-480 (PDF download free), $\bullet$ S. Ishikawa: "Leibniz-Clarke Correspondence, Brain in a Vat, Five-Minute Hypothesis, McTaggart’s Paradox, etc. Are Clarified in Quantum Language [Revised version]"Reseach Report ( Dept. Math. Keio Univ.) KSTS/RR-18/001
Or,
Revised Version; Pilpapers (PDF download free)
10.7.1.1: Space in quantum language ( How to describe "space" in quantum language)

In what follows, let us explain "space" in measurement theory (= quantum language ). For example, consider the simplest case, that is,
| $(A):$ | $ \qquad \qquad \mbox{"space"=${\mathbb R}_q$( one dimensional space)} $ |
| $(B):$ | $ \left\{\begin{array}{ll} \mbox{(B$_1$): a classical particle in the one dimensional space ${\mathbb R}_q$} \\ \\ \mbox{(B$_2$): a quantum particle in the one dimensional space ${\mathbb R}_q$} \end{array}\right. $ |
In the classical case, we start from the following state:
\begin{align} \mbox{ $(q,p)$ $=$ ("position", "momentum") $\in {{\mathbb R}_q \times {\mathbb R}_p }$ } \end{align}Thus, we have the classical basic structure:
| $(C_1):$ | $ \qquad [ C_0({\mathbb R}_q \times {\mathbb R}_p) \subseteq L^\infty ( {\mathbb R}_q \times {\mathbb R}_p) \subseteq B( L^2 ( {\mathbb R}_q \times {\mathbb R}_p) ] $ |
Also, concerning quantum system, we have the quantum basic structure:
| $(C_2):$ | $ \qquad [ {\mathcal C}( L^2 ( {\mathbb R}_q ) \subseteq B( L^2 ( {\mathbb R}_q ) \subseteq B( L^2 ( {\mathbb R}_q ) ] $ |
Summing up, we have the basic structure
| $(C):$ | $ [{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)] \left\{\begin{array}{ll} \mbox{(C$_1$): classical $ [ C_0({\mathbb R}_q \times {\mathbb R}_p) \subseteq L^\infty ( {\mathbb R}_q \times {\mathbb R}_p) \subseteq B( L^2 ( {\mathbb R}_q \times {\mathbb R}_p) ] $ } \\ \\ \mbox{(C$_2$): quantum $ [ {\mathcal C}( L^2 ( {\mathbb R}_q ) \subseteq B( L^2 ( {\mathbb R}_q ) \subseteq B( L^2 ( {\mathbb R}_q ) ] $} \end{array}\right. $ |
Since we always start from a basic structure in quantum language, we consider that
\begin{align} & \mbox{ How to describe "space" in quantum language} \nonumber \\ \Leftrightarrow & \mbox{ How to describe [(A):space] by [(C):basic structure] } \tag{10.29} \end{align}This is done in the following steps.
| $(D_1):$ | Begin with the basic structure:
\begin{align}
[{\mathcal A} \subseteq \overline{\mathcal A}
\subseteq
B(H)]
\end{align}
|
| $(D_2):$ |
Next, consider a certain commutative $C^*$-algebra ${\mathcal A}_0
(=C_0(\Omega ))$
such that
\begin{align}
{\mathcal A}_0 \subseteq \overline{\mathcal A}
\end{align}
|
| $(D_3):$ | Lastly, the spectrum $\Omega$ $(\approx {\frak S}^p ({\mathcal A}_* ) )$ is used to represent "space". |
| $(E_1):$ |
in the classical case (C$_1$):
\begin{align}
[
C_0({\mathbb R}_q \times {\mathbb R}_p)
\subseteq
L^\infty ( {\mathbb R}_q \times {\mathbb R}_p)
\subseteq
B(
L^2 ( {\mathbb R}_q \times {\mathbb R}_p))
]
\end{align}
we have the commutative $C_0({\mathbb R}_q )$ such that \begin{align} C_0({\mathbb R}_q ) \subseteq L^\infty ({\mathbb R}_q \times {\mathbb R}_p ) \end{align}And thus, {we get the space ${\mathbb R}_q$} as mentioned in (A) |
| $(E_2):$ |
in the quantum case (C$_2$):
\begin{align}
[
{\mathcal C}(
L^2 ( {\mathbb R}_q )
\subseteq
B(
L^2 ( {\mathbb R}_q ))
\subseteq
B(
L^2 ( {\mathbb R}_q ))
]
\end{align}
we have the commutative $C_0({\mathbb R}_q )$ such that \begin{align} C_0({\mathbb R}_q ) \subseteq B( L^2 ( {\mathbb R}_q )) \end{align}And thus, {we get the space ${\mathbb R}_q$} as mentioned in (A) |

| $(F_1):$ | Let $T$ be a tree. (Don't mind the finiteness or infinity of $T$. cf.
Chapter 14 .)
For each $t \in T$, consider the basic structure:
\begin{align}
[{\mathcal A}_t \subseteq \overline{\mathcal A}_t \subseteq B(H_t)]
\end{align}
|
| $(F_2):$ | Next, consider a certain linear subtree $T' (\subseteq T)$, which can be used to represent "time". |
10.7.2: Leibniz-Clarke Correspondence

The above argument urges us to recall Leibniz-Clarke Correspondence (1715--1716:), which is important to know both Leibniz's and Clarke's (=Newton's) ideas concerning space and time.
| $(G):$ |
[The realistic space-time]
Newton's absolutism says that the space-time should be regarded as a receptacle of a "thing." Therefore, even if "thing" does not exits, the space-time exists. |
| $(H):$ |
[The metaphysical space-time]
Leibniz's relationalism says that
|
Therefore, I regard this correspondence as \begin{align} \underset{\mbox{ (realistic view)}}{\fbox{Newton ($\approx$ Clarke)}} \quad \underset{\mbox{v.s.}}{\longleftrightarrow} \quad \underset{\mbox{ (linguistic view)}}{\fbox{Leibniz}} \end{align}
which should be compared to
\begin{align} \underset{\mbox{ (realistic view)}}{\fbox{Einstein}} \quad \underset{\mbox{v.s.}}{\longleftrightarrow} \quad \underset{\mbox{ (linguistic view)}}{\fbox{Bohr}} \end{align}
(also, recall Note 4.4).
| $\fbox{Note 10.6}$ |
Many scientists may think that
in which Newton and Leibniz respectively devotes himself to ① and ②. Although Leibniz's assertion is not clear, we believe that
|
| $\fbox{Note 10.7}$ |
I want to believe that
"realistic" vs. "linguistic"
is always hidden behind
the greatest disputes in the history of the world view.
That is,
\begin{align}
\underset{\mbox{ }}{\fbox{$\mbox{realistic world view}$}}
\quad
\underset{\mbox{v.s.}}{\longleftrightarrow}
\quad
\underset{\mbox{ (idealistic)}}{\fbox{$\mbox{linguistic world view}$}}
\end{align}
For example, 
|
| $\fbox{Note 10.8}$ |
The space-time in measuring object
is well discussed in the above.
However,
we have to say something about
"observer's time".
We conclude that
observer's time
is meaningless in measurement theory
as mentioned the linguistic interpretation
in Chap. 1.
That is,
|