Before the answer of Problem 14.11, we give the answer to the
Problem (B$_4$),
i.e.,
the dynamical system theoretical answer.
However, in order to do it,
we have to start from the formulation of dynamical system theory in what follows
14.4.2: The answer to $(B_4)$: the dynamical system theoretical answer to Zeno's paradox
Although
statistics and dynamical system theory
have no clear formulations,
as mentioned in Chapter 13,
we have the opinion that
statistics and dynamical system theory
are the same things.
At least, the following formulation
(i.e.,
the formulation of dynamical system theory in the narrow sense)
should belong to
statistics.
①:
$
\underset{\mbox{}}{\fbox{State equation}}
$
is as follows.
Let $T={\mathbb R}$
be the time axis.
For each $t ( \in T)$,
consider the state space
$\Omega_t = {\mathbb R }^n$
($n$-dimensional real space).
The
state equation (Chap. 13 (13.2))
is defined by
the following
simultaneous ordinary differential equation of the first order
②:
$
\underset{\mbox{}}{\fbox{Measurement equation}}
$
is as follows.
Consider the measured value space
$X = {\mathbb R }^m$
($m$-dimensional real space).
The
measurement equation (Chap.13 (13.2))
is defined by
where
$g(=(g_1, g_2, \cdots, g_n)): \Omega \times {\mathbb R}^2 \to X$
is the system quantity
and
$\eta_k(t)$ is a noise
($k=1,2, \cdots, m $).
Here,
$x(t)(=(x_1(t), x_2(t), \cdots, x_n(t)))$
is called a motion function.
Let $q(t)$ be the position of the flying arrow
at time $t$.
That is, consider the motion function $q(t)$.
For example, assume that
the velocity
$v_q$
[resp. $v_s$]
of the quickest [resp. slowest] runner
is equal to
$v(>0)$ [resp. ${\gamma}v \; ( 0<{\gamma}<1)$].
And further,
assume that
the position
of the quickest [resp. slowest] runner
at time $t=0$
is equal to
$0$
[resp. $a \; (>0)$].
Thus,
we can assume that
the position ${\xi (t)}$
of the quickest runner
and
the position
$\eta (t)$
of the slowest
runner
at time $t$
$( \ge 0)$
is respectively represented by
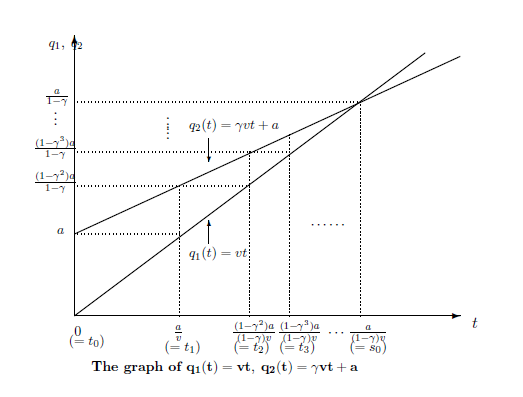
The formula (14.8) can be calculated as follows
(i.e.,
(i) or (ii)):
[(i): Algebraic calculation of (14.8)]:
Solving
$\xi(s_0)=\eta(s_0)$,
that is,
\begin{align}
vs_0 = \gamma v s_0 + a
\end{align}
we get
$s_0= \frac{a}{{(1-\gamma)} v}$.
That is,
at time
$s_0= \frac{a}{{(1-\gamma)} v}$,
the fast runner catches up with the slow runner.
[(ii): Iterative calculation of (14.8)]:
Define
$t_k$
$(k=0,1,...)$
such that,
$t_0=0$
and
Thus,
we see that
$t_k=\frac{(1-{\gamma}^k)a}{(1-{\gamma})v}$
$(k=0,1,...)$.
Then,
we have that
[(iii): Conclusion]:
After all, by the above (i)
or (ii),
we can conclude that
We of course believe that
Or equivalently,
If so,
the readers note that
Before reading Answer 14.14
(
Zeno's paradox(flying arrow)
),
confirm
our spirit:
In Corollary 14.7, putting
\begin{align}
q(t)=y_t( = g_t(\phi_{{t_0},t } (\omega_{t_0} )))
\end{align}
we get
the time-position function
$q(t)$.
Although there may be several opinions,
we consider that the followings (i.e.,
(K$_1$) and (K$_2$))
are equivalent:
Also, for the quantum linguistic space-time, see $\S$10.7
( Leibniz=Clarke correspondence).
I doubt great philosophers' opinions
concerning Zeno's paradoxes
without
Figure 14.10.
14.4 : Zeno's paradoxes---Achilles and a tortoise
In this section,
we explain our opinion
for Zeno's paradox
( the oldest paradox in science ):
that is,
\begin{align}
\mbox{
What is the meaning of Zeno's paradox?
}
\end{align}
14.4.1: What is Zeno's paradox?
Although Zeno's paradox has some types (i.e.,
"flying arrow",
"Achilles and a tortoise", "dichotomy", "stadium", etc.),
I think that
{ these are essentially the same problem}.
And I think that
the flying arrow expresses the essence of the problem exactly and is the first masterpiece in Zeno's paradoxes.
However, since "Achilles and the tortoise" may be more famous, I will also describe this
as follows.
 [Flying arrow is at rest]
[Flying arrow is at rest]
$\bullet$
Consider a flying arrow.
In any one instant of time, the arrow is at rest.
Therefore,
If the arrow is motionless at every instant, and time is entirely composed of instants, then
motion is impossible.
[Achilles and a tortoise]
$\bullet$
I consider competition of Achilles and a tortoise.
Let the start point of a tortoise (a late runner) be the front from the starting point of Achilles (a quick runner).
Suppose that both started simultaneously.
If Achilles tries to pass a tortoise, Achilles has to go to the place in which a tortoise is present now.
However, then, the tortoise should have gone ahead more.
Achilles has to go to the place in which a tortoise is present now further.
Even Achilles continues this infinite, he can never catch up with a tortoise.
In order to explain
\begin{align}
\mbox{
"What is Zeno's paradox?"
}
\end{align}
we have to start from the following Figure.
That is, we assert that
\begin{align}
\mbox{Zeno's paradox can not be understood without the following figure:}
\end{align}
However, we have the following problems:
$(A):$
Descartes=Kant philosophy and
the philosophy of language
have no power to
describe
Zeno's paradox (Paradox 14.9).
And, finally, we have
$(B_1):$
How do we describe Zeno's paradox (Paradox 14.9) in terms of Newtonian mechanics?
$(B_2):$
How do we describe Zeno's paradox (Paradox 14.9) in terms of quantum mechanics?
$(B_3):$
How do we describe Zeno's paradox (Paradox 14.9) in terms of the theory of relativity?
$(B_4):$
How do we describe Zeno's paradox (Paradox 14.9) in terms of statistics
(i.e., the dynamical system theory)
?
$(B_5):$
How do we describe Zeno's paradox (Paradox 14.9) in terms of quantum language?
We assert that
$(C):$
What is the most proper world description
for
Zeno's paradox (Paradox 14.9)?
and conclude that
$(D):$
"to solve
Zeno's paradox (Paradox 14.9)"
$\Longleftrightarrow$
"to answer the above $(B_5)$"
Therefore,
it suffices to answer the above
(B$_5$)
, that is,
$(E):$
The answer of the above (C)
is just quantum language
$\quad$
Describe "flying arrow" and
"Achilles an a tortoise"
in (classical) quantum language!
14.4.2.1: The formulation of dynamical system theory
Dynamical system theory is formulated as follows.
\begin{align}
\underset{\mbox{}}{\fbox{Dynamical system theory}}
=
\underset{\mbox{}}{\fbox{①:State equation}}
+
\underset{\mbox{}}{\fbox{②:Measurement equation}}
\tag{14.9}
\end{align}
14.4.2.2: The dynamical system theoretical answer to Zeno's paradox

Thus, Zeno's logic is wrong.
$\bullet$
Note that the following logic (i.e., Zeno's logic ) is wrong:
$\bullet$
for each time $t$, the position $q(t)$ of the flying arrow
is determined.
$\Longrightarrow$
the motion function $q$ is a constant function
[The dynamical system theoretical answer to "Achilles and a tortoise (in Paradox 14.9)"]
$\bullet$
Calculations
as $k \to \infty $.
Therefore, the quickest runner catches up with the slowest
at time $s_0 =\frac{a}{(1-{\gamma})v}$.
$(\sharp):$
the quickest runner can overtake the slowest
at time
$s_0 =\frac{a}{(1-{\gamma})v}$.
14.4.2.3: Why isn't the Answer 14.13 authorized?
We believe that
Answer 14.13
is not the wrong answer of
Zeno's paradox. If so, we have to answer the following question:
$(F):$
Why isn't the Answer 14.13 accepted as the final answer of
Zeno's paradox?
$(G_1):$
the reason is due to the fact
that
statistics
(=dynamical system theory)
is not
accepted as the world-view
in Figure 14.10
$(G_1):$
the linguistic world-view is not
accepted as the world-view
in Figure 14.10
$(H):$
the purpose of this note
is to assert that
the linguistic world view
should be authorized
in Figure 14.10.
14.4.3: Quantum linguistic answer to Zeno's paradoxes
Therefore,
$(I):$
The theory
described in ordinary language
should be described in a certain world description.
That is because
almost ambiguous problems
are due
to
the lack of
"the world-description method".
This will be done as follows.
$(J):$
it suffices to describe
"motion function $q(t)$ in Answer 14.13
(flying arrow)"
in terms of quantum language.
Here, the motion function should be a measured value, in which the causality is concealed.

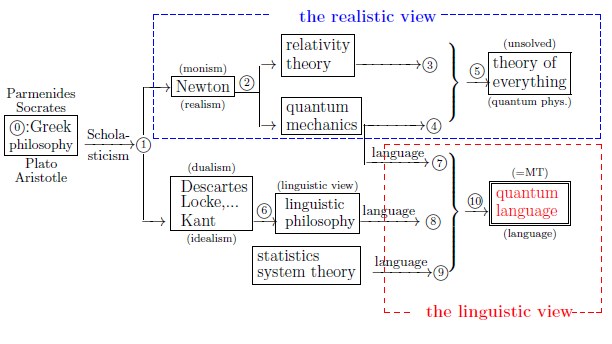
$\qquad \qquad $Fig.1.1:The history of world-descriptions
$(K_1):$
to accept Figure 14.10(=Fig.1.1):[The history of the world-view]
$(K_2):$
to believe in Answer 14.14 as the final answer of
Zeno's paradox
$\fbox{Note 14.2}$
I think that
"the flying arrow" is Zeno's best work.
If readers agree to the above answer,
they can easily answer the other Zeno's paradoxes.
Also,
it should be noted that
Zeno of Elea (BC. 490-430)
was a Greek philosopher
(about 2500 years ago).
Hence, we are not concerned with the historical aspect of Zeno's paradoxes.
Therefore,
we think that
and
$(\sharp):$
"How did Zeno think Zeno's paradoxes?"
is not important
from the scientific point of view.
$(\sharp):$
What is important is
"How do we think Zeno's paradoxes?"
14.4 : Zeno's paradoxes---Flying arrow is at rest
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
Contents:
Paradox 14.9 [Zeno's paradox]
Figure 14.10 [=Figure 1.1 in $\S$1.1:
The location of quantum language in the history of world-description]
Fig.1.1: the location of "quantum language" in the world-views
It is clear that
Problem 14.11 [The meaning of Zeno's paradox]
Formulation 14.12 [The formulation of dynamical system theory in the narrow sense]
Answer 14.13[The dynamical system theoretical answer to "flying arrow (in Paradox 14.9)"]
Answer 14.14 [The answer to Problem14.11 ]
or
[Answer to Problem 14.9: Zeno's paradox(flying arrow)]
