19.2: The principle of equal odds weight
From the above arguments, we see that
Proclaim 19.4 [The principle of equal weight]
Consider a finite state space $\Omega$
with the discrete metric,
that is,
$\Omega=\{\omega_1,\omega_2,\ldots,$
$\omega_n\}$.
Let
${\mathsf O}=(X, {\cal F}, F)$
be an observable in
$C_{} (\Omega)$.
Consider a measurement
$
{\mathsf M}_{C_{} (\Omega )}({\mathsf O} ,
S_{[
\ast]}
)
$.
If the observer has no information for the unknown state
$[\ast]$,
there is a reason to
assume
that
this measurement is also represented by
the mixed measurement
$
{\mathsf M}_{C_{} (\Omega )}({\mathsf O} ,
S_{[
\ast]}(\rho_{\scriptsize{\mbox{prior}}})
)
$,
where
\begin{align}
\rho_{\scriptsize{\mbox{prior}}}
= \frac{1}{n} \sum_{k=1}^n \delta_{\omega_k}
\tag{19.9}
\end{align}
Explanation
In betting,
it is certain that
everybody wants to choose
an
unpopular $\omega_k$.
Thus,
I believe that nobody disagrees with Proclaim 19.4.
Also, it should be noted that
| $(J):$ |
the term
"probability"
can be freely used within the rule of Axiom 1 or
Axiom$^{(m)}$ 1.
|
 The reason that the justice
of the (B)
is not assured yet
is due to the lack of the understanding of the (J).
The reason that the justice
of the (B)
is not assured yet
is due to the lack of the understanding of the (J).
| $\fbox{Note 19.1}$ | In this book, we deal with three
"the principle of equal weight" as follows:
| $(\sharp_1):$ |
"the principle of equal weight" in Remark 5.19 ($\S$5.6)
|
| $(\sharp_2):$ |
"the principle of equal weight" in Theorem 9.18 ($\S$9.7)
|
| $(\sharp_3):$ |
"the principle of equal weight" in Proclaim 19.4 ($\S$19.2)
|
|
Problem 19.5 [Monty Hall problem; Problem 5.14 ;The principle of equal weight]
You are on a game show and you are given the choice of three doors.
Behind one door is a car, and behind the other two are goats.
You choose, say, door 1, and the host, who knows where the car is,
opens another door,
behind which is a goat.
For example,
the host says that
| $(\flat):$ |
the door 3 has a goat.
|
And further,
he now gives you the choice of
sticking with door 1 or switching to door 2?
What should you do?
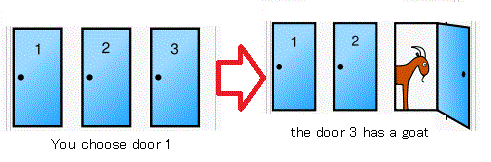 Figure 19.6:
Monty Hall problem
Figure 19.6:
Monty Hall problem
Proof
It should be noted that
the above is completely the same as
Problem 5.14.
However,
the proof
is different.
That is,
it suffices to use
Proclaim 19.4
and
Bayes theorem
(B$_2$).
That is, the proof is similar to
Problem
9.16.
$\square \quad$


