20.2: The summary of quantum language
$(C_1)$
$
\underset{\mbox{ (=quantum language)}}{\fbox{pure measurement theory (A)}}
:=
\underbrace{
\underset{\mbox{ (\(\S\)2.7)}}{
\overset{
[\mbox{ (pure) Axiom 1}]
}{\fbox{pure measurement}}
}
+
\underset{\mbox{ ( \(\S \)10.3)}}{
\overset{
[{\mbox{ Axiom 2}}]
}{\fbox{Causality}}
}
}_{\mbox{ a kind of incantation (a priori judgment)}}
+
\underbrace{
\underset{\mbox{
(\(\S\)3.1)
}}
{
\overset{
{}}{\fbox{Linguistic interpretation}}
}
}_{\mbox{ the manual on how to use spells}}
$
$(C_2)$
$
\underset{\mbox{ (=quantum language)}}{\fbox{mixed measurement theory (A)}}
:=
\underbrace{
\color{red}{
\underset{\mbox{ (\(\S\)9.1)}}{
\overset{
[\mbox{ (mixed) Axiom 1}]
}{\fbox{mixed measurement}}
}
}
+
\underset{\mbox{ ( \(\S \)10.3)}}{
\overset{
[{\mbox{ Axiom 2}}]
}{\fbox{Causality}}
}
}_{\mbox{ a kind of incantation (a priori judgment)}}
+
\underbrace{
\underset{\mbox{
(\(\S\)3.1)
}}
{
\overset{
{}}{\fbox{Linguistic interpretation}}
}
}_{\mbox{ the manual on how to use spells}}
$
20.2.1: The big-picture view of quantum language
And the structure is as follows.
In this chapter,
we will study {"Axiom${}^{(m)}$ 1(mixed measurement)"} in mixed measurement theory,
that is,
$(B):$
$
\underset{(=\mbox{ quantum language})}{\mbox{measurement theory}}
\left\{\begin{array}{ll}
\underset{\mbox{($\sharp_1$)}}{
\mbox{pure type}}
\left\{\begin{array}{ll}
\!\!
\mbox{classical system}
:
\mbox{ Fisher statistics}
\\
\!\!
\mbox{ quantum system}
:
\mbox{
usual quantum mechanics
}
\\
\end{array}\right.
\\
\\
\underset{\mbox{($\sharp_2$)}}
{\mbox{mixed type}}
\left\{\begin{array}{ll}
\!\!
\mbox{ classical system}
:
\mbox{including Bayesian statistics, }\\
\qquad \qquad \mbox{Kalman filter}
\\
\!\!
\mbox{ quantum system}
:
\mbox{ quantum decoherence
}
\\
\end{array}\right.
\end{array}\right.
$
In the above,
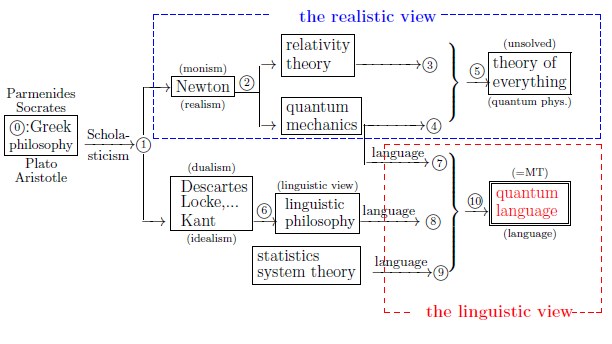
$\qquad \qquad $Fig.1.1: The history of world-descriptions
On the other hand,
the linguistic interpretation
(i.e.,
the manual on how to use Axioms 1 and 2)
may not be indispensable. However,
$(D_1):$
Axioms 1 and 2 (i.e., kinds of spells) are essential
In this sense, this note is a manual book
(=cookbook).
Although
all written in this note can be regarded as a part of the linguistic interpretation,
the most important statement is
$(D_2):$
if we would like to make speed of acquisition of a quantum language as quick as possible, we may want the good manual on how to use the axioms.
$(E):$
Many philosophers' maxims and thoughts constitute a part of the linguistic interpretation
Also, we see:
The characteristic of quantum language
$(F_1):$
Non-reality (metaphysics ):
Quantum language is metaphysics
(= language),
which asserts the linguistic world-view.
$(F_2):$
The collapse of wave function does not occur:
According to the linguistic interpretation
(i.e.,
only one measurement is permitted),
we can not get information after the measurement.
That is,
the collapse of wave function
can not be found,
However, in the sense of "Projection postulate 11.6 ( in Section 11 )", the collapse of wave function is accepted in
the linguistic interpretation.
$(F_3):$
Non-deterministic:
Since we usually consider non-deterministic processes in classical system,
it is natural to assume non-deterministic processes
(i.e.,
quantum decoherence)
in quantum language.

$(F_4):$
Dualism:
The two concepts:
"measurement" and "dualism" are non-separable.
Thus, quantum language say that
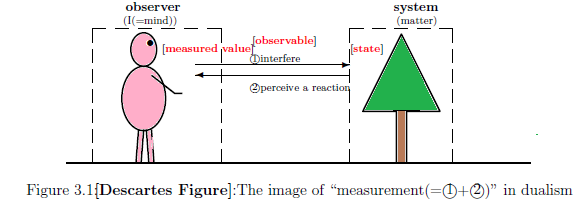
$(F_5):$
Non-locality, faster-than-light:
Quantum language accepts "non-locality".
This is the only one paradox in quantum language.
$(F_6):$
Many paradoxes and unsolved problems are clarified
$(a):$

Paradoxes and unsolved problems due to a lack of quantum language:
What is probability (causality, space-time) ?
Zeno's paradox, the principle of equal probability,
classical syllogizm, classical Bell's inequlity
$(b):$
Paradoxes and unsolved problems solved by descriptive power
of quantum language:
Schr\"odinger's cat
$(c):$
What we cannot speak about we must pass over in silence:
Heisenberg's uncertainty principle (due to
the thought experiment by
$\gamma$-ray microscope),
Cogit proposition, Wigner's friend, delayed choice experiment
$(d):$
Everything should be spoken by quantum language:
Several problems in statistics (Fisher's maximum likelihood method,
Bayes method,
semi-distance (confidence interval, statistical hypothesis, ANOVA),
regression analysis,
Kalman filter)
20.2: The summary of quantum language
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
The big-picture view of quantum language
Measurement theory
(= quantum language ) is classified as follows.
Only one measurement is permitted
Also,since we assert that quantum language is the final goal of
dualistic idealism
(=
Descartes=Kant philosophy) in Figure20.1, we think that
20.2.2 The characteristic of quantum language
