たとえば、次のことを考える。

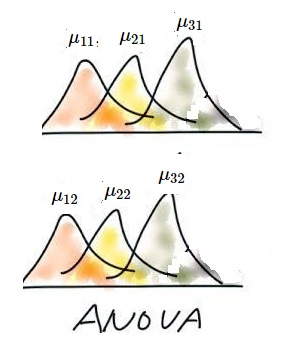
$(\sharp_{11})$ $x_{111}, x_{112}, x_{113},..., x_{11n}$ は正規分布$N(\mu_{11}, \sigma)$から得られたデータ
$(\sharp_{21})$ $x_{211}, x_{212}, x_{213},..., x_{21n}$ は正規分布$N(\mu_{21}, \sigma)$から得られたデータ
$(\sharp_{31})$ $x_{311}, x_{312}, x_{313},..., x_{31n}$ は正規分布$N(\mu_{31}, \sigma)$から得られたデータ
$(\sharp_{12})$ $x_{121}, x_{122}, x_{123},..., x_{12n}$ は正規分布$N(\mu_{12}, \sigma)$から得られたデータ
$(\sharp_{22})$ $x_{221}, x_{222}, x_{223},..., x_{22n}$ は正規分布$N(\mu_{22}, \sigma)$から得られたデータ
$(\sharp_{32})$ $x_{321}, x_{322}, x_{323},..., x_{32n}$ は正規分布$N(\mu_{32}, \sigma)$から得られたデータ
と仮定しよう。 このとき、
  • データ$(\sharp_{11})-(\sharp_{32})$ から、
    \begin{align} & \mu_{ij} -\frac{\mu_{i1}+\mu_{i2}}{2} -\frac{\mu_{1j}+\mu_{2j}+\mu_{3j}}{3} + \frac{\mu_{11}+\mu_{12}+\mu_{13} +\mu_{21}+\mu_{22}+\mu_{23} }{6} = 0 \\ & \quad \qquad \qquad (i=1,2, j=1,2,3) \end{align} の可能性は少ない
    と結論するには、 如何なる議論が可能か？
を考えたい。 これが、 二元配置分散分析(II) で以下に説明する。

$\S$7.3.4 帰無仮説:$\quad (\alpha \beta)_{ij}=0$ ($\forall i=1,2, \ldots, a,\;j=1,2, \ldots, b$ )

さて, \begin{align} \Theta = {\mathbb R}^{ab} \tag{7.50} \end{align}

そして, システム量$\pi : \Omega \to \Theta $ を次のように定める.

\begin{align} & \small{ \Omega = {\mathbb R}^{ab} \times {\mathbb R}_+ \ni \omega =( (\mu_{ij})_{i=1,2, \ldots, a,\;\;j=1,2, \ldots, b } , \sigma) \mapsto \pi(\omega) = ((\alpha \beta)_{ij})_{i=1,2, \ldots, a,\;\;j=1,2, \ldots, b } \in \Theta = {\mathbb R}^{ab} } \\ & \tag{7.51} \end{align} ここで,以下を思い出そう. \begin{align} (\alpha \beta)_{ij} =\mu_{ij}-\mu_{i \bullet} -\mu_{\bullet j }+\mu_{\bullet \bullet } \tag{7.52} \end{align}

また,推定量 $E: X(={\mathbb R}^{abn}) \to \Theta(={\mathbb R}^{ab} )$ を次のように定める. \begin{align} & E( (x_{ijk})_{i=1,...,a, \; j=1,2,...b, \; k=1,2,...,n }) \nonumber \\ = & \Big(\frac{ \sum_{k=1}^n x_{ijk}}{n} - \frac{ \sum_{j=1}^b \sum_{k=1}^n x_{ijk}}{bn} - \frac{ \sum_{j=1}^b\sum_{k=1}^n x_{ijk}}{an} + \frac{\sum_{i=1}^a \sum_{j=1}^b \sum_{k=1}^n x_{ijk}}{abn} \Big)_{i=1,2,\ldots, a \; j=1,2,...b, } \nonumber \\ = & \Big( x_{i j \bullet } - x_{i \bullet \bullet } - x_{\bullet j \bullet } + x_{\bullet \bullet \bullet } \Big)_{i=1,2,\ldots, a \; j=1,2,...b,} \tag{7.53} \end{align}



我々の問題は,以下の通りである.

問題7.5[二元配置分散分析]

並行同時正規測定 \begin{align*} {\mathsf M}_{L^\infty ({\mathbb R}^{ab} \times {\mathbb R}_+ )} ( {\mathsf O}_G^{{{abn}}} = (X(\equiv {\mathbb R}^{{{abn}}}), {\mathcal B}_{\mathbb R}^{{{abn}}}, {{{G}}^{{{abn}}}} ), S_{[(\mu=(\mu_{ij}\;|\; i=1,2,\cdots, a, j=1,2,\cdots,b ), \sigma )]} ) \end{align*} を考えよう. 帰無仮説 $H_N ( \subseteq \Theta = {\mathbb R}^{ab})$ を次のように定める. \begin{align} H_N & \small{ = \{ ((\alpha \beta)_{ij})_{i=1,2, \ldots, a,\;\;j=1,2, \ldots, b } \in \Theta = {\mathbb R}^{ab} \;:\; (\alpha \beta)_{ij}=0, (\forall {i=1,2, \ldots, a,\;\;j=1,2, \ldots, b } ) \} } \\ & \tag{7.54} \end{align} すなわち \begin{align} (\alpha \beta)_{ij} =\mu_{ij}-\mu_{i \bullet} -\mu_{\bullet j }+\mu_{\bullet \bullet }=0 \quad (i=1,2, \cdots, a, \quad j=1,2, \cdots,b ) \tag{7.55} \end{align} を仮定する.　$0 < \alpha \ll 1$とする. このとき,次を満たす${\widehat R}_{{H_N}}^{\alpha; \Theta}( \subseteq \Theta)$で,「出来るだけ大きいもの(しかも,$\sigma$に依存しないもの)」を見つけよ

$(D_1):$ $ {\mathsf M}_{L^\infty ({\mathbb R}^{ab} \times {\mathbb R}_+ )} ( {\mathsf O}_G^{{{abn}}} = (X(\equiv {\mathbb R}^{{{abn}}}), {\mathcal B}_{\mathbb R}^{{{abn}}}, {{{G}}^{{{abn}}}} ), S_{[(\mu=(\mu_{ij}\;|\; i=1,2,\cdots, a, j=1,2,\cdots,b ), \sigma )]} ) $ の測定値$x(\in{\mathbb R}^{abn} )$が, \begin{align*} E(x) \in {\widehat R}_{{H_N}}^{\alpha; \Theta} \end{align*} を満たす確率は,$\alpha$以下である.

解答.

さて, \begin{align} & \| \theta^{(1)}- \theta^{(2)} \|_\Theta = \sqrt{ \sum_{i=1}^a \sum_{j=1}^b \Big(\theta_{ij}^{(\ell)} - \theta_{ij}^{(\ell)} \Big)^2 } \tag{7.56} \\ & \qquad (\forall \theta^{(\ell)} =( \theta_{ij}^{(\ell)})_{i=1,2, \ldots, a,\;\;j=1,2, \ldots, b } \in {\mathbb R}^{ab}, \; \ell=1,2 ) \nonumber \end{align}


として, 半距離 $d_\Theta^x$ in $\Theta$ を次のように定める.

\begin{align} & d_\Theta^x (\theta^{(1)}, \theta^{(2)}) = \frac{\|\theta^{(1)}- \theta^{(2)} \|_\Theta}{ \sqrt{{\overline{SS}}(x)} } \qquad (\forall \theta^{(1)}, \theta^{(2)} \in \Theta, \forall x \in X ) \tag{7.57} \end{align}

さて,

\begin{align} & E( (x_{ijk}-\mu_{ij})_{i=1,...,a, \; j=1,2,...b, \; k=1,2,...,n }) \nonumber \\ = & \Big(\frac{ \sum_{k=1}^n (x_{ijk}-\mu_{ij})}{n} - \frac{ \sum_{j=1}^b \sum_{k=1}^n (x_{ijk}-\mu_{ij})}{bn} \nonumber \\ & \qquad - \frac{ \sum_{j=1}^b\sum_{k=1}^n (x_{ijk}-\mu_{ij})}{an} + \frac{\sum_{i=1}^a \sum_{j=1}^b \sum_{k=1}^n (x_{ijk}-\mu_{ij})}{abn} \Big)_{i=1,2,\ldots,\; j=1,2,...b, } \nonumber \\ = & \Big( (x_{i j \bullet} - \mu_{ij}) - (x_{i \bullet \bullet }-\mu_{i \bullet}) - (x_{\bullet j \bullet }- \mu_{\bullet j}) + (x_{\bullet \bullet \bullet }- \mu_{\bullet \bullet }) \Big)_{i=1,2,\ldots,\; j=1,2,...b,} \nonumber \\ = & \Big( x_{i j \bullet } - x_{i \bullet \bullet } - x_{\bullet j \bullet } + x_{\bullet \bullet \bullet } \Big)_{i=1,2,\ldots,\; j=1,2,...b} \qquad (\mbox{注意:帰無仮説 }(\alpha \beta)_{ij}=0 ) \\ & \tag{7.58} \end{align} したがって, \begin{align} E( (x_{ijk})_{i=1,...,a, \; j=1,2,...b, \; k=1,2,...,n }) = E( (x_{ijk}-\mu_{ij})_{i=1,...,a, \; j=1,2,...b, \; k=1,2,...,n }) \tag{7.59} \end{align}

よって, 各 $i=1,...,a, \; j=1,2,...b,$

\begin{align} & E_{ij} (x_{ijk} -\mu_{ij}) \nonumber \\ = & \frac{ \sum_{k=1}^n (x_{ijk}-\mu_{ij})}{n} - \frac{ \sum_{j=1}^b \sum_{k=1}^n (x_{ijk}-\mu_{ij})}{bn} - \frac{ \sum_{j=1}^b\sum_{k=1}^n (x_{ijk}-\mu_{ij})}{an} \nonumber \\ & \qquad \qquad + \frac{\sum_{i=1}^a \sum_{j=1}^b \sum_{k=1}^n(x_{ijk}-\mu_{ij})}{abn} \nonumber \\ = & E_{ij}(x)- (\alpha\beta)_{ij} \nonumber \\ = & x_{i j \bullet } - x_{i \bullet \bullet } - x_{\bullet j \bullet } + x_{\bullet \bullet \bullet } - (\alpha\beta)_{ij} \tag{7.60} \end{align}

そして,　次を得る. \begin{align} & \| E(x) - \pi (\omega )\|^2_\Theta \nonumber \\ = & || \Big( E_{ij}(x) - (\alpha \beta)_{ij} \Big)_{i=1,2,\ldots,\; j=1,2,...b } ||_\Theta^2 \tag{7.61} \end{align}

帰無仮説 $H_N$ (i.e., $(\alpha \beta)_{ij}=0$ $(\forall i=1,2,\ldots, a, \; j=1,2, \ldots, b )$ )に注意して,

\begin{align} = & \sum_{i=1}^a\sum_{j=1}^b( x_{i j \bullet } - x_{i \bullet \bullet } - x_{\bullet j \bullet } + x_{\bullet \bullet \bullet } )^2 \tag{7.62} \end{align}



よって, 任意の $ \omega=(\mu, \sigma ) ({}\in \Omega= {\mathbb R}^{ab} \times {\mathbb R} )$に対して, 正数 $\eta^\alpha_{\omega}$ $({}> 0)$ を次のように定める.

\begin{align} \eta^\alpha_{\omega} = \inf \{ \eta > 0: [G(E^{-1} ( {{ Ball}^C_{d_\Theta^{x}}}(\pi(\omega) ; \eta))](\omega ) \ge \alpha \} \tag{7.63} \end{align}



帰無仮説$H_N$ (i.e., $(\alpha \beta)_{ij}=0$ $(\forall i=1,2,\ldots, a, \; j=1,2, \ldots, b )$ )を考慮して,$\eta^\alpha_{\omega}$を計算すると,

\begin{align} & E^{-1}({{ Ball}^C_{d_\Theta^{x} }}(\pi(\omega) ; \eta )) =\{ x \in X = {\mathbb R}^{abn} \;:\; d_\Theta^x (E(x), \pi(\omega )) > \eta \} \nonumber \\ = & \{ x \in X = {\mathbb R}^{abn} \;:\; \frac{ abn \sum_{i=1}^a\sum_{j=1}^b( x_{i j \bullet } - x_{i \bullet \bullet } - x_{\bullet j \bullet } + x_{\bullet \bullet \bullet } )^2 }{ \sum_{i=1}^a \sum_{j=1}^b\sum_{k=1}^n (x_{ijk} - x_{ij \bullet})^2 } > \eta^2 \} \tag{7.64} \end{align}



すなわち, $\pi( \omega )\in H_N (\subseteq {\mathbb R}^{ab} ) $ (i.e., $(\alpha \beta)_{ij}=0$ $(\forall i=1,2,\ldots, a, \; j=1,2, \ldots, b )$ ) を満たす 任意の状態$\omega =((\mu_{ij})_{i=1,2,\ldots,a, \;j=1,2,\ldots,b},\;, \sigma) \in \Omega ={\mathbb R}^{ab } \times {\mathbb R}_{+}$に対して, 以下の計算を得る.

\begin{align} & [{{{G}}}^{abn} ( E^{-1}({{ Ball}^C_{d_\Theta^{x} }}(\pi(\omega) ; \eta )) ) (\omega) \nonumber \\ = & \frac{1} {({ {\sqrt{2 \pi } \sigma} })^{abn}} \underset{ E^{-1}({{ Ball}^C_{d_\Theta^{x} }}(\pi(\omega) ; \eta )) } {\int \cdots \int} \exp[- \frac{ \sum_{i=1}^a \sum_{j=1}^b \sum_{k=1}^n (x_{ijk} - \mu_{ij} )^2 }{2 \sigma^2} ] \times_{k=1}^n \times_{j=1}^b \times_{i=1}^a d{x_{ijk} } \nonumber \\ = & \frac{1} {({ {\sqrt{2 \pi } \sigma} })^{abn}} \underset{ \{x \in X \;:\; d_\Theta^x ( E(x), \pi(\omega ) \ge \eta \} } {\int \cdots \int} \exp[- \frac{ \sum_{i=1}^a \sum_{j=1}^b \sum_{k=1}^n (x_{ijk} - \mu_{ij} )^2 }{2 \sigma^2} ] \times_{k=1}^n \times_{j=1}^b \times_{i=1}^a d{x_{ijk} } \nonumber \\ = & \frac{1} {({ {\sqrt{2 \pi }} })^{abn}} \underset{ \frac{ \sum_{i=1}^a\sum_{j=1}^b( x_{i j \bullet } - x_{i \bullet \bullet } - x_{\bullet j \bullet } + x_{\bullet \bullet \bullet } )^2 }{ \sum_{i=1}^a \sum_{j=1}^b\sum_{k=1}^n (x_{ijk} - x_{ij \bullet})^2 } > \frac{\eta^2}{abn} } {\int \cdots \int} \exp[- \frac{ \sum_{i=1}^a \sum_{j=1}^b \sum_{k=1}^n (x_{ijk} )^2 }{2} ] \times_{k=1}^n \times_{j=1}^b \times_{i=1}^a d{x_{ijk} } \nonumber \\ = & \frac{1} {({ {\sqrt{2 \pi }} })^{abn}} \underset{ \frac{ \frac{ \sum_{i=1}^a\sum_{j=1}^b( x_{i j \bullet } - x_{i \bullet \bullet } - x_{\bullet j \bullet } + x_{\bullet \bullet \bullet } )^2}{(a-1)(b-1)} }{ \frac{\sum_{i=1}^a \sum_{j=1}^b\sum_{k=1}^n (x_{ijk} - x_{ij \bullet})^2}{ ab(n-1) } } > \frac{\eta^2(ab(n-1))}{abn(a-1)(b-1)} } {\int \cdots \int} \exp[- \frac{ \sum_{i=1}^a \sum_{j=1}^b \sum_{k=1}^n (x_{ijk} )^2 }{2} ] \times_{k=1}^n \times_{j=1}^b \times_{i=1}^a d{x_{ijk} } \\ & \tag{7.65} \end{align}
$(D_2):$ここで, ガウス積分の公式7.8(D)(in $\S$7.4))によって,次を得る,
\begin{align} = & \int^{\infty}_{\frac{\eta^2 (n-1)}{n (a-1)(b-1)}} p_{((a-1)(b-1),ab(n-1)) }^F (t) dt =\alpha (\mbox{ e.g., } \alpha=0.05) \tag{7.66} \end{align}

ここに, $p_{((a-1)(b-1),ab({{n}}-1)) }^F$ は自由度$((a-1)(b-1),ab(n-1)) $の$F$-分布の確率密度関数である.

ここまでくれば,前の議論と同様に, 次の方程式を解けばよい.

\begin{align} {\frac{\eta^2 (n-1)}{n (a-1)(b-1)}} ={F_{ab(n-1), \alpha}^{(a-1)(b-1)} } (=\mbox{"$\alpha$-point"}) \tag{7.67} \end{align} よって、 \begin{align} (\eta^\alpha_{\omega})^2 = {F_{ab(n-1), \alpha}^{(a-1)(b-1)} } n(a-1)(b-1)/(n-1) \tag{7.68} \end{align}


したがって, 次のような棄却域${\widehat R}_{\widehat{x}}^{\alpha; \Theta}$ (or, ${\widehat R}_{\widehat{x}}^{\alpha; X}$; $H_N =\{((\alpha \beta)_{ij})_{i=1,2, \cdots, a, j=1,2, \cdots, b} \; :\; (\alpha \beta)_{ij}=0 \; (i=1,2, \cdots, a, j=1,2, \cdots, b)\}( \subseteq \Theta= {\mathbb R}^{ab})$ の $({}\alpha{})$-棄却域 ) を得る.

\begin{align} {\widehat R}_{{H_N}}^{\alpha; \Theta} & = \bigcap_{\omega =((\mu_{ij})_{i=1}^a{}_{j=1}^b, \sigma ) \in \Omega (={\mathbb R}^a \times {\mathbb R}_+ ) \mbox{ such that } \pi(\omega)= (\alpha \beta)_{ij} \in {H_N}} \{ E({x}) (\in \Theta) : d_\Theta^{x} (E({x}), \pi(\omega)) \ge \eta^\alpha_{\omega } \} \nonumber \\ & = \{ E({x}) (\in \Theta) : \frac{ (\sum_{i=1}^a \sum_{j=1}^b( x_{ij \bullet} - x_{\bullet \bullet \bullet} )^2)/((a-1)(b-1))}{ (\sum_{i=1}^a \sum_{j=1}^b\sum_{k=1}^n (x_{ijk} - x_{ij \bullet})^2) /(ab(n-1)) } \ge {F_{ab(n-1), \alpha}^{(a-1)(b-1)} } \} \tag{7.69} \end{align} また, \begin{align} & {\widehat R}_{{H_N}}^{\alpha; X}= E^{-1}({\widehat R}_{{H_N}}^{\alpha; \Theta}) = \{ x (\in X) : \frac{ (\sum_{i=1}^a \sum_{j=1}^b( x_{ij \bullet} - x_{\bullet \bullet \bullet} )^2)/((a-1)(b-1))}{ (\sum_{i=1}^a \sum_{j=1}^b\sum_{k=1}^n (x_{ijk} - x_{ij \bullet})^2) /(ab(n-1)) } \ge {F_{ab(n-1), \alpha}^{(a-1)(b-1)} } \} \\ & \tag{7.70} \end{align}

$\fbox{注釈7.4}$ 上の議論で,多少なりとも数学を使った部分(計算した部分)があるとしたら, (D$_2$)のガウス積分の公式だけであることに注意しよう.