Summing up the arguments in Chap 1, we see:

Summary ( All of quantum language ) Quantum language (= measurement theory ) is formulated as follows. \begin{align} & \underset{\mbox{ (=quantum language)}}{\fbox{pure measurement theory (A)}} := \underbrace{ \underset{\mbox{ ($\S$2.7)}}{ \overset{ [\mbox{ (pure) Axiom 1}] }{\fbox{pure measurement}} } + \underset{\mbox{ ($\S$10.3)}}{ \overset{ [{\mbox{ Axiom 2}}] }{\fbox{Causality}} } }_{\mbox{ a kind of incantation (a priori judgment)}} + \underbrace{ \underset{\mbox{ ($\S$3.1) }} { \overset{ {}}{\fbox{Linguistic interpretation}} } }_{\mbox{ the manual on how to use spells}} \label{eq1.2} \end{align}
[Axioms] Here
(A):
$\qquad \qquad $The history of world-descriptions
Axioms 1 and 2 are kinds of spells, (i.e., incantation, magic words, metaphysical statements), and thus, it is impossible to verify them experimentally. In this sense, I consider that

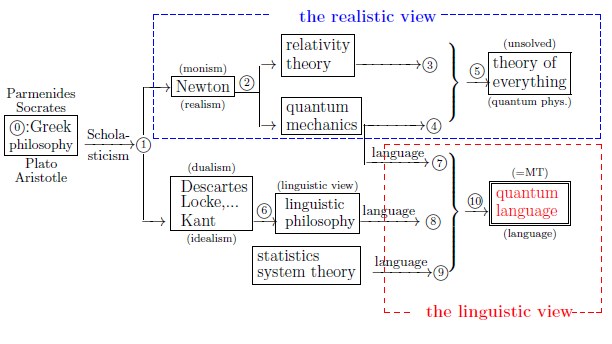
$ \underset{\mbox{(Kant philosophy)}}{\fbox{a priori synthetic judgment}} \quad \xrightarrow[\mbox{quantization}]{} \quad \underset{\mbox{(quantum language)}}{\fbox{Axioms 1 and 2}} $

which (i.e., ⑥$\rightarrow$⑧$\rightarrow$⑩ ) is realized in the right figure(i.e., the history of world-descriptions ). Therefore, what we should do is not "to understand" but "to use". After learning Axioms 1 and 2 by rote, we have to improve how to use them through trial and error.
[The linguistic interpretation] From the pure theoretical point of view, we do well without the interpretation. However,
(B): it is better to know the linguistic interpretation of quantum mechanics (= the manual on how to use Axioms 1 and 2), if we would like to make progress quantum language early.
The most important statement in the linguistic interpretation ($\S$3.1) is
Only one measurement is permitted
After all, I want to assert that \begin{align} \underset{\mbox{[dualistic idealism]}}{\mbox{Descartes philosophy}}\longrightarrow \left\{\begin{array}{ll} \color{blue}{\underset{\mbox{[Axioms]}}{\mbox{Continental Rationalism}}} \\ \\ \color{red}{\underset{\mbox{[Linguistic interpretation]}}{\mbox{British empiricism}}} \end{array}\right\} \longrightarrow \underset{\mbox{[quantum language]}}{\mbox{Kant philosophy}} \end{align}
That is, the spirit of quantum language is
In the beginning was the language!
or Wittgenstein's saying:
The limit of my language means the limit of my world
The above is everything of quantum language.