Axioms 1 and 2 (mentioned in the previous section ) are too abstract to use quantum language in real situations. So, let me show a simple example. What you will see in the following chapters is

[The measurement of "Cold or Hot" for the water in a cup] (The following can be read without the knowledge of quantum language) Let testees drink water with various temperature \( \omega ℃ (0 {{\; \leqq \;}}\omega {{\; \leqq \;}}100)\). And assume: you ask them "Cold or Hot ?" alternatively. Gather the data, ( for example, $g_{c}(\omega)$ persons say "Cold", \(g_{h}(\omega)\) persons say "Hot") and normalize them, that is, get the polygonal lines such that \begin{align*} & f_{c}(\omega)= \frac{g_{c}(\omega)}{\mbox{the numbers of testees}} \nonumber \\ &f_{h}(\omega)=\frac{g_{h}(\omega)}{\mbox{the numbers of testees}} \end{align*}
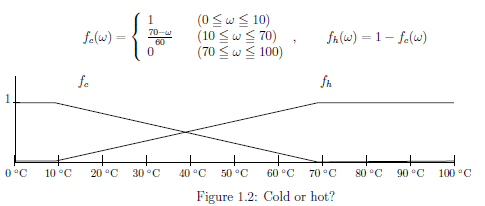
Therefore, for example,

$(A_1)$:

You choose one person from the testees, and you ask him/her whether the water (with 55℃) is "cold" or "hot" ?. Then the probability that he/she says$ \left[\begin{array}{ll} {} \mbox{"cold"} \\ {} \mbox{"hot"} \end{array}\right] $ is given by $ \left[\begin{array}{ll} {}f_{\text c}(55)=0.25 \\ {} f_{\text h}(55)=0.75 \end{array}\right] $

In what follows, let us describe the statement $(A_1)$ in terms of quantum language (i.e., Axiom 1). Define the state space $\Omega$ such that $$ \mbox{$\Omega=$ interval $[0, 100](\subset {\mathbb R}$(= the set of all real numbers))} $$

and measured value space $X=\{c, h\}$ ( where "$c$" and "$h$" respectively means "cold" and "hot").
Here, consider the "[C-H]-thermometer" such that

$(A_2)$:

for water with $\left.\begin{array}{ll}\omega \\ {}\end{array}\right.$℃ , [C-H]-thermometer presents$ \left[\begin{array}{ll} {} \mbox{c} \\ {} \mbox{h} \end{array}\right] $with probability$ \left[\begin{array}{ll} {} f_{\text c}(\omega) \\ {} f_{\text h}(\omega) \end{array}\right] $. This [C-H]-thermometer is denoted by ${\mathsf O} =$ $(f_{c},f_{h})$

Note that this [C-H]-thermometer can be easily realized by "random number generator". Here, we have the following identification:

$(A_3)$:

$\qquad$(A$_1$)$\Longleftrightarrow$(A$_2$)

Therefore, the statement $(A_1)$ in ordinary language can be interpreted in terms of measurement theory as follows.

$(A_4)$:

When an observer takes a measurement by [C-H]-insrument(= measuring instrument ${\mathsf O} =(f_{\text c},f_{\text h})$) for water (= System (measuring object)) with 55℃ (state $(=\omega =55 \in \Omega) )$, the probability that measured value $ \left[\begin{array}{ll} \mbox{c} \\ \mbox{h} \end{array}\right]$ is obtained is given by $\left[\begin{array}{ll} f_{\mbox{c}}(55)=0.25 \\ f_{\mbox{h}}(55)=0.75 \end{array}\right]$

That is, we get the following translation $$ (A_1) \xrightarrow[\mbox{translation}]{}　(A_4) $$ You may think that

This is only translation, and so, there is no development.
However, our purpose in this book is

to show the great power of description of quantum language
The above example will be again discussed in the following chapter(Example 2.31).