Measurement theory (= quantum language ) is formulated as follows. \[ \underset{\mbox{ (=quantum language)}}{\fbox{pure measurement theory (A)}} := \underbrace{ \underset{\mbox{ (\(\S\)2.7)}}{ \overset{ [\mbox{ (pure) Axiom 1}] }{\fbox{pure measurement}} } + \underset{\mbox{ ( \(\S \)10.3)}}{ \overset{ [{\mbox{ Axiom 2}}] }{\fbox{Causality}} } }_{\mbox{ a kind of incantation (a priori judgment)}} + \underbrace{ \underset{\mbox{ (\(\S\)3.1) }} { \overset{ {}}{\fbox{Linguistic interpretation}} } }_{\mbox{ the manual on how to use spells}} \] Now we can explain Axiom 1 (measurement).

2.7.1 Axiom1(measurement)

With any system $S$, a basic structure $[ {\mathcal A} \subseteq \overline{\mathcal A} \subseteq {B(H)}]$ can be associated in which measurement theory of that system can be formulated. A state (or precisely, { pure state}) of the system$S$ is represented by an element of state space ${\frak S}^p({\mathcal A}^*)$. An observable n(= measuring insrument ) is represented by a $C^*$-obvervable ${\mathsf O}$ ${{=}}$ $(X , {\cal F} , F{})$ in ${\mathcal A}$ ( or, $W^*$-obvervable ${\mathsf O}$ ${{=}}$ $(X , {\cal F} , F{})$ in $\overline{\mathcal A}$ ).

$(A_1):$ An observer takes a measurement of an observable [${\mathsf O}$] for a state $\rho$, and gets a measured value $x (\in X )$.

In a basic structure $[ {\mathcal A} \subseteq \overline{\mathcal A} \subseteq {B(H)}]$, consider a $W^*$-measurement ${\mathsf M}_{\overline{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F{}), S_{[{}\rho] } \big)$ $\Big($ or, $C^*$-measurement ${\mathsf M}_{{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F{}), S_{[{}\rho] } \big)$ $\Big)$.

Preparation2.30 That is, consider
$\bullet$ a $W^*$-measurement ${\mathsf M}_{\overline{\mathcal A}} \bigl({\mathsf O} , S_{[{}\rho{}] } \bigl)$ $\Big($ or, $C^*$-measurement ${\mathsf M}_{{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F{}), S_{[{}\rho] } \big)$ $\Big)$ of an observable ${\mathsf O}{{=}} (X, {\cal F} , F{})$ for a state $\rho(\in {\frak S}^p({\cal A}^*))$
Note that
$(A_2):$ $\left\{\begin{array}{ll} \mbox{ $W^*$-measurement ${\mathsf M}_{\overline{\mathcal A}} \big({\mathsf O} , S_{[\rho]} \big)$} &\cdots \mbox{ ${\mathsf O}$ is $W^*$- observable ,$\rho \in {\frak S}^p ({\mathcal A}^* )$ } \\ \mbox{ $C^*$-measurement ${\mathsf M}_{{\mathcal A}} \big({\mathsf O} , S_{[\rho]} \big)$} &\cdots \mbox{ ${\mathsf O}$ is $C^*$- observable ,$\rho \in {\frak S}^p ({\mathcal A}^* )$ } \end{array}\right. $
In this lecture, we mainly devote ourselves to $W^*$-measurements.
The following axiom is a kind of generalization (or, a linguistic turn) of Born's probabilistic interpretation of quantum mechanics. That is, \begin{align} \overset{\mbox{ (the law proposed by Born)}}{ \underset{\mbox{ (physics)}}{ {\fbox{quantum mechanics (Born's quantum measurement)}} } } \xrightarrow[\mbox{ linguistic turn}]{} \overset{\mbox{ (a kind of spell)}}{ \underset{\mbox{ (metaphysics, language)}}{ {\fbox{measurement theory(Axiom 1)}} } } \end{align}
The linguistic turn expands coverage very much：For example,



$ \underset{\mbox{(Japanese proverb)}}{\fbox{ even monkeys fall from trees}} $





$\Large{\mbox{Monkey changes to }} \left\{\begin{array}{ll} \Large{\mbox{Homer}} \\ \small{\mbox{(Homer sometimes nods)}} \\ \\ \Large{\mbox{horse}} \\ \small{\mbox{( It is a good horse that never stumbles.)}} \\ \\ \cdots \end{array}\right\} \mbox{} $

Axiom 1(measurement) pure type${\mathsf M}_{\overline{\mathcal A}} \big({\mathsf O}{{}}, S_{[{}\rho] }\big)$
( This can be read under the preparation to this section)
With any system $S$, a basic structure $[ {\mathcal A} \subseteq \overline{\mathcal A}]_{B(H)}$ can be associated in which measurement theory of that system can be formulated. In $[ {\mathcal A} \subseteq \overline{\mathcal A}]_{B(H)}$, consider a $W^*$-measurement ${\mathsf M}_{\overline{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F{}), S_{[{}\rho] } \big)$ $\Big($ or, $C^*$-measurement ${\mathsf M}_{{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F{}), S_{[{}\rho] } \big)$ $\Big)$. That is, consider
$\bullet$$\;\;$ a $W^*$-measurement ${\mathsf M}_{\overline{\mathcal A}} \bigl({\mathsf O} , S_{[{}\rho{}] } \bigl)$ $\Big($ or, $C^*$-measurement ${\mathsf M}_{{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F{}), S_{[{}\rho] } \big)$ $\Big)$ of an observable ${\mathsf O}{{=}} (X, {\cal F} , F{})$ for a state $\rho(\in {\frak S}^p({\cal A}^*):\mbox{state})$

Then, the probability that a measured value $x$ $( \in X )$ obtained by the $W^*$-measurement ${\mathsf M}_{\overline{\mathcal A}} \bigl({\mathsf O} , S_{[{}\rho{}] } \bigl)$ $\Big($ or, {$C^*$-measurement} ${\mathsf M}_{{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F{}), S_{[{}\rho] } \big)$ $\Big)$ belongs to $ \Xi $ $(\in {\cal F}{})$ is given by \begin{align*} \rho( F(\Xi)) (\equiv {}_{{{\mathcal A}^*}}(\rho, F(\Xi) )_{\overline{\mathcal A}} ) \end{align*} (if $F(\Xi)$ is essentially continuous at $\rho$, or see (2.56) in Definition 2.19 ).
$\fbox{Note 2.4}$[The Bohr?Einstein debates]. The above axiom is due to Max Born (1926). There are many opinions for the term "probability". For example, Einstein sent Born the following letter (1926):
($\sharp$): Quantum mechanics is certainly imposing. But an inner voice tells me that it is not yet the real thing. The theory says a lot, but does not really bring us any closer to the secret of the "old one." I, at any rate, am convinced that He does not throw dice.
That is, Einstein's words $(\sharp)$ means that
The concept of "probability" is metaphysical
In this sense that \begin{align*} \overset{\mbox{ }}{ \underset{\mbox{(Einstein)}}{\fbox{$\mbox{Realistic world view}$}}} \quad \underset{\mbox{v.s.}}{\longleftrightarrow} \quad \overset{\mbox{}}{ \underset{\mbox{(Bohr, Born)}}{\fbox{$\mbox{Linguistic world view}$}}} \end{align*} I want to believe that both Born and Einstein are right. That is because I assert that quantum mechanics is not physics. Namely, quantum mechanics is physics only in the case of ⑤ of Fig 1.1 in $\S$1.1,1.
2.7.2 A simplest example

Now we shall describe Example1.2 ( Cold or hot?) in terms of quantum language (i.e.,Axiom 1).

Example 2.31[(continued from Example1.2) The measurement of "cold or hot" for water in a cup ]

Consider the classical basic structure: \begin{align*} \mbox{ $[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]$ } \end{align*}

Here, $\Omega=$ the closed interval $[0,100](\subset {\mathbb R})$ with Lebesgue measure $\nu$. The state space ${\frak S}^p(C_0(\Omega)^*)$ is characterized as

\begin{align*} {\frak S}^p(C_0(\Omega)^*)=\{ \delta_\omega \in {\mathcal M}(\Omega) \;|\; \omega \in \Omega \} \approx \Omega =[0,100] \end{align*}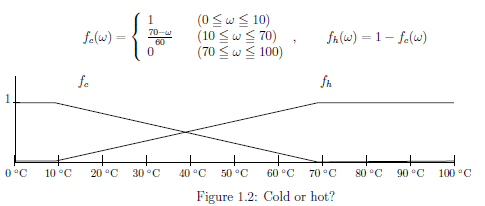

In Example 1.2, we consider this [C-H]-thermometer ${\mathsf O} =$ $(f_{{c}},f_{{h}})$, where the state space $\Omega=[0,100]$, the measured value space $X=\{ {c,h}\}$. That is,

$(\sharp)$:$ \qquad \qquad f_{c} (\omega) = \left\{\begin{array}{ll} 1 & \quad (0 {{\; \leqq \;}}\omega {{\; \leqq \;}}10 ) \\ \frac{70- \omega}{60} & \quad (10 {{\; \leqq \;}}\omega {{\; \leqq \;}}70 ) \\ 0 & \quad (70 {{\; \leqq \;}}\omega {{\; \leqq \;}}100 ) \end{array}\right., \qquad f_{h} (\omega) = 1- f_{c} (\omega) $

Then, we have the (cold-hot) observable ${\mathsf O}_{ch}= (X , 2^X, F_{ch} )$ in $L^\infty ( \Omega )$ such that

\begin{align*} & [F_{ch}(\emptyset )](\omega ) = 0, \quad &{}& [F_{ch}(X )](\omega ) = 1 \\ & [F_{ch}(\{c\})](\omega ) = f_{c} (\omega ), &{}& [F_{ch}(\{h\})](\omega ) = f_{h} (\omega ) \end{align*}

Thus, we get a measurement ${\mathsf M}_{L^\infty ( \Omega )} ( {\mathsf O}_{ch}, S_{[\delta_\omega]} )$ $($ or in short, ${\mathsf M}_{L^\infty ( \Omega )} ( {\mathsf O}_{ch}, S_{[{\omega}]} )$. Therefore, for example, putting $\omega=55$°C, we can, by Axiom 1 ($\S$2.7), represent the statement (A$_1$) in Example 1.2 as follows.

(a): the probability that a measured value$x(\in X {{=}} \{c, h\})$ obtained by measurement $\left.\begin{array}{ll}{\mathsf M}_{L^\infty ( \Omega )} ( {\mathsf O}_{ch}, S_{[ \omega(=55)]} ) \end{array}\right.$ belongs to set $ \left[\begin{array}{ll} {} \emptyset \\ \{ \mbox{c}\} \\ \{ {h} \} \\ \{ {c} ,{h}\} \end{array}\right] $ is given by $ \left[\begin{array}{ll} {} [F_{ch}( \emptyset )](55)= 0 \\ {} [F_{ch}( \{ { c} \} )](55)= 0.25 \\ {} [F_{ch}( \{ { h} \} )](55)= 0.75 \\ {} [F_{ch}( \{ { c} , { h} \} )](55)= 1 \end{array}\right] $