2.10.1: de Broglie paradox in $B({\mathbb C}^2)$
Axiom1 (measurement in $\S$2.7) includes the paradox ( that is, so called de Broglie paradox :"there is something faster than light"). In what follows, we shall explain de Broglie paradox in $B({\mathbb C}^2)$, though the original idea is mentioned in $B(L^2({\mathbb R}))$ (cf. $\S$11.2). Also, it should be noted that the argument below is essentially the same as
the Stern=Gerlach experiment.
Example 2.37 [de Broglie paradox in $B({\mathbb C}^2)$ ]
Let $H$ be a two dimensional Hilbert space, i.e., $H={\mathbb C}^2$. Consider the quantum basic structure:
\begin{align*}
[B({\mathbb C}^2)\subseteq B({\mathbb C}^2 ) \subseteq {B({\mathbb C}^2 )}]
\end{align*}
Now consider the situation in the following Figure 2.11.
Let us explain this figure in what follows. Let $f_1, f_2 \in H$ such that
\begin{align*}
f_1
=
\left[\begin{array}{l}
1
\\
0
\end{array}\right]
\in {\mathbb C}^2 ,
\qquad
f_2
=
\left[\begin{array}{l}
0
\\
1
\end{array}\right]
\in {\mathbb C}^2
\end{align*}
Put
\begin{align*}
u=\frac{f_1 +f_2}{{\sqrt 2}}
\end{align*}
Thus, we have the state $\rho = |u \rangle \langle u |$ $(\in {\frak S}^p(B({\mathbb C}^2)))$. Let $U (\in B({\mathbb C}^2 ))$ be an unitary operator such that
\begin{align*}
U
=
\left[\begin{array}{ll}
1 & 0 \\
0 & e^{i\pi/2 }
\end{array}\right]
\quad
\end{align*}
and let $\Phi: B({\mathbb C}^2) \to B({\mathbb C}^2) $ be the homomorphism such that
\begin{align*}
\Phi(F) = U^* F U
\qquad
(\forall F \in B({\mathbb C}^2)
)
\end{align*}
Consider the observable ${\mathsf O}_f=(\{1,2\}, 2^{\{1,2\}}, F)$ in $B({\mathbb C}^2 )$ such that
\begin{align*}
&
F(\{1\}) = |f_1 \rangle \langle f_1 | ,
\quad F(\{ 2 \}) = |f_2 \rangle \langle f_2 |
\end{align*}
and thus, define the observable $\Phi {\mathsf O}_f=(\{1,2\}, 2^{\{1,2\}}, \Phi F)$ by
\begin{align*}
\Phi F (\Xi)
=
U^* F(\Xi ) U
\qquad
(\forall \Xi \subseteq \{1, 2\} )
\end{align*}
Let us explain Figure 2.38. The photon P with the state $u=\frac{1}{\sqrt{2}}( f_1+f_2 )$ ( precisely, $|u \rangle \langle u |$ ) rushed into the half-mirror 1
| $(A_1):$ | the $f_1$ part in $u$ passes through half-mirror 1, and goes along course 1 to photon detector $D_1$.
|
| $(A_2):$ | the $f_2$ part in $u$ rebounds on half-mirror 1 (and strictly saying, the $f_2$ changes to ${\sqrt{-1}}f_2$, we are not concerned with it ), and goes along course 2 to photon detector $D_2$.
|
Thus, we have the measurement:
\begin{align}
{\mathsf M}_{B({\mathbb C}^2)} ( \Phi{\mathsf O}_f, S_{[\rho]} )
\tag{2.77}
\end{align}
And thus, we see:
| $(B):$ | The probability that a $\left[\begin{array} \mbox{\rm measured\;\; value }1 \\ \mbox{measured value }2 \end{array}\right]$ is obtained by the measurement $
{\mathsf M}_{B({\mathbb C}^2)} ( \Phi{\mathsf O}_f, S_{[\rho]} )
$ is given by
\begin{align*}
\left[\begin{array}{l}
\mbox{Tr}(\rho \cdot \Phi F(\{1\}) )
\\
\mbox{Tr}(\rho \cdot \Phi F(\{2\}) )
\end{array}\right]
=
\left[\begin{array}{l}
\langle u, \Phi F(\{1\})u \rangle
\\
\langle u, \Phi F(\{2\}) u \rangle
\end{array}\right]
=
\left[\begin{array}{l}
\langle Uu, F(\{1\}) Uu \rangle
\\
\langle Uu, F(\{2\}) U u \rangle
\end{array}\right]
=
\left[\begin{array}{l}
| \langle u, f_1 \rangle|^2
\\
| \langle u, f_2 \rangle|^2
\end{array}\right]
=
\left[\begin{array}{l}
\frac{1}{2}
\\
\frac{1}{2}
\end{array}\right]
\end{align*}
|
This is easy, but it is deep in the following sense.
| $(C):$ | Assume that
Detector $D_1$ and Detector $D_2$ are very far apart.
And assume that photon P is discovered at detector $D_1$. Then, we are troubled if photon P is also discovered at detector $D_2$. Thus, in order to avoid this difficulty, photon P (discovered at detector $D_1$) has to eliminate the wave function $\frac{\sqrt{-1}}{\sqrt{2}}f_2$ in an instant. In this sense, the (B) implies that
\begin{align*}
\mbox{
there may be something faster than light
}
\end{align*}
|
 |
|
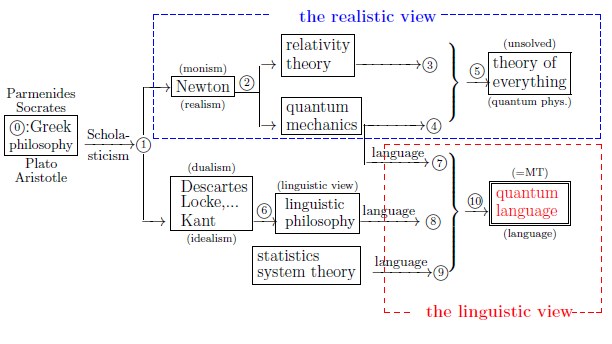
$\qquad \qquad $Fig. 1.1; history of world-descriptions |
This is the de Broglie paradox.
From the view point of quantum language, we give up to solve the paradox, that is, we ( as well as Mermin ) declare
Stop being bothered!
Or
If you want to be bothered,
be bothered in physics ⑤ in Figure 1.1 ( in $\S$1.1) !
| $\fbox{Note 2.8}$ | The de Broglie paradox (i.e., there may be something faster than light ) always appears in quantum mechanics. For example, the readers should confirm that it appears in Example 2.36 (Schtern-Gerlach experiment). I think that
| $\bullet$ | the de Broglie paradox is the only paradox in quantum mechanics
|
The readers will find that the other paradoxes ( see "paradox" in the index of this book ) in quantum mechanics are solved in this book.
|
