Consider the two dimensional Hilbert space $H= {\mathbb C}^2$, And therefore, we get the non-commutative basic algebra $ B(H)$, that is, nthe algebra composed of all $2 \times 2$ matrices. Thus, we have the quantum basic structure:
since the dimension of $H$ is finite.
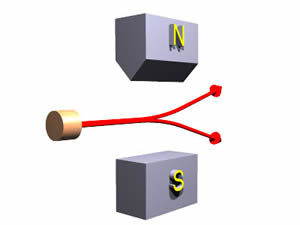
Example2.36 Assume that we examine the beam (of silver particles (or simply, electrons) after passing through the magnetic field. Then, as seen in the following figure, we see that all particles are deflected either equally upwards or equally downwards in a 50:50 ratio. See Figure 2.10.
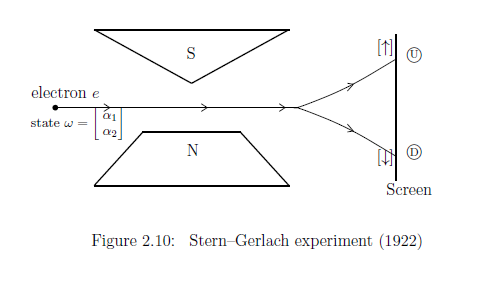
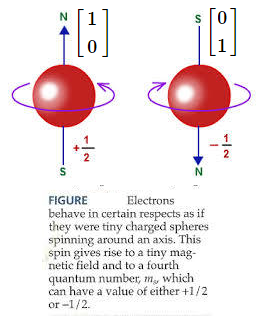
The spin state of an electron $P$ is represented by $\rho (= |\omega \rangle \langle \omega |)$, where $\omega \in {\mathbb C}^2 $ such that $\| \omega \|=1$. Put $ \omega = \left[\begin{array} \; \alpha_1 \\ \; \alpha_2 \end{array}\right] $ where, $||\omega ||^2 = |\alpha_1|^2 +|\alpha_2|^2 =1$). Define ${\mathsf O}_z$ $\equiv$ $({}Z , 2^Z , F_z {})$, the spin observable concerning the $z$-axis, such that, $Z= \{ \uparrow , \downarrow \}$ and
\begin{align} F_z ({}\{ \uparrow \}{}) = \left[\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right] , \quad F_z ({}\{ \downarrow \}{}) = \left[\begin{array}{ll} 0 & 0 \\ 0 & 1 \end{array}\right] , \quad F_z ({}\emptyset{}) = \left[\begin{array}{ll} 0 & 0 \\ 0 & 0 \end{array}\right] , \quad F_z ({}\{ \uparrow ,\downarrow \}{}) = \left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right] . \end{align} Here, Born's quantum measurement theory (the probabilistic interpretation of quantum mechanics) says that| $(\sharp):$ | When a quantum measurement ${\mathsf M}_{B({\mathbb C}^2)}({\mathsf O}, S_{[\rho]})$ is taken, the probability that \begin{align*} \mbox{} \mbox{ a measured value } \left[\begin{array}{ll} \mbox{$\uparrow$} \\ \mbox{$\downarrow$} \end{array}\right] \mbox{is obtained } \mbox{is given by} \left[\begin{array}{ll} \langle \omega, F^z(\{ \uparrow\}) \omega \rangle =|\alpha_1|^2 \\ \\ \langle \omega, F^z(\{ \downarrow\}) \omega \rangle = |\alpha_2|^2 \end{array}\right] \end{align*} |
That is, putting $\omega$ $(= \left[\begin{array}{l} \; \alpha_1 \\ \; \alpha_2 \end{array}\right] )$, we says that
| $(\flat)$ | \begin{align*} & \mbox{When the electron with a spin state state $\rho$ progresses in a magnetic field}, \\ & \mbox{the probability that the Geiger counter } \left[\begin{array}{ll} \mbox{(Uper)} \\ \mbox{(Down)} \end{array}\right] \mbox{ sounds} \\ & \mbox{is give by} \left[\begin{array}{ll} \big[ \overline{\alpha}_1 \;\;\; \overline{\alpha}_2 \big] \left[\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right] \left[\begin{array} \; \alpha_1 \\ \; \alpha_2 \end{array}\right] =|\alpha_1|^2 \\ \\ \big[ \overline{\alpha}_1 \;\;\; \overline{\alpha}_2 \big] \left[\begin{array}{ll} 0 & 0 \\ 0 & 1 \end{array}\right] \left[\begin{array} \; \alpha_1 \\ \; \alpha_2 \end{array}\right] =|\alpha_2|^2 \end{array}\right]\mbox{} \end{align*} |
We can define ${\mathsf O}^x$ $\equiv$ $({}X , 2^X , F^x {})$, the spin observable concerning the $x$-axis, such that, $X= \{ \uparrow _{x} , \downarrow _{x} \}$ and
\begin{align} F^x ({}\{ \uparrow _{x} \}{}) = \left[\begin{array}{ll} 1/2 & 1/2 \\ 1/2 & 1/2 \end{array}\right] , \quad F^x ({}\{ \downarrow _{x} \}{}) = \left[\begin{array}{ll} 1/2 & -1/2 \\ -1/2 & 1/2 \end{array}\right] . \tag{2.74} \end{align}And furthermore, we can define ${\mathsf O}^y$ $\equiv$ $({}Y , 2^Y , F^y {})$, the spin observable concerning the $y$-axis, such that, $Y= \{ \uparrow _{y} , \downarrow _{y} \}$ and
\begin{align} F^y ({}\{ \uparrow _{y} \}{}) = \left[\begin{array}{ll} 1/2 & i/2 \\ -i/2 & 1/2 \end{array}\right] , \quad F^y ({}\{ \downarrow _{y} \}{}) = \left[\begin{array}{ll} 1/2 & -i/2 \\ i/2 & 1/2 \end{array}\right] , \tag{2.75} \end{align} where $i= \sqrt{-1}$. Here, putting \begin{align*} {\hat S}_x = F_x(\{\uparrow \}) - F_x(\{\downarrow \}), \quad {\hat S}_y = F_y(\{\uparrow \}) - F_y(\{\downarrow \}) , \quad {\hat S}_z = F_z(\{\uparrow \}) - F_z(\{\downarrow \}) \end{align*} we have the following commutation relation: \begin{align} {\hat S}_y {\hat S}_z- {\hat S}_z {\hat S}_y =2i {\hat S}_x, \quad {\hat S}_z {\hat S}_x- {\hat S}_x {\hat S}_z =2i {\hat S}_y, \quad {\hat S}_x {\hat S}_y- {\hat S}_y {\hat S}_x =2i {\hat S}_z \tag{2.76} \end{align}Supplement
The above (2.76) may be too beautiful. That is, some may feel that
and quantum mechanics follows.
