5.2.1: Inference problem ( Statistical inference )
Before we mention Fisher's maximum likelihood method, we exercise the following problem:
Problem 5.2[Urn problem( =Example 2.34),A simplest example of Fisher's maximum likelihood method]
There are two urns $U_1$ and $U_2$. The urn $U_1$ [resp. $U_2$] contains $8$ white and $2$ black balls [resp. $4$ white and $6$ black balls].
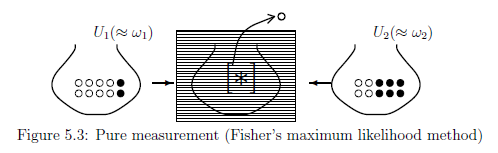
Here consider the following procedures(i) and (ii).
| $(i):$ | One of the two (i.e., $U_1$ or $U_2$) is chosen and is settled behind a curtain. Note, for completeness, that you do not know whether it is $U_1$ or $U_2$.
|
| (ii): | Pick up a ball out of the unknown urn behind the curtain. And you find that the ball is white.
|
Here, we have the following problem:
| ${\rm (iii)}:$ | Infer the urn behind the curtain, $U_1$ or $U_2$?
|
The answer is easy, that is, the urn behind the curtain is $U_1$. That is because the urn $U_1$ has more white balls than $U_2$. The above problem is too easy, but it includes the essence of Fisher maximum likelihood method.
5.2.2: Fisher's maximum likelihood method in measurement theory
We begin with the following notation:
Notation 5.3 [${\mathsf M}_{\overline{\mathcal A}} ({\mathsf O}, S_{[*]})$]
Consider the measurement ${\mathsf M}_{\overline{\mathcal A}} $ $({\mathsf O} {{=}} (X, {\cal F}, F),$ $ S_{[\rho]})$ formulated in the basic structure $[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$. Here, note that
| $(A_1):$ | In most cases that the measurement ${\mathsf M}_{\overline{\mathcal A}} $ $({\mathsf O} {{=}} (X, {\cal F}, F),$ $ S_{[\rho]})$ is taken, it is usual to think that the state $\rho \;(\in {\frak S}^p ({\cal A}^*))$ is unknown.
|
That is because
| $(A_2):$ | the measurement ${\mathsf M}_{\cal A} ({\mathsf O}, S_{[\rho]})$ may be taken in order to know the state $\rho$.
|
Therefore, when we want to stress that
\begin{align}
\mbox{
we do not know the state
$\rho$
}
\end{align}
The measurement ${\mathsf M}_{\overline{\mathcal A}} $ $({\mathsf O} {{=}} (X, {\cal F}, F),$ $ S_{[\rho]})$ is often denoted by
| $(A_3):$ | ${\mathsf M}_{\overline{\mathcal A}} $ $({\mathsf O} {{=}} (X, {\cal F}, F),$ $ S_{[\ast]})$
|
Furthermore, consider the subset $K (\subseteq {\frak S}^p({\mathcal A}^*) )$. When we know that the state $\rho$ belongs to $K$, ${\mathsf M}_{\overline{\mathcal A}} $ $({\mathsf O} {{=}} (X, {\cal F}, F),$ $ S_{[\ast]})$ is denoted by ${\mathsf M}_{\overline{\mathcal A}} ({\mathsf O}, S_{[*]}(\!(K)\!))$. Therefore, it suffices to consider that
\begin{align}
{\mathsf M}_{\overline{\mathcal A}} ({\mathsf O}, S_{[\ast]})
=
{\mathsf M}_{\overline{\mathcal A}} ({\mathsf O}, S_{[\ast]}(\!({\frak S}^p({\mathcal A}^*) )\!) )
\end{align}
Using this notation ${\mathsf M}_{\overline{\mathcal A}} ({\mathsf O}, S_{[*]})$, we characterize our problem (i.e., inference) as follows.
Problem 5.4 [Inference problem]
| $(a):$ | Assume that a measured value obtained by ${\mathsf M}_{\overline{\mathcal A}}({\mathsf O} {{=}} (X, {\cal F}, F), S_{[*]}(\!(K)\!) )$ belongs to $\Xi (\in {\cal F})$. Then, infer the unknown state $[*] \;(\in \Omega)$
|
or,
| $(b):$ | Assume that a measured value $(x,y)$ obtained by ${\mathsf M}_{\overline{\mathcal A}}({\mathsf O} {{=}} (X \times Y, {\cal F} \boxtimes {\cal G}, H), S_{[*]}(\!(K)\!) )$ belongs to $\Xi \times Y$ $(\Xi \in {\cal F})$. Then, infer the probability that $y \in \Gamma $.
|
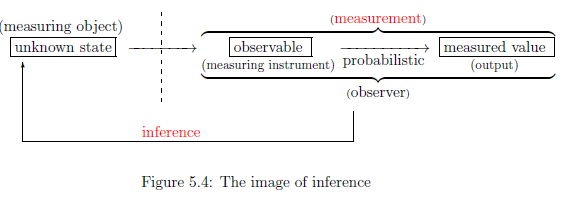
Before we answer the problem, we emphasize the reverse relation between "inference" and "measurement".
The measurement is "the view from the front", that is,
| $(B1):$ | $
\qquad
\qquad
(\mbox{observable} [{\mathsf O}], {\mbox{{state}}}[\omega(\in \Omega)])
\xrightarrow[{\mathsf M}_{L^\infty (\Omega)}({\mathsf O},
S_{[\omega]})]{
\quad {{\mbox{ measurement}}} \quad}
\mbox{measured value} {[x (\in X)]}
$
|
On the other hand, the inference is "the view from the back", that is,
| $(B2):$ | $
\qquad
\qquad
(\mbox{observable} [{\mathsf O}], \mbox{measured value} [x \in \Xi ( \in {\cal F})])
\xrightarrow[{\mathsf M}_{L^\infty (\Omega)}({\mathsf O},
S_{[\ast]})]{
\quad {\mbox{ inference}}\quad}
{\mbox{ state }}{[\omega (\in \Omega)]}
$
|
In this sense, we say that
the inference problem is the reverse problem of measurement
Therefore, it suffices to image Fig. 5.4.
In order to answer the above problem 5.4Problem, we shall describe Fisher maximum likelihood method in terms of measurement theory.
Theorem 5.5 [(Answer to Problem 5.4 (b)): Fisher's maximum likelihood method(the general case)]
Consider the basic structure
\begin{align}
[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]
\end{align}
Assume that a measured value$(x,y)$ obtained by a measurement ${\mathsf M}_{\overline{\mathcal A}}({\mathsf O} {{=}} (X \times Y, {\cal F} \boxtimes {\cal G}, H), S_{[*]}(\!(K)\!) )$ belongs to $\Xi \times Y$ $(\Xi \in {\cal F})$. Then, there is reason to infer that the probability $P(\Gamma)$ that $y \in \Gamma $ is equal to
\begin{align}
P(\Gamma)
=
\frac{\rho_0( H(\Xi \times \Gamma ))}{\rho_0( H(\Xi \times Y ))}
\quad( \forall \Gamma \in {\mathcal G} )
\end{align}
where, $\rho_0 \in K$ is determined by.
\begin{align}
\rho_0 ( H(\Xi \times Y ) ) = \max_{\rho \in K} \rho ( H(\Xi \times Y ) )
\tag{5.7}
\end{align}
Proof. Assume that $\rho_1, \rho_2 \in K$ and $\rho_1(H(\Xi \times Y)) <\rho_2(H(\Xi \times Y)) $. By Axiom 1 ( measurement: $\S$2.7)
| $(i):$ | the probability that {a measured value}$(x,y)$ obtained by a measurement ${\mathsf M}_{\overline{\mathcal A}} ({\mathsf O}, S_{[\rho_1]})$ belongs to $\Xi \times Y$ is equal to $\rho_1(H(\Xi \times Y)) $
|
| $(ii)$: | the probability that {a measured value}$(x,y)$ obtained by a measurement ${\mathsf M}_{\overline{\mathcal A}} ({\mathsf O}, S_{[\rho_2]})$ belongs to $\Xi \times Y$
is equal to $\rho_2(H(\Xi \times Y)) $
|
Since we assume that $\rho_1(H(\Xi \times Y)) <\rho_2(H(\Xi \times Y)) $, we can conclude that "(i) is more rare than (ii)". Thus, there is a reason to infer that $[*]=\omega_2$. Therefore, the $\rho_0$ in (5.7) is reasonable. Since the probability that a measured value$(x,y)$ obtained by ${\mathsf M}_{\overline{\mathcal A}} ({\mathsf O}, S_{[\rho_0]} )$ belongs to $\Xi \times \Gamma $ is given by $\rho_0 (
H(
\Xi \times \Gamma
)
)
$, we complete the proof of Theorem 5.5.
QED
Theorem 5.6 [(Answer to Problem5.4(a)): {}Fisher's maximum likelihood method in classical case]
(i): Consider a measurement ${\mathsf M}_{L^\infty (\Omega)}({\mathsf O} $ ${{=}} (X, {\cal F}, F),$ $ S_{[*]}(\!( K )\!))$.
Assume that we know that a measured value obtained by a measurement ${\mathsf M}_{L^\infty (\Omega)}({\mathsf O}, S_{[*]}(\!( K )\!))$ belongs to $\Xi \;(\in {\cal F})$. Then, there is a reason to infer that the unknown state {{state}} $[*]$
is $\omega_0 \;(\in \Omega)$ such that
\begin{align}
[F(\Xi)](\omega_0)
= \max_{\omega \in \Omega} [F(\Xi)](\omega)
\tag{5.8}
\end{align}
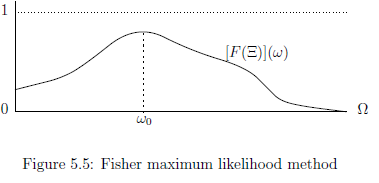
(ii): Assume that a measured value $x_0 \;(\in {X})$ is obtained by a measurement ${\mathsf M}_{{L^\infty (\Omega) }}({\mathsf O} $ ${{=}} (X, {\cal F}, F),$ $ S_{[*]} (\!( K )\!))$. Define the likelihood function $f(x,\omega)$ by
\begin{align}
f(x, \omega) = \inf_{\omega_1 \in K}\Big[ \lim_{\Xi \ni x, [F(\Xi)](\omega_1) \not= 0,
\Xi \to \{x\} } \frac{[F(\Xi)](\omega )}{[F(\Xi)](\omega_1 )}
\Big]
\tag{5.9}
\end{align}
Then, there is a reason to infer that $[\ast]=\omega_0 (\in K)$ such that $f(x_0,\omega_0)=1$.
Proof.Consider Theorem 5.5 in the case that
\begin{align}
[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]
=
{
[C_0(\Omega ) \subseteq L^\infty (\Omega ) \subseteq B(
L^2 (\Omega )
]
}
\end{align}
Thus, in the measurement ${\mathsf M}_{L^\infty(\Omega ) }({\mathsf O} {{=}} (X \times Y, {\cal F} \boxtimes {\cal G}, H), S_{[*]}(\!(K)\!) )$, consider the case that
\begin{align}
&
\mbox{Fixed ${\mathsf O}_1 {{=}} (X , {\cal F}, F ), \;\;$
any ${\mathsf O}_2 {{=}} (Y, {\cal G}, G),$
}
\;\;
\\
&
{\mathsf O} {{=}}{\mathsf O}_1 \times {\mathsf O}_2
=(X \times Y, {\cal F} \boxtimes {\cal G}, F \times G),\;\;
\rho_0 = \delta_{\omega_0}
\end{align}
Then, we see
\begin{align}
P(\Gamma ) =
\frac{ [H(\Xi)](\omega_0) \times [G(\Gamma)](\omega_0)}{
[H(\Xi)](\omega_0) \times [G(Y)](\omega_0)}
=
[ G(\Gamma )](\omega_0)
\quad( \forall \Gamma \in {\mathcal G} )
\tag{5.10}
\end{align}
And, from the arbitrariness of ${\mathsf O}_2 $, there is a reason to infer that
\begin{align}
[*]=\delta_{\omega_0}( \approx \omega_0)\end{align}
QED
| $\fbox{Note 5.1}$ | The linguistic interpretation says that the state after measurement is non-sense. In this sense, the readers may consider that
| $(\sharp_1):$ | Theorem 5.6 is also non-sense
|
However, we say that
| $(\sharp_2):$ | in the sense of (5.10), Theorem 5.6 should be accepted.
|
or
| $(\sharp_3):$ | as far as classical system, it suffices to believe in Theorem 5.6
|
|
Answer 5.7 [The answer to Problem 5.2 by Fisher's maximum likelihood method]
Problem 5.2(written again)
You do not know which the urn behind the curtain is, $U_1$ or $U_2$.
Assume that you pick up a white ball from the urn.
The urn is $U_1$ or $U_2$? $\quad$ Which do you think?
The above will be answered as follows:
Consider the measurement ${\mathsf M}_{{L^\infty (\Omega) }} ({\mathsf O} {{=}}$ $
( \{ w,$ $ b \},$ $ 2^{\{ w, b \} } ,$ $ F)
,
S_{ [{}{\ast}]})$, where the observable ${\mathsf O}_{wb} = ( \{ w, b \}, 2^{\{ w, b \} } , F_{wb})$ in $L^\infty (\Omega)$ is defined by
\begin{align}
& [F_{wb}(\{ w \})](\omega_1)= 0.8, & \quad & [
F_{wb}(\{ b \})](\omega_1)= 0.2
\\
& [F_{wb}(\{ w \})](\omega_2)= 0.4, & \quad & [F_{wb}(\{ b \})]
(\omega_2)= 0.6
\tag{5.11}
\end{align}
Here, we see:
\begin{align}
&
\max \{[F_{wb}(\{w\})](\omega_1),
[F_{wb}(\{w\})](\omega_2)
\}
\\
=
&
\max \{0.8, 0.4\}
=
0.8
=
F_{wb}(\{w\})](\omega_1)
\end{align}
Then, Fisher's maximum likelihood method (Theorem 5.6) says that
\begin{align}
[\ast ] = \omega_1
\end{align}
Therefore, there is a reason to infer that the urn behind the curtain is $U_1$.
QED
| $\fbox{Note 5.2}$ | As seen in Figure 5.4, inference (Fisher maximum likelihood method) is the reverse of measurement (i.e., Axiom 1 due to Born). Here note that
| $(a):$ | Born's discovery "the probabilistic interpretation of quantum mechanics" in 1926
| | (b): | Fisher's great book "Statistical Methods for Research Workers" (1925)
|
Thus, it is surprising that Fisher and Born investigated the same thing in the different fields in the same age.
|
