6.4(1): Population variance (Confidence interval method)
6.4.1: Preparation (simultaneous normal measurement)
Consider the simultaneous normal measurement ${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$ $({\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$ $S_{[(\mu, \sigma)]})$ in $L^\infty({\mathbb R} \times {\mathbb R}_+)$. Here,recall that the simultaneous normal observable ${\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n} )$ is defined by
\begin{align}
&
[{{{G}}}^n
({\mathop{\mbox{$\times$}}}_{k=1}^n \Xi_k)]
(\omega)
=
{\mathop{\mbox{ $\times$}}}_{k=1}^n
[{{{G}}}(\Xi_k)](\omega)
\nonumber
\\
=
&
\frac{1}{({{\sqrt{2 \pi }\sigma{}}})^n}
\underset{{{\mathop{\mbox{$\times$}}}_{k=1}^n \Xi_k }}{\int \cdots \int}
\exp[{}- \frac{\sum_{k=1}^n ({}{x_k} - {}{\mu} )^2
}
{2 \sigma^2} {}] d {}{x_1} d {}{x_2}\cdots dx_n
\tag{6.45}
\\
&
\qquad
(\forall \Xi_k \in {\cal B}_{{\mathbb R}{}}^{}
(k=1,2,\ldots, n),
\quad
\forall {}{\omega}=(\mu, \sigma ) \in \Omega = {\mathbb R}\times {\mathbb R}_+).
\nonumber
\end{align}
where, note that
\begin{align}
&
\Omega = {\mathbb R} \times {\mathbb R}_+,
\qquad
X={\mathbb R}^n
\end{align}
The second state space $\Theta$ is
\begin{align}
&
\Theta = {\mathbb R}_+
\end{align}
Putting
\begin{align}
\overline{\mu}(x)
=
\frac{x_1 + x_2 + \cdots + x_n}{n}
\end{align}
we define the estimator $E: {\mathbb R}^n \to \Theta (\equiv {\mathbb R}_+ )$ by
\begin{align}
&
E(x)=E(x_1, x_2, \ldots , x_n )
=
\sqrt{
\frac{(x_1-\overline{\mu}(x))^2 + (x_2-\overline{\mu}(x))^2 + \cdots + (
x_n-\overline{\mu}(x))^2 }{n}
}
\end{align}
and the system quantity $\pi: \Omega \to \Theta $
by
\begin{align}
&
\Omega={\mathbb R} \times {\mathbb R}_+
\ni
\omega = (\mu, \sigma )
\mapsto \pi (\omega ) = \sigma \in \Theta={\mathbb R}_+
\end{align}
6.4.2: Confidence interval
Our present problem is as follows.
Problem 6.12 [Confidence interval for population variance]. Consider the simultaneous normal measurement ${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$ $({\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$ $S_{[(\mu, \sigma)]})$. Assume that a measured value$x \in X ={\mathbb R}^n$ is obtained by the measurement. Let $0 < \alpha \ll 1$.
Then, find the ${D}_{x}^{1- \alpha; \Theta}( \subseteq \Theta)$ (which may depend on $\mu$) such that
| $\bullet$ | the probability that $\sigma \in {D}_{x}^{1- \alpha; \Theta}$ is more than $1-\alpha$
|
Here, the more ${D}_{x}^{1- \alpha; \Theta}( \subseteq \Theta)$ is small, the more it is desirable.
Consider the following semi-distance $d_{\Theta}^{(1)}$ in $\Theta (={\mathbb R}_+ )$:
\begin{align}
d_{\Theta}^{(1)}(\theta_1, \theta_2)
=
|
\int_{\sigma_1}^{\sigma_2} \frac{1}{\sigma} d \sigma
|
=
|\log{\sigma_1} - \log{\sigma_2} |
\tag{6.46}
\end{align}
For any $ \omega=(\mu, {\sigma} ) (\in \Omega= {\mathbb R} \times {\mathbb R}_+ )$, define the positive number $\delta^{1- \alpha}_{\omega}$ $(> 0)$ such that:
\begin{align}
\delta^{1-\alpha}_{\omega}
&
=
\inf
\{
\eta > 0:
[F (E^{-1} (
{{ Ball}_{d_{\Theta}^{(1)}}}(\omega ; \eta))](\omega )
\ge 1- \alpha
\}
\nonumber
\\
&
=
\inf
\{
\eta > 0:
[F (E^{-1} (
{{ Ball}^C_{d_{\Theta}^{(1)}}}(\omega ; \eta))](\omega )
\le \alpha
\}
\tag{6.47}
\end{align}
where
\begin{align}
&
{{ Ball}^C_{d_{\Theta}^{(1)}}}(\omega ; \eta )
=
{{ Ball}^C_{d_{\Theta}^{(1)}}}((\mu ; {\sigma} ), \eta )
=
{\mathbb R} \times \{ \sigma' \;:\; |\log(\sigma'/{\sigma})| \ge \eta
\}
\\
=
&
{\mathbb R} \times \big(
(0,{\sigma} e^{-\eta}] \cup [{\sigma} e^{\eta} , \infty )
\big)
\tag{6.48}
\end{align}
Then,
\begin{align}
&
E^{-1}( {{ Ball}^C_{d_{\Theta}^{(1)}}}(\omega ; \eta ))
=
E^{-1}
\Big(
{\mathbb R} \times \big(
(0,{\sigma} e^{-\eta}] \cup [{\sigma} e^{\eta} , \infty )
\big)
\Big)
\nonumber
\\
=
&
\{
(x_1, \ldots , x_n )
\in
{\mathbb R}^n
\;:
\;
\Big(
\frac{\sum_{k=1}^n ( x_k -
\overline{\mu}
(x))^2}{n}
\Big)^{1/2}
\le
{\sigma} e^{ -\eta }
\mbox{ or }
{\sigma} e^{ \eta }
\le
\Big(
\frac{\sum_{k=1}^n ( x_k -
\overline{\mu}
(x))^2}{n}
\Big)^{1/2}
\}
\\
&
\tag{6.49}
\end{align}
Hence we see, by the Gauss integral (6.7), that
\begin{align}
&
[{{{G}}}^n
(E^{-1}({{ Ball}^C_{d_{\Theta}^{(1)}}}(\omega; \eta ))]
(\omega)
\nonumber
\\
=
&
\frac{1}{({{\sqrt{2 \pi }{\sigma}{}}})^n}
\underset{{
E^{-1}
\Big(
{\mathbb R} \times \big(
(0,{\sigma} e^{-\eta}] \cup [{\sigma} e^{\eta} , \infty )
\big)
\Big)
}}{\int \cdots \int}
\exp[{}- \frac{\sum_{k=1}^n ({}{x_k} - {}{\mu} )^2
}
{2 {\sigma}^2} {}] d {}{x_1} d {}{x_2}\cdots dx_n
\nonumber
\\
=
&
\int_0^{{n} e^{- 2 \eta}}
p^{\chi^2}_{n-1} (x )
dx
+
\int_{{n} e^{ 2 \eta}}^\infty
p^{\chi^2}_{n-1} (x )
dx
=
1-
\int_{{n} e^{- 2 \eta}}^{{n} e^{ 2 \eta}}
p^{\chi^2}_{n-1} (x )
dx
\tag{6.50}
\end{align}
Using the chi-squared distribution $p^{{\chi}^2}_{n-1}({ x} )$ (with $n-1$ degrees of freedom) in (6.8), define the $\delta^{1-\alpha}_{\omega}$ such that
\begin{align}
1-
\alpha
=
\int_{{n} e^{-2 \delta^{1-\alpha}_{\omega}}}^{{n} e^{2 \delta^{1-\alpha}_{\omega}}}
p^{\chi^2}_{n-1} (x ) dx
\tag{6.51}
\end{align}
where it should be noted that the $\delta^{1-\alpha}_{\omega}$ depends on only $\alpha$ and $n$. Thus, put
\begin{align}
\delta^{1-\alpha}_{\omega} = \delta^{1-\alpha}_{n}
\tag{6.52}
\end{align}
Hence we get, for any $x$ $(\in X)$, the $D_x^{{1 - \alpha, \Omega }}$ ( the $({1 - \alpha })$-confidence interval of $x$ ) as follows:
\begin{align}
D_x^{{1 - \alpha, \Omega }}
&
=
\{
{\omega}
(\in
\Omega)
:
d^{(1)}_\Theta (E(x),
\pi(\omega)
)
\le
\delta^{1 - \alpha}_{n}
\}
\nonumber
\\
&
=
\{ (\mu, \sigma ) \in {\mathbb R} \times {\mathbb R}_+
\;:
\;
\sigma e^{- \delta^{1 - \alpha }_{n} }
\le
\Big(
\frac{\sum_{k=1}^n ( x_k -
\overline{\mu}
(x))^2}{n}
\Big)^{1/2}
\le
\sigma e^{ \delta^{1 - \alpha }_{n} }
\}
\tag{6.53}
\end{align}
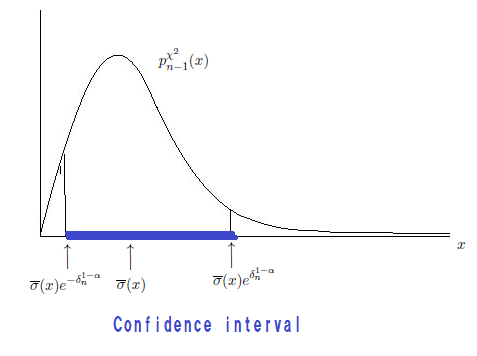
Recalling (6.4), i.e., $\overline{\sigma}(x) = \Big( \frac{\sum_{k=1}^n ( x_k - \overline{\mu} (x))^2}{n} \Big)^{1/2} ={(\frac{{\overline{SS}}(x)}{n})}^{1/2} $, we conclude that
\begin{align}
D_x^{{1 - \alpha, \Omega }}
&
=
\{ (\mu, \sigma ) \in {\mathbb R} \times {\mathbb R}_+
\;:
\;
\overline{\sigma}(x)
e^{ - \delta^{1 - \alpha }_{n}}
\le
\sigma
\le
\overline{\sigma}(x)
e^{ \delta^{1 - \alpha }_{n}}
\}
\nonumber
\\
&
=
\{ (\mu, \sigma ) \in {\mathbb R} \times {\mathbb R}_+
\;:
\;
\frac{e^{ - 2\delta^{1 - \alpha }_{n}}}{n}{\overline{SS}}(x)
\le
\sigma^2
\le
\frac{e^{ 2\delta^{1 - \alpha }_{n}}}{n}{\overline{SS}}(x)
\}
\tag{6.54}
\end{align}
And
\begin{align}
D_x^{{1 - \alpha, \Theta }}
&
=
\{ \sigma \in {\mathbb R}_+
\;:
\;
\overline{\sigma}(x)
e^{ - \delta^{1 - \alpha }_{n}}
\le
\sigma
\le
\overline{\sigma}(x)
e^{ \delta^{1 - \alpha }_{n}}
\}
\nonumber
\\
&
=
\{ (\mu, \sigma ) \in {\mathbb R} \times {\mathbb R}_+
\;:
\;
\frac{e^{ - 2\delta^{1 - \alpha }_{n}}}{n}{\overline{SS}}(x)
\le
\sigma^2
\le
\frac{e^{ 2\delta^{1 - \alpha }_{n}}}{n}{\overline{SS}}(x)
\}
\nonumber
\end{align}