8.3.1: Implication and contraposition

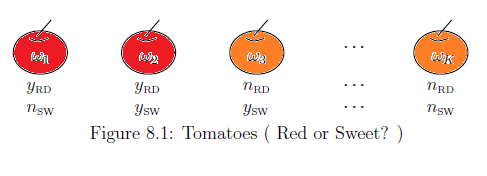
In Example 8.5, consider the case that $[{}F (\{( y_{{}_{RD}} , n_{{}_{SW}}) \}) {}] (\omega)=0$. In this case, we see \begin{align} \frac{ [{}F (\{(y_{{}_{RD}} , y_{{}_{SW}}) \}){}](\omega) } { [{}F (\{(y_{{}_{RD}} , y_{{}_{SW}}) \}){}](\omega) + [{}F (\{(y_{{}_{RD}} , n_{{}_{SW}}) \}){}](\omega) } =1 \end{align}

Therefore, when we know that a tomato $\omega $ is red, the probability, that the tomato $\omega $ is sweet, is equal to $1$. That is,

\begin{align} \mbox{" $[{}F (\{( y_{{}_{RD}} , n_{{}_{SW}}) \}) {}] (\omega) = 0$"} \quad \Longleftrightarrow \quad \Big[ \mbox{" Red"} \Longrightarrow \mbox{" Sweet"} \Big] \end{align}
Motivated by the above argument, we have the following definition.
Definition 8.6 [Implication] Consider the general basic structure \begin{align} [ {\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)] \end{align} Let ${\mathsf O}_{12}$ $=$ $(X_1 \times X_2 ,$ $ {\cal F}_1 \boxtimes {\cal F}_2 ,$ $ F_{12}{}{{=}} F_1 {\mathop{\overset{qp}{\times}}} F_2)$ be a quasi-product observable in ${{\overline{\mathcal A}}}$ Let $\rho \in {\frak S}^p({\mathcal A}^*) $, $\Xi_1$ $ \in {\cal F}_1 $, $\Xi_2$ $ \in {\cal F}_2$. Then, if it holds that \begin{align} \rho(F{}_{12}{} (\Xi_1 \times ( \Xi^c_2))) = 0 \end{align} this is denoted by \begin{align} [{\mathsf O}_{12}^{(1)};{\Xi_1}] \underset{ {\mathsf M}_{{\overline{\mathcal A}}} ({\mathsf O}_{12} , S_{ [\rho] }) }{ \Longrightarrow} [{\mathsf O}_{12}^{(2)};{\Xi_2}] \tag{8.5} \end{align}

Of course, this (8.5) should be read as follows.

$(A):$ Assume that a measured value $(x_1, x_2) (\in X_1 \times X_2)$ is obtained by a measurement ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{12} ,$ $ S_{ [\omega] })$. When we know that $x_1 \in \Xi_1$, then we can assure that $x_2 \in \Xi_2$.

The above argument is generalized as follows. Let ${\mathsf O}_{12...n}$ ${{=}}$ $(\times_{k=1}^n X_k ,$ $ \boxtimes_{k=1}^n{\cal F}_k , $ ${F}_{12...n} = \underset{k=1,2,...,n}{\mathop{\overset{qp}{\times}}} F_k )$ be a quasi-product observable in $\overline{\mathcal A}$. Let $\Xi_1$ $ \in {\cal F}_i $ and $\Xi_2$ $ \in {\cal F}_j$. Then, the condition

\begin{align} {}_{{\mathcal A}^*} \big(\rho, {F}^{(ij)}_{12...n} (\Xi_i \times ( \Xi^c_j)) \big) {}_{\overline{\mathcal A} } = 0 \end{align} (where, $\Xi^c=X \setminus \Xi$) is denoted by \begin{align} [{\mathsf O}_{12...n}^{(i)};{\Xi_i}] \underset{ {\mathsf M}_{{\overline{\mathcal A}}} ({\mathsf O}_{12...n} , S_{ [\rho] }) }{ \Longrightarrow} [{\mathsf O}_{12...n}^{(j)};{\Xi_j}] \tag{8.6} \end{align}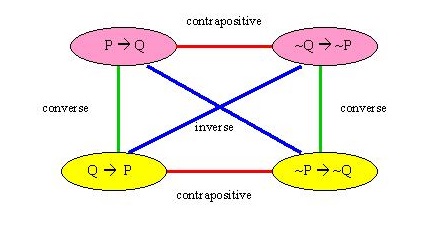

Theorem 8.7 [Contraposition] Let ${\mathsf O}_{12}$ $=$ $(X_1 \times X_2 ,$ $ {\cal F}_1 \times {\cal F}_2 ,$ $ F_{12}{}{{=}} F_1 {\mathop{\overset{qp}{\times}}} F_2)$ be a quasi-product observable in ${\overline{\mathcal A}}$. Let $\rho \in {\frak S}^p({\mathcal A}^*) $. Let $\Xi_1$ $ \in {\cal F}_1 $ and $\Xi_2$ $ \in {\cal F}_2$. If it holds that

\begin{align} [{\mathsf O}_{12}^{(1)};{\Xi_1}] \underset{ {\mathsf M}_{{\overline{\mathcal A}}} ({\mathsf O}_{12} , S_{ [\rho] }) }{ \Longrightarrow} [{\mathsf O}_{12}^{(2)};{\Xi_2}] \tag{8.7} \end{align} then we see: \begin{align} [{\mathsf O}_{12}^{(1)};{\Xi_1^c}] \underset{ {\mathsf M}_{{\overline{\mathcal A}}} ({\mathsf O}_{12} , S_{ [\rho] }) }{ \Longleftarrow} [{\mathsf O}_{12}^{(2)};{\Xi_2^c}] \end{align}
Proof. The proof is easy, but we add it. Assume the condition (8.7). That is, \begin{align} {}_{{\mathcal A}^*} \big(\rho, F_{12}{} (\Xi_1 \times (X_2 \setminus \Xi_2)) \big) {}_{\overline{\mathcal A} } = 0 \end{align} Since $\Xi_1 \times \Xi_2{}^c = (\Xi_1^c)^c \times \Xi_2^c $ we see \begin{align} {}_{{\mathcal A}^*} \big(\rho, F_{12}{} ( (\Xi_1^c)^c \times \Xi_2^c) \big) {}_{\overline{\mathcal A} } = 0 \end{align} Therefore, we get \begin{align} [{\mathsf O}_{12}^{(1)};{\Xi_1^c}] \underset{ {\mathsf M}_{{\overline{\mathcal A}}} ({\mathsf O}_{12} , S_{ [\rho] }) }{ \Longleftarrow} [{\mathsf O}_{12}^{(2)};{\Xi_2^c}] \end{align}