The following example may be rather unnatural, but this is indispensable for the well-understanding of dualism.
Example 8.8 [Brain death ]
Consider the classical basic structure
\begin{align}
[C_0(\Omega ) \subseteq L^\infty ( \Omega, \nu ) \subseteq B(L^2 ( \Omega, \nu ))]
\end{align}
Let $\omega_n$ $(\in \Omega=\{\omega_1,\omega_2,\ldots, \omega_N \}$) be the state of Peter. Let ${\mathsf O}_{12}$ $=$ $(X_1 \times X_2 ,$ $ 2^{ X_1 \times X_2 } ,$ $ F_{12}{}{{=}} F_1
{\mathop{\overset{qp}{\times}}}
F_2)$ be the brain death observable in ${L^\infty (\Omega)}$ such that $X_1=\{ T, {\overline T}\}$ $X_2=\{ L, {\overline L}\}$, where $T$ $=$ $\mbox{"think"}$, ${\overline{T}}$ $=$ "not think", $L$ $=$ $\mbox{"live"}$, ${\overline{L}}$ $=$ "not live". For each $\omega_n$ $(n=1,2,\ldots,N)$, ${\mathsf O}_{12}$ satisfies the condition in Table 8.1.
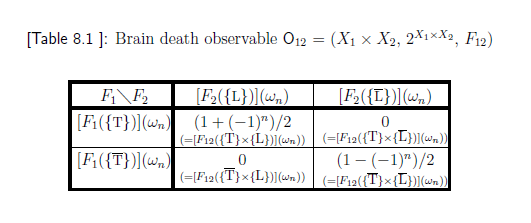
Since $
[F_{12}(
\{ {\mbox{ T}}\}
\times
\{ \overline{\mbox{ L}}\}
)](\omega_n)
=0
$, the following formula holds:
\begin{align}
[{\mathsf O}_{12}^{(1)};{
\{
{\mbox{ T}}
\}
}]
\underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{12} ,
S_{ [\omega_n] }) }{ \Longrightarrow}
[{\mathsf O}_{12}^{(2)};{\{
{{\mbox{ L}}}
\}}]
\end{align}
Of course, this implies that
| $(D_1):$ | $\qquad$ Peter thinks, therefore, Peter lives.
|
This is the same as the statement concerning brain death. In the above example, we see that
| $\quad$ | $\qquad$ observer$\longleftrightarrow$doctor, $\qquad$ system$\longleftrightarrow$Peter,
|

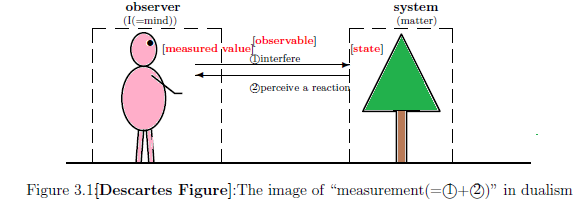
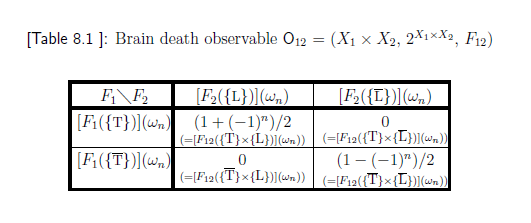
 The above (D$_1$) should not be confused with the following famous Descartes' saying (= cogito proposition):
The above (D$_1$) should not be confused with the following famous Descartes' saying (= cogito proposition):
 Summing up, we want to say the following irony:
Summing up, we want to say the following irony:
