Abstract of Chapter 9
Again recall that, as mentioned in $\S$1.1, the main purpose of this book is to
assert the following figure 1.1:
$(\sharp):$
$
\underset{(=\mbox{ quantum language})}{\mbox{measurement theory}}
\left\{\begin{array}{ll}
\underset{\mbox{($\sharp_1$)}}{
\mbox{pure type}}
\left\{\begin{array}{ll}
\!\!
\mbox{classical system}
:
\mbox{ Fisher statistics}
\\
\!\!
\mbox{ quantum system}
:
\mbox{
usual quantum mechanics
}
\\
\end{array}\right.
\\
\\
\underset{\mbox{($\sharp_2$)}}
{\mbox{mixed type}}
\left\{\begin{array}{ll}
\!\!
\mbox{ classical system}
:
\mbox{including Bayesian statistics, }\\
\qquad
\qquad
\qquad
\qquad
\mbox{Kalman filter}
\\
\!\!
\mbox{ quantum system}
:
\mbox{ quantum decoherence
}
\\
\end{array}\right.
\end{array}\right.
$

In this chapter,
we study
mixed measurement theory,
which includes Bayesian statistics.
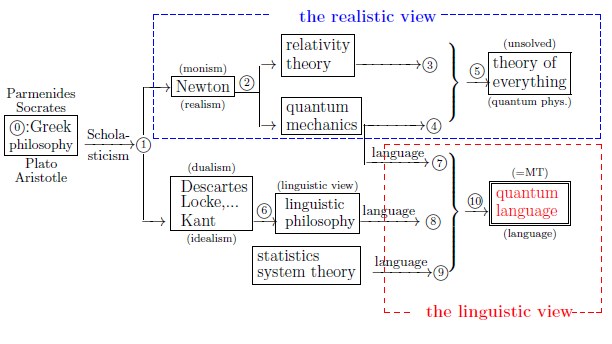
9.0: Mixed measurement theory ($\supset$Bayesian statistics)
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
