EPR's paper: (in $\S$4.4)：

$\bullet$ Einstein, A., Podolosky, B. and Rosen, N.: "Can quantum-mechanical description of reality be considered completely?" Physical Review Ser 2(47), 777--780, (1935)
can can do the various way to read. Although its conclusion is not necessarily clear, but suggestive. This will be shown as follows.

8.7 Syllogism does not hold in quantum systems
Remark 8.15 [Syllogism does not hold in quantum system]

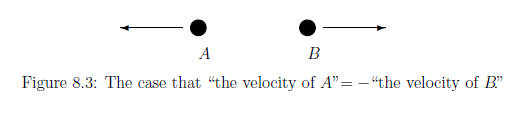
Concerning EPR's paper, we shall add some remark as follows. Let $A$ and $B$ be particles with the same masses $m$. Consider the situation described in the following figure:





The position $q_A$ (at time $t_0$) of the particle A can be exactly measured, and moreover, the velocity of $v_B$ (at time $t_0$) of the particle B can be exactly measured. Thus, we may conclude that

$(A):$the position and momentum (at time $t_0$) of the particle A are respectively and exactly equal to $q_A$ and $- m v_B$ ?

(As mentioned in Section 4.3.3, this is not in contradiction with Heisenberg' uncertainty principle).

However, we have the following question:

\begin{align} \Large{\mbox{Is the conclusion (A) true?}} \end{align}
Now we shall describe the above arguments in quantum system:

A quantum two particles system $S$ is formulated in a tensor Hilbert space $H =H_1 \otimes H_1 = L^2 ({\mathbb R}_{q_1}) \otimes L^2 ({\mathbb R}_{q_2{}}) = L^2 ({\mathbb R}^2_{(q_1 , q_2)})$. The state ${u_0}$ $(\in H =H_1 \otimes H_1 = L^2 ({\mathbb R}^2_{(q_1 , q_2)}))$ $\Big($ or precisely, $\rho_0=| {u_0} \rangle \langle {u_0} | $ $\Big)$of the system $S$ is assumed to be

\begin{align} {u_0} (q_1 , q_2) = \sqrt{ \frac{1}{{{ 2 \pi \epsilon \sigma} }}} e^{ - \frac{1}{8 \sigma^2 } ({q_1 - q_2} - 2{a} )^2 - \frac{1}{8 \epsilon^2 } ({q_1 + q_2} )^2 } \tag{8.18} \end{align}

where a positive number $\epsilon$ is sufficiently small. For each $k=1,2$, define the self-adjoint operators $Q_k{}\! : L^2 ({\mathbb R}^2_{(q_1 , q_2)}) \to $ $L^2 ({\mathbb R}^2_{(q_1 , q_2)}) $ and $P_k \!: L^2 ({\mathbb R}^2_{(q_1 , q_2)}) \to $ $L^2 ({\mathbb R}^2_{(q_1 , q_2)})$ by

\begin{align} & Q_1 = q_1 , \qquad P_1 = \frac{ \hbar \partial }{ i \partial q_1 } \nonumber \\ & Q_2 = q_2 , \qquad P_2 = \frac{ \hbar \partial }{ i \partial q_2 } \tag{8.19} \end{align}
$(\sharp_1):$Let ${\mathsf O}_1=({\mathbb R}^3, {\mathcal B}_{{\mathbb R}^3},F_1)$ be the observable representation of the self-adjoint operator $(Q_1 \otimes P_2 ) \times (I \otimes P_2 )$. And consider the measurement ${\mathsf M}_{B(H)} ({\mathsf O}_1=({\mathbb R}^3, {\mathcal B}_{{\mathbb R}^3},F_1), S_{[|u_0 \rangle \langle u_0|]})$. Assume that the measured value $(x_1, p_2, p_2 ) (\in {\mathbb R}^3 )$. That is, \begin{align} \underset{\mbox{ (the position of $A_1$, the momentum of $A_2$)}}{(x_1, p_2)} \;\; \underset{{\mathsf M}_{B(H)}({\mathsf O}_1,S_{[\rho_0]})}{\Longrightarrow} \;\; \underset{\mbox{ the momentum of $A_2$}}{p_2} \end{align}
$(\sharp_2):$ Let ${\mathsf O}_2=({\mathbb R}^2, {\mathcal B}_{{\mathbb R}^2},F_2)$ be the observable representation of $(I \otimes P_2 ) \times (P_1 \otimes I )$. And consider the measurement ${\mathsf M}_{B(H)} ({\mathsf O}_2=({\mathbb R}^2, {\mathcal B}_{{\mathbb R}^2},F_2), S_{[|u_0 \rangle \langle u_0|]})$. Assume that the measured value $(p_2, -p_2 ) (\in {\mathbb R}^3 )$. That is, \begin{align} \underset{\mbox{ the momentum of $A_2$}}{p_2} \;\; \underset{{\mathsf M}_{B(H)}({\mathsf O}_2,S_{[\rho_0]})}{\Longrightarrow}\;\; \underset{\mbox{ the momentum of $A_1$}}{- p_2} \end{align}
$(\sharp_3):$ Therefore, by $(\sharp_1)$ and $(\sharp_2)$, "syllogism" may say that \begin{align} \underset{\mbox{ the momentum of $A_1$}}{- p_2} \qquad \Big(\mbox{ that is, the momentum of $A_1$ is equal to $-p_2$} \Big) \end{align}
Hence, some may assert that
$(B):$$\color{blue}{{\mbox{The (A) is true}}}$
But, the above argument ( particularly, "syllogism") is not true, thus, \begin{align} {\mbox{The (A) is not true}} \end{align} That is because
$(\sharp_4):$ $ (Q_1 \otimes P_2 ) \times (I \otimes P_2 ) $ and $(I \otimes P_2 ) \times (P_1 \otimes I )$ ( Therefore, ${\mathsf O}_1$ and ${\mathsf O}_2$ ) do not commute, and thus, the simultaneous observable does not exist.
Thus, we can not test the $(\sharp_3)$ experimentally.
Remark 8.16 After all, we think that EPR-paradox says the following two:
$(C_1):$syllogism does not hold in quantum systems,
$(C_2):$there is something faster than light


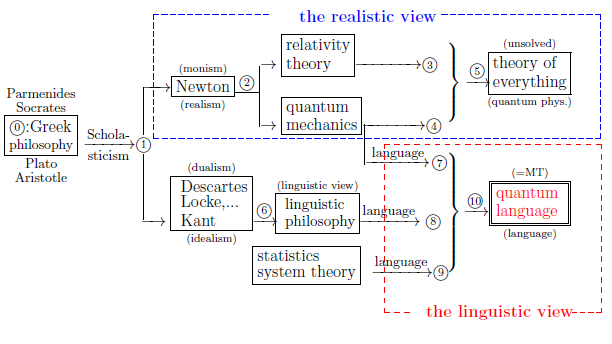$\qquad \quad $ Fig.1.1: The history of world-descriptions

We think that the (C$_1$) is not serious. Thus, we do not need to investigate how to understand the fact (C$_1$). On the other hand, the (C$_2$) is seroius. Although we have to effort to understand the "fact (C$_2$)", this is the problem in physics (i.e., in ⑤ in Figure 1.1). Recall that the spirit of quantum language (i.e., in ⑩ in Figure 1.1) is

"Stop being bothered"