9.3: St. Petersburg two envelope problem
Now, we will review
the St. Petersburg
two envelope problem
(cf.
D.J. Chalmers,
"The St. Petersburg Two-Envelope Paradox,"
Analysis,
Vol.62, 155-157, (2002)).
Define the state space
$\Omega$ such that
$\Omega=\{\omega= 2^k \; |\; k=1,2, \cdots \}$,
with the discrete metric and the counting measure $\nu$.
And define the exact observable
${\mathsf O}=(X, {\mathcal F}, F )$
in $L^\infty(\Omega, \nu )$
such that
Define the mixed state $w$
($\in L^1_{+1}(\Omega, \nu )$, i.e., the probability density function on $\Omega$)
such that
Consider the mixed measurement
${\mathsf M}_{L^\infty (\Omega, \nu )} ({\mathsf O}=(X, {\mathcal F}, F ),
{\overline S}_{[\ast]}(w_0) )$.
Axiom${}^{{\rm (m)}}$ 1(C$_1$)
says that
Note that you knew that A contained $x=2^m$ dollars
(and thus,
$E =\infty > 2^m $).
There is a reason to consider that the switching to $B$ is an advantage.
Remark 9.9
After you get a measured value $2^m$ from the envelope $A$,
you can guess (also see Bayes theorem later) that
the probability density function $w_0$
changes to
the new $w_1$
such that $ w_1 ( 2^m) = 1, w_1 ( 2^k) = 0 ( k \not= m )$.
Thus, now your information about $A:w_1$ and $B:w_0$
is not
symmetrical
(under Bayesian statistics (cf. $\S$9.4)).
Hence, in this case, it is true:
"The Other Person's envelope is Always Greener".
This section is extracted from
the following:
$(\sharp):$
S. Ishikawa;
The two envelopes paradox in non-Bayesian and Bayesian statistics
$\quad$
(
arXiv:1408.4916v4 [stat.OT] 2014
)
You choose randomly (by a fair coin toss) one envelope.
For example,
assume that the envelope is
Envelope A.
And therefore, the host get Envelope $B$.
You find
$2^m$
dollars in the envelope $A$.
Now you are offered the options of keeping A (=your envelope) or switching to B
(= host's envelope ).
What should you do?
$(\sharp):$
a coin was flipped until it came up heads, and if it came up heads on the $k$-th trial, $2^k$ is put into the envelope. This procedure is performed separately for each envelope.

[(P2):Why is it paradoxical?].
You reason that, before opening the envelopes A and B, the expected values
$E(x)$ and $E(y)$ in A and B is infinite respectively.
That is because
\begin{align}
1 \times \frac{1}{2}+ 2 \times \frac{1}{2^2}+ 2^2 \times \frac{1}{2^3}+
\cdots =\infty
\end{align}
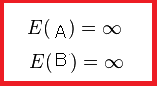 For any $2^m$, if you knew that A contained $x=2^m$ dollars, then the expected value $E(y)$ in B would still be infinite.
Therefore,
you should switch to B. But this seems clearly wrong, as your information about A and B is symmetrical.
This is the famous St. Petersburg two-envelope paradox
(i.e.,
"The Other Person's Envelope is Always Greener"
).
For any $2^m$, if you knew that A contained $x=2^m$ dollars, then the expected value $E(y)$ in B would still be infinite.
Therefore,
you should switch to B. But this seems clearly wrong, as your information about A and B is symmetrical.
This is the famous St. Petersburg two-envelope paradox
(i.e.,
"The Other Person's Envelope is Always Greener"
).
(P2): St. Petersburg two envelope problem:
classical mixed measurement
Therefore,
the expectation of the measured value
is calculated as follows.
\begin{align*}
E= \sum_{k=1}^\infty 2^k \cdot 2^{-k}= \infty
\end{align*}
$(A):$
the probability that a measured value
$
2^k
$
is
obtained by
${\mathsf M}_{L^\infty (\Omega )} ({\mathsf O}=(X, {\mathcal F}, F ),$
$
{\overline S}_{[\ast]}(w_0))$
is given by
$
2^{-k}
$.
$\fbox{Note 9.2}$
There are various criterions except the expectaion.
For example, consider the criterion such that
Under this criterion, it is reasonable to judge that
$$
\begin{cases}
m = 1 &\Longrightarrow \mbox{switching to $B$}
\\
m=2,3,... & \Longrightarrow \mbox{keeping $A$}
\end{cases}
$$
$(\sharp):$
the probability that the switching is disadvantageous" $< \frac{1}{2}$
9.3: St. Petersburg two envelope problem
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
Problem 9.8 [The St. Petersburg two envelope problem]
The host presents you with a choice between two envelopes
(i.e.,
Envelope A
and
Envelope B).
You are told that each of them contains an amount determined by the following procedure, performed separately for each envelope:
