9.10:Bayesian statistics: Monty Hall problem [three prisoners problem]

Problem 9.23[(=Problem9.16Problem})Monty Hall problem (the case that the host throws the dice)].

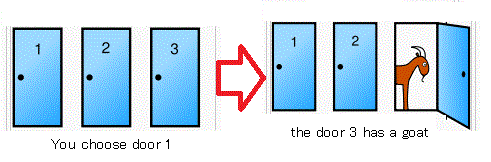
$\quad$

Suppose you are on a game show, and you are given the choice of three doors (i.e., " Door $A_1$"$\!\!\!,\;$ " Door $A_2$"$\!\!\!,\;$ " Door $A_3$"$\!\!)$. Behind one door is a car, behind the others, goats. You do not know what's behind the doors. However, {you pick a door, say "Door $A_1$"}, and the host, who knows what's behind the doors, opens another door, {say " Door $A_3$"$\!\!\!,\;$ which has a goat}. And he adds that $(\sharp_1):$ the car was set behind the door decided by the cast of the (distorted) dice. That is, the host set the car behind Door $A_m$ with probability $p_m$ (where $p_1 + p_2 + p_3 =1$, $ 0 \le p_1 , p_2 , p_3 \le 1 $ $)$. He says to you, " Do you want to pick Door $A_2$?"$\;\;$ Is it to your advantage to switch your choice of doors?

Problem 9.24 [three prisoners problem]

$\quad$

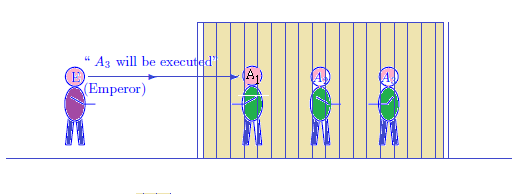
Three prisoners, $A_1$, $A_2$, and $A_3$ were in jail. They knew that one of them was to be set free and the other two were to be executed. They did not know who was the one to be spared, but they know that $(\sharp_2):$ the one to be spared was decided by the cast of the (distorted) dice. That is, Prisoner $A_m$ is to be spared with probability $p_m$ (where $p_1 + p_2 + p_3 =1$, $ 0 \le p_1 , p_2 , p_3 \le 1 $ $)$. but the emperor did know the one to be spared. $A_1$ said to the emperor, "I already know that at least one the other two prisoners will be executed, so if you tell me the name of one who will be executed, you won't have given me any information about my own execution".$\;\;$ After some thinking, the emperor said, "$A_3$ will be executed."$\;\;$ Thereupon $A_1$ felt happier because his chance had increased from $\frac{1}{3(= {\rm Num}[\{A_1,A_2,A_3 \}])}$ to $\frac{1}{2(= {\rm Num}[\{ A_1,A_2 \}])}$. This prisoner $A_1$'s happiness may or may not be reasonable?

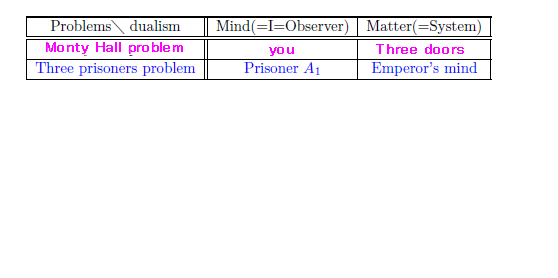
Let $\Omega = \{ \omega_{1} , \omega_{2} , \omega_{3} \}$ be a state space with the discrete metric. Each pure state $\delta_{\omega_{{m}}} (\in {\frak S}^p (C(\Omega)^* ))$ means as follows.

The observable ${\mathsf O}_1$ $\equiv$ $(\{ 1, 2,3 \}, 2^{\{1, 2 ,3\}}, F_1)$ is defined by

Thus we have a mixed measurement ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_1, S_{[{}\ast{}]} ( \nu_0))$. Note that

Here, assume that, by the statistical measurement ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_1, S_{[{}\ast{}]} (\nu_0))$, you obtain a measured value $3$,

which corresponds to the fact that $ \left[\begin{array}{ll} \mbox{the host said "Door $A_3$ has a goat" } \\ \color{blue}{ \mbox{the emperor said "Prisoner $A_3$ is to be executed" } } \end{array}\right] $

Then, Bayes' theorem 9.11 says that the posterior state $\nu_{ post}$ $(\in {\cal M}_{+1}^m (\Omega))$ is given by