This section is extracted from
the following:
9.9: Fisher statistics: Monty Hall problem [three prisoners problem]
$(\sharp):$
S. Ishikawa;
The Final Solutions of Monty Hall Problem and Three Prisoners Problem
arXiv:1408.0963v1 [stat.OT] 2014
so-called isomorphism
But, we think that the meaning of "isomorphism problem" is not clarified, or, it is not able to be clarified without measurement (or, the dualism).
Therefore, in order to understand "isomorphism", we simultaneously discuss the two| $\bullet$ | $ \left\{\begin{array}{ll} \mbox{Monty Hall problem} \\ \color{blue}{\mbox{three prisoners problem}} \end{array}\right. $ |
9.9.1: Fisher statistics: Monty Hall problem [resp. three prisoners problem]
| $\quad$ |
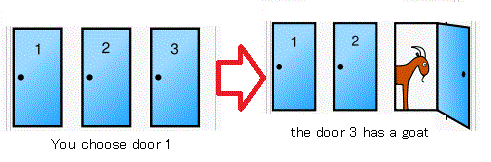
Suppose you are on a game show, and you are given
the choice of three doors
(i.e., " Door $A_1$"$\!\!\!,\;$ " Door $A_2$"$\!\!\!,\;$ " Door $A_3$"$\!\!)$.
Behind one door is a car, behind the others, goats.
You do not know what's behind the doors
However, you pick a door, say "Door $A_1$", and the host, who knows what's behind the doors, opens another door, say " Door $A_3$"$\!\!\!,\;$ which has a goat. He says to you, " Do you want to pick Door $A_2$?"$\;\;$ Is it to your advantage to switch your choice of doors? |
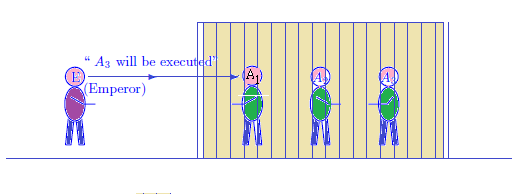
| $\quad$ | Three prisoners, $A_1$, $A_2$, and $A_3$ were in jail. They knew that one of them was to be set free and the other two were to be executed. They did not know who was the one to be spared, but the emperor did know. $A_1$ said to the emperor, "I already know that at least one the other two prisoners will be executed, so if you tell me the name of one who will be executed, you won't have given me any information about my own execution".$\;\;$ After some thinking, the emperor said, "$A_3$ will be executed."$\;\;$ Thereupon $A_1$ felt happier because his chance had increased from $\frac{1}{3(= {\rm Num}\{A_1,A_2,A_3 \}])}$ to $\frac{1}{2(= {\rm Num}\{ A_1,A_2 \}])}$. This prisoner $A_1$'s happiness may or may not be reasonable? |
9.9.2:The answer in Fisher statistics: Monty Hall problem [resp. three prisoners problem]
Let rewrite the spirit of dualism (Descartes figure) as follows.
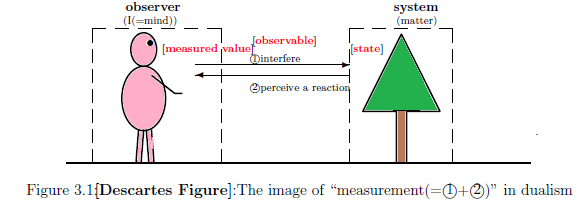
In the dualism, we have the confrontation
\begin{align} \mbox{ "observer$\longleftrightarrow$system" } \end{align} as follows.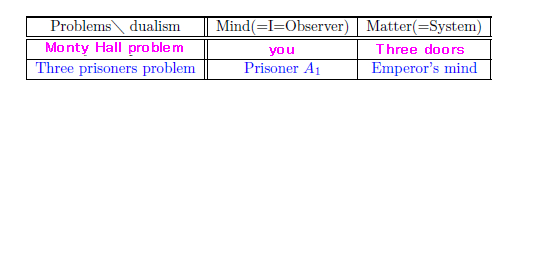
In what follows, we present the first answer to $ \left[\begin{array}{l} \mbox{Problem 9.21 (Monty-Hall problem)} \\ \color{blue}{\mbox{Problem 9.22(Three prisoners problem)}} \end{array}\right] $ in classical pure measurement theory. The two will be simultaneously solved as follows. The spirit of dualism (in Figure 9.7) urges us to declare that
| $(A):$ | $ \left[\begin{array}{l} \mbox{"observer$\;\; \approx\;\; $you" and "system$\;\; \approx\;\; $three doors" in Problem 9.21} \\ \color{blue}{\mbox{"observer$\;\; \approx\;\; $prisoner $A_1$" and "system$\;\; \approx \;\;$emperor's mind" in Problem 9.22}} \end{array}\right] $ |
Put $\Omega = \{ \omega_{1} , \omega_{2} , \omega_{3} \}$ with the discrete topology. Assume that each state $\delta_{\omega_{{m}}} (\in {\frak S}^p (C(\Omega)^* ))$ means
\begin{align} & \left[\begin{array}{ll} &\; \delta_{\omega_{{m}}} \Leftrightarrow \mbox{ the state that the car is } \mbox{behind the door $A_m$} \nonumber \\ \;\;\; & \color{blue}{\mbox{ $ \delta_{\omega_{{m}}} \Leftrightarrow $ } \mbox{ the state that the prisoner $A_m$ is will be executed } } \nonumber \end{array}\right] \nonumber \\ & \qquad \qquad (m=1,2,3 ) \tag{9.28} \end{align}Define the observable ${\mathsf O}_1$ $\equiv$ $(\{ 1, 2,3 \}, 2^{\{1, 2 ,3\}}, F_1)$ in $L^\infty (\Omega)$ such that
\begin{align} & [F_1(\{ 1 \})](\omega_1)= 0.0,\qquad [F_1(\{ 2 \})](\omega_1)= 0.5, \qquad [F_1(\{ 3 \})](\omega_1)= 0.5, \nonumber \\ & [F_1(\{ 1 \})](\omega_2)= 0.0, \qquad [F_1(\{ 2 \})](\omega_2)= 0.0, \qquad [F_1(\{ 3 \})](\omega_2)= 1.0, \nonumber \\ & [F_1(\{ 1 \})](\omega_3)= 0.0,\qquad [F_1(\{ 2 \})](\omega_3)= 1.0, \qquad [F_1(\{ 3 \})](\omega_3)= 0.0, \tag{9.29} \end{align}where it is also possible to assume that $F_1(\{ 2 \})(\omega_1)=\alpha$, $F_1(\{ 3 \})(\omega_1) =1- \alpha$ $ (0 < \alpha < 1)$. Thus we have a measurement ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_1, S_{[{}\ast{}]})$, which should be regarded as the measurement theoretical representation of the measurement that $ \left[\begin{array}{ll} \mbox{ you say "Door $A_1$" } \\ \color{blue}{ \mbox{ "Prisoner $A_1$" asks to the emperor} } \end{array}\right] $.
Here, we assume that
| $(a):$ |
"measured value $1$ is obtained by
the measurement
${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_1, S_{[{}\ast{}]})$"
$ \Leftrightarrow $ $ \left[\begin{array}{ll} \mbox{the host says "Door $A_1$ has a goat" } \\ \color{blue}{\mbox{the emperor says "Prisoner $A_1$ will be executed" } } \end{array}\right] $ |
| (b): |
"measured value $2$ is obtained
by
the measurement
${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_1, S_{[{}\ast{}]})$
"
$ \Leftrightarrow $ $ \left[\begin{array}{ll} \mbox{the host says "Door $A_2$ has a goat" } \color{blue}{\\ \mbox{the emperor says "Prisoner $A_2$ will be executed" } } \end{array}\right] $ |
| (c): |
"measured value $3$ is obtained
by
the measurement
${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_1, S_{[{}\ast{}]})$
"
$ \Leftrightarrow $ $ \left[\begin{array}{ll} \mbox{the host says "Door $A_3$ has a goat" } \\ \color{blue}{\mbox{the emperor says "Prisoner $A_3$ will be executed" } } \end{array}\right] $ |
Recall that $ \left[\begin{array}{ll} \mbox{ the host said "Door 3 has a goat" } \\ \color{blue}{\mbox{ the emperor said "Prisoner $A_3$ will be executed" } } \end{array}\right] $.
This implies that $ \left[\begin{array}{ll} \mbox{you } \\ \color{blue}{\mbox{ Prisoner $A_1$ } } \end{array}\right] $ get the measured value "3" by the measurement ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_1,$ $ S_{[\ast]})$. Note that
\begin{align} & [F_1(\{3\})] (\omega_2) = 1.0 = \max \{ 0.5, \; \; 1.0 , \; \; 0.0 \} \nonumber \\ & = \max \{ [F_1(\{3\})] (\omega_1), [F_1(\{3 \}){}](\omega_2), [F_1(\{3 \})] (\omega_3) \}, \tag{9.30} \end{align}Therefore, Theorem 5.6 (Fisher's maximum likelihood method) says that
| $(B1):$ | In Problem 9.21 (Monty-Hall problem), there is a reason to infer that $[\ast]$ $=$ $\delta_{\omega_2}$. Thus, you should switch to Door $A_2$. |
| (B2): | In Problem 9.22 (Three prisoners problem), there is a reason to infer that $[\ast]$ $=$ $\delta_{\omega_2}$. However, there is no reasonable answer for the question: whether Prisoner $A_1$'s happiness increases. That is, Problem 9.22 is not within Fisher's maximum likelihood method. |
