The wave function collapse( i.e., the projection postulate )

11.2: The wave function collapse ( i.e., the projection postulate )
The lingistic interpretation says that the post measurement state is meaningless. However, considering a tricky measurement, we can realize the wave function collapse. In this section, we shall explain this idea in the following paper:

[4]:	S. Ishikawa, “Linguistic interpretation of quantum mechanics; Projection Postulate” Journal of Quantum Information Science, Vol. 5 No. 4, 2015, pp. 150-155. DOI: 10.4236/jqis.2015.54017 ( download free)

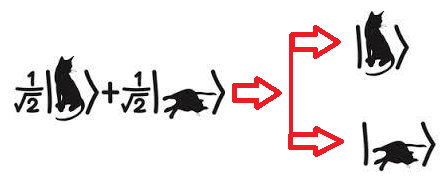
or, Reseach Report; Keio Math [KSTS/RR-15/009](S. Ishikawa ).( download free) ,

11.2.1: Problem: The von Neumann-Lüders projection postulate

Let $[{\mathcal C}(H),B(H)]_{B(H)}$ be a quantum basic structure. Let $\Lambda$ be a countable set. Consider the projection valued observable ${\mathsf O}_P =( \Lambda ,2^{\lambda}, P)$ in $B(H)$. Put

\begin{align} P_{\lambda } = P( \{\lambda \} ) \qquad (\forall \lambda \in \Lambda ) \tag{11.8} \end{align} Axiom1 (measurement; $\S$2.7) says:

(A1):

The probability that a measured value $\lambda_0$ $( \in {\Lambda})$ is obtained by the measurement ${\mathsf{M}}_{B(H)} ({\mathsf{O}}_P$ ${\; :=} ( \Lambda ,2^{\lambda}, P),$ $ S_{[\rho]})$ is given by \begin{align} \mbox{Tr}_{{}_H}( \rho P_{\lambda_0} ) (= \langle u , P_{\lambda_0} u \rangle = \| P_{\lambda_0} u \|^2 ), \quad (\mbox{ where } \rho= |u \rangle \langle u | ) \tag{11.9} \end{align}

Also, the von Neumann-Lüders projection postulate ( in the Copenhagen interpretation) says:

(A$_2$)

When a measured value $\lambda_0$ $( \in {\Lambda})$ is obtained by the measurement ${\mathsf{M}}_{B(H)} ({\mathsf{O}}_P{\; :=} ( \Lambda ,2^{\lambda}, P),$ $ S_{[\rho]})$, the post-measurement state $\rho_{\mbox{ post}}$ is given by \begin{align} \rho_{\mbox{ post}} =\frac{P_{\lambda_0} |u \rangle \langle u |P_{\lambda_0} }{\| P_{\lambda_0} u \|^2} \tag{11.10} \end{align} And therefore, when a next measurement ${\mathsf{M}}_{B(H)} ({\mathsf{O}}_F{\; :=}(X,{\mathcal F}, F),$ $ S_{[\rho_{\mbox{ post}}]})$ is taken (where ${\mathsf{O}}_F$ is arbitrary observable in $B(H)$), the probability that a measured value belongs to $\Xi ( \in {\mathcal F} )$ is given by \begin{align} \mbox{Tr}_{{}_H} ( \rho_{\mbox{post}} F(\Xi )) \Big(= \langle \frac{P_{\lambda_0} u}{\| P_{\lambda_0} u \| }, F(\Xi) \frac{P_{\lambda_0} u}{\| P_{\lambda_0} u \|} \rangle \Big) \tag{11.11} \end{align}

Problem 11.5 In the linguistic interpretation, the phrase:"post-measurement state" in the (A$_2$) is meaningless. Also, the above (=(A$_1$)+(A$_2$)) is equivalent to the simultaneous measurement ${\mathsf M}_{B(H)}({\mathsf{O}}_F \times {\mathsf{O}}_P, S_{[\rho]})$, which does not exist in the case that ${\mathsf{O}}_P$ and ${\mathsf{O}}_F$ do not commute. Hence the (A$_2$) is meaningless in general. Therefore, we have the following problem:

(B)	Instead of the ${\mathsf{O}}_F \times {\mathsf{O}}_P$ in ${\mathsf M}_{B(H)}({\mathsf{O}}_F \times {\mathsf{O}}_P, S_{[\rho]})$, what observable should be chosen?

In the following section, I answer this problem within the framework of the linguistic interpretation.

11.2.2: The derivation of von Neumann-Lüders projection postulate in the linguistic interpretation

Consider two basic structure $[{\mathcal C}(H),B(H)]_{B(H)}$ and $[{\mathcal C}(H \otimes K),B(H \otimes K)]_{B(H \otimes K)}$. Let $\{ P_\lambda \; |\; \lambda \in \Lambda \}$ be as in Section 2.1, and let $\{ e_{\lambda} \}_{\lambda \in \Lambda }$ be a complete orthonormal system in a Hilbert space $K$. Define the predual Markov operator $\Psi_*: Tr(H) \to Tr(H \otimes K)$ by, for any $u \in H$,

\begin{align} \Psi_* (|u \rangle \langle u |) = |\sum_{\lambda \in \Lambda }(P_{\lambda } u \otimes e_{\lambda} )\rangle \langle \sum_{\lambda \in \Lambda }( P_{\lambda } u \otimes e_{\lambda}) | \tag{11.12} \end{align} or \begin{align} \Psi_* (|u \rangle \langle u |) = \sum_{\lambda \in \Lambda } | P_{\lambda } u \otimes e_{\lambda} \rangle \langle P_{\lambda } u \otimes e_{\lambda} | \tag{11.13} \end{align}

Thus the Markov operator $\Psi: B(H \otimes K) \to B(H)$ ( in Axiom 2) is defined by $\Psi = (\Psi_*)^*$.

Define the observable ${\mathsf O}_G = ( {\Lambda}, 2^{\Lambda}, G)$ in $B(K)$ such that

$$ G( \{ \lambda \} ) = |e_{\lambda} \rangle \langle e_{\lambda} | \qquad (\lambda \in \Lambda ) $$

Let ${\mathsf O}_F = (X, {\mathcal F}, F)$ be arbitrary observable in $B(H)$. Thus, we have the tensor observable ${\mathsf O}_F \otimes {\mathsf O}_G$ $=$ $(X \times {\Lambda } ,{\mathcal F} \boxtimes 2^{\Lambda }, F \otimes G )$ in $B(H \otimes K)$, where ${\mathcal F} \boxtimes 2^{\Lambda }$ is the product $\sigma$-field.

Fix a pure state $\rho = |u \rangle \langle u |$ $( u \in H , \| u \|_H = 1 )$. Consider the measurement ${\mathsf M}_{B(H)} (\Psi( {\mathsf O}_F \otimes {\mathsf O}_G), S_{[\rho ]} )$. Then, we see that

(C)	the probability that a measured value $(x, \lambda )$ obtained by the measurement ${\mathsf M}_{B(H)} (\Psi ( {\mathsf O}_F \otimes {\mathsf O}_G),$ $ S_{[\rho ]} )$ belongs to $ \Xi \times\{ \lambda_0 \}$ is given by

\begin{align*} & \mbox{Tr}_{{}_H}[ (|u \rangle \langle u |) \Psi( F(\Xi) \otimes G(\{\lambda_0 \}))] = {}_{{}_{\scriptsize {Tr}(H)}} \big(|u \rangle \langle u |, \Psi( F(\Xi) \otimes G(\{\lambda_0 \}) ) \big)_{{}{B(H)}} \\ = & {}_{{}_{\scriptsize {Tr}(H \otimes K)}} \big(\Psi_* (|u \rangle \langle u |), F(\Xi) \otimes G(\{ \lambda_0 \}) \big)_{{}{B(H \otimes K)}} = \mbox{Tr}_{{}_{H \otimes K }} [ (\Psi_* (|u \rangle \langle u |)) ( F(\Xi) \otimes G(\{\lambda_0 \}) ) ] \\ = & \mbox{Tr}_{{}_{H \otimes K }} [( |\sum_{\lambda \in \Lambda }( P_{\lambda} u \otimes e_{\lambda})\rangle \langle \sum_{\lambda \in \Lambda }( P_{\lambda} u \otimes e_{\lambda}) | ) ( F(\Xi) \otimes |e_{\lambda_0} \rangle \langle e_{\lambda_0} | ) ] \\ = & \langle P_{\lambda_0} u , F(\Xi ) P_{\lambda_0} u \rangle \quad (\forall \Xi \in {\mathcal F} ) \end{align*} ( In a similar way, the same result is easily obtained in the case of (11.13)).
Thus, we see the following.

(D$_1$)

if $\Xi=X$, then \begin{align} \mbox{Tr}_{{}_H} [ (|u \rangle \langle u |) \Psi( F(X) \otimes G(\{\lambda_0 \}) )] = \langle P_{\lambda_0} u, P_{\lambda_0} u \rangle = \| P_{\lambda_0} u \|^2 \tag{11.14} \end{align}

(D$_2$)

in case that a measured value $( x , \lambda )$ belongs to $ X \times \{ \lambda_0 \}$, the conditional probability such that $x \in \Xi$ is given by \begin{align} \frac{\langle P_{\lambda_0} u , F(\Xi ) P_{\lambda_0} u \rangle}{ \| P_{\lambda_0} u \|^2 } \Big( = \langle \frac{P_{\lambda_0} u}{\| P_{\lambda_0} u \| }, F(\Xi) \frac{P_{\lambda_0} u}{\| P_{\lambda_0} u \|} \rangle \Big) \quad (\forall \Xi \in {\mathcal F } ) \tag{11.15} \end{align}

where it should be recalled that ${\mathsf O}_F$ is arbitrary. Also note that the above (i.e., the projection postulate (D)) is a consequence of Axioms 1 and 2.

Considering the correspondence: $\mbox{(A)} \Leftrightarrow \mbox{(D)}$, that is, $$ {\mathsf{M}}_{B(H)} ({\mathsf{O}}_P, S_{[\rho]}) \mbox{ $\Big($or, meaningless $ {\mathsf{M}}_{B(H)} ({\mathsf{O}}_F \times {\mathsf O}_P, S_{[\rho]}) $ $\Big)$ } \Leftrightarrow {\mathsf M}_{B(H)}(\Psi ({\mathsf O}_F \otimes {\mathsf O}_G ), S_{[\rho ]} ), $$ namely, $$ \quad \mbox{(11.9)} \Leftrightarrow \mbox{(11.14)}, \quad \mbox{(11.11)} \Leftrightarrow \mbox{(11.15)} $$

there is a reason to assume that the true meaning of the (A) is just the (D). Also, note the taboo phrase "post-measurement state" is not used in (D$_2$) but in (A$_2$). Hence, we obtain the answer of Problem 11.5 (i.e., $\Psi ( {\mathsf O}_F \otimes {\mathsf O}_G )$ ).

Postulate 11.6 [Projection postulate] In the sense of the (D$_2$), the statement (A$_2$) is often used. That is, we often say:

(E)

Remark 11.7

So called Copenhagen interpretation may admit the post-measurement state. Thus, in this case, readers may think that the post-measurement state is equal to $\frac{P_{\lambda_0} |u \rangle \langle u |P_{\lambda_0} }{\| P_{\lambda_0} u \|^2}$, which is obtained by the (D$_2$) ( since ${\mathsf O}_F$ is arbitrary). However, this idea would not be generally approaved. That is because, if the post-measurement state is admitted, a series of problems occur, that is, "When is a measurement taken?", or "When does the wave function collapse happen?", which is beyond Axioms 1 and 2. Hence, the projection postulate is usually regarded as "postulate". On the other hand, in the linguistic interpretation, the projection postulate is completely clarified, and therefore, it should be regarded as a theorem. Recall the Wittgenstein's words: "The limits of my language mean the limits of my world", or "What we cannot speak about we must pass over in silence."