In this section, we explain de Broglie's paradox
in $B(L^2({\mathbb R}))$
(cf.
$\S$2.10:de Broglie's paradox in $B({\mathbb C}^2)$
).
Putting
${\mathbf q}=(q_1, q_2, q_3 ) \in {\mathbb R}^3 $,
and
consider
Schrödinger equation
(concerning one particle):
where,$m$ is the mass of the particle,
$V$ is a potential energy.
In order to demonstrate in the picture,
regard ${\mathbb R}^3$
as ${\mathbb R}$.
Therefore,
consider the
Hilbert space
$H=L^2({\mathbb R}, dq)$.
Putting
$H_t=H$
$(t \in {\mathbb R})$,
consider the
quantum basic structure:
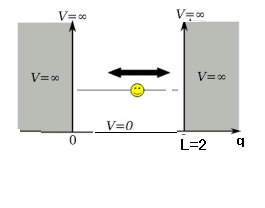
There is a particle $P$
(with mass $m$)
in the box
(that is,
the closed interval $[0,2]
(\subseteq {\mathbb R})$).
Let
$\rho_{t_0}=| \psi_{t_0} \rangle \langle \psi_{t_0}|
\in {\frak S}^p({\mathcal C}(H)^*)$
be an initial state (at time $t_0$) of the particle $P$.
Let
$\rho_t =
| \psi_{t} \rangle \langle \psi_{t}|$
$(t_0 \le t \le t_1 )$
be
a state at time $t$,
where
$\psi_t =\psi(\cdot , t ) \in H = L^2({\mathbb R}, dq)$
satisfies
the following
Schrödinger equation:
Consider the same situation in $\S10.5$,
i.e.,
a particle with the mass $m$ in the box
(i.e.,
the closed interval $[0,2]$)
in the one dimensional space
${\mathbb R}$.
11.3:de Broglie's paradox(non-locality=faster-than-light)
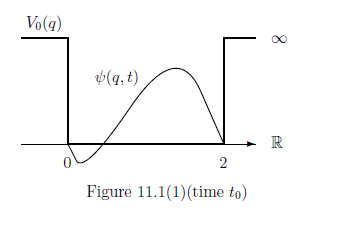
 Equation 11.8 [Schrödinger equation in $\S$10.4.3]
Equation 11.8 [Schrödinger equation in $\S$10.4.3]
Now let us partition the box $[0,2]]$ into $[0,1]]$ and $[1,2]$. That is, we change $V_0 (q) $ to $V_1 (q) $, where
\begin{align} V_1(q) = \left\{\begin{array}{ll} 0 \quad & (0 \le q < 1) \\ \infty \quad & ( q=1) \\ 0 \quad & (1 < q \le 2) \\ \infty & (\mbox{ otherwise }) \end{array}\right. \tag{11.19} \end{align}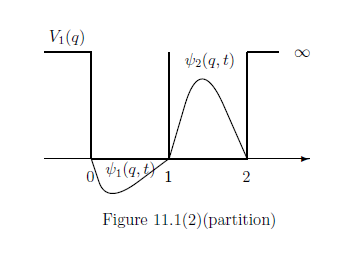
Next, we carry the box $[0,1]$ $\bigl[$resp. the box $[1,2]$ $\!\!\!\bigl]$ to New York (or, the earth) $\bigl[$resp. Tokyo (or, the polar star)$\bigl]$.
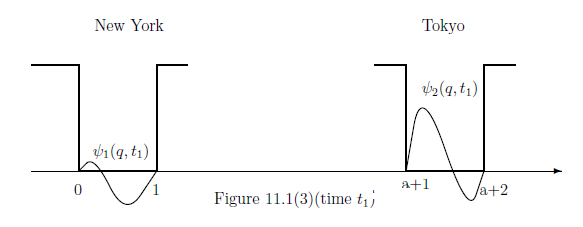
Here, $1 \ll a $. Solving the Schrödinger equation (11.18), we see that
\begin{align} \psi_1(\cdot , t_1) +\psi_2(\cdot , t_1) = U_{t_0,t_1}\psi_{t_0} \end{align}where $U_{t_0,t_1}: L^2({\mathbb R}_{t_1}) \to L^2({\mathbb R}_{t_0})$ is the unitary operator. Define the causal operator $\Phi_{t_0, t_1}: B(L^2({\mathbb R}_{t_2})) \to B(L^2({\mathbb R}_{t_1}))$ by
\begin{align} \Phi_{t_0, t_1}(A) = U_{t_0,t_1}^* A U_{t_0,t_1} \qquad (\forall A \in B(L^2({\mathbb R}_{t_2}))) \end{align}Put $T=\{t_0, t_1\}$. And consider the observable ${\mathsf O} =(X=\{N,T.E\}, 2^X, F)$ in $B(L^2({\mathbb R}_{t_1}))$ (where "N"=New York, "T"=Tokyo, "E"=elsewhere ) such that
\begin{align} & [F(\{N\})](q) = \left\{\begin{array}{ll} 1 \quad & 0 \le q < 1 \\ 0 & \mbox{elsewhere} \end{array}\right., \quad [F(\{T\})](q) = \left\{\begin{array}{ll} 1 \quad & a+1 \le q < a+2 \\ 0 & \mbox{elsewhere} \end{array}\right., \\ & [F(\{E\})](q)=1-[F(\{N\})](q)-[F(\{T\})](q) \end{align} Conclusion 11.9| $(A_1):$ | the probability that a measured value $ \left[\begin{array}{ll} N \\ T \\ E \end{array}\right] $ is obtained by the measurement \\ $ {\mathsf M}_{B(L^2({\mathbb R}_{t_0}))} \Big( \Phi_{t_0,t_1}{\mathsf O}, S_{[|\psi_{t_0} \rangle \langle \psi_{t_0}|]} \Big) $ is given by \begin{align} \left[\begin{array}{ll} \langle u_{t_0} , \Phi_{t_0. t_1} F(\{N\}) u_{t_0} \rangle= \int_0^1 |\psi_1(q , t_1)|^2 dq \\ \langle u_{t_0} , \Phi_{t_0. t_1} F(\{T\})u_{t_0} \rangle = \int_{a+1}^{a+2} |\psi_2(q , t_1)|^2 dq \\ \langle u_{t_0} , \Phi_{t_0. t_1} F(\{E \})u_{t_0} \rangle = 0 \end{array}\right] \end{align} |
Also,
according to Schrödinger picture we see, {Axiom 1 ( measurement: $\S$2.7), that
| $(A_2):$ | the probability that a measured value $ \left[\begin{array}{ll} N \\ T \\ E \end{array}\right] $ is obtained by the measurement \\ $ {\mathsf M}_{B(L^2({\mathbb R}_{t_0}))} \Big( {\mathsf O}, S_{[\Phi_{t_0,t_1}^*(|\psi_{t_0} \rangle \langle \psi_{t_0}|)]} \Big) $ is given by \begin{align} \left[\begin{array}{ll} \mbox{Tr} \Big( \Phi_{t_0,t_1}^*(|\psi_{t_0} \rangle \langle \psi_{t_0}|) \cdot F(\{N\}) \Big) = \langle U_{t_0,t_1} \psi_{t_0} , F(\{N\}) U_{t_0,t_1} \psi_{t_0} \rangle = \int_0^1 |\psi_1(q , t_1)|^2 dq \\ \mbox{Tr} \Big( \Phi_{t_0,t_1}^*(|\psi_{t_0} \rangle \langle \psi_{t_0}|) \cdot F(\{T\}) \Big) = \langle U_{t_0,t_1} \psi_{t_0} , F(\{T\}) U_{t_0,t_1} \psi_{t_0} \rangle = \int_{a+1}^{a+2} |\psi_2(q , t_1)|^2 dq \\ \mbox{Tr} \Big( \Phi_{t_0,t_1}^*(|\psi_{t_0} \rangle \langle \psi_{t_0}|) \cdot F(\{E\}) \Big) = \langle U_{t_0,t_1} \psi_{t_0} , F(\{E\}) U_{t_0,t_1} \psi_{t_0} \rangle = 0 \end{array}\right] \end{align} |
Remark 11.10 In the above, assume that we get a measured value "N", that is, we open the box $[0,1]$ at New York. And assume that we find the particle in the box $[0,1]$. Then, there may be an opinion that quantum mechanics says that at the moment the wave function $\psi_2$ vanishes. That is,
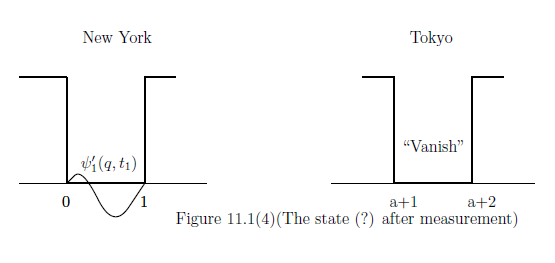
where $$ \psi'_1(q,t_1)= \frac{\psi_1(q,t_1)}{\| \psi'_1(\cdot ,t_1)\|} $$ Thus, we may consider "the collapse of wave function" such as \begin{align} \psi_1(\cdot, t_1) + \psi_2(\cdot, t_1) \xrightarrow[\scriptsize{\mbox{ the collapse of wave function}}]{} \psi'_1(\cdot,t_1) \tag{11.20} \end{align} However, this kind of "the collapse of wave function" is not assured in quantum language (which says that "state does not move" ). In this sense, we consider that
| $\bullet$ | the description (A$_1$) may not be paradoxical, on the other hand, the description (A$_2$) may be somewhat paradoxical |
Also, note that New York $\bigl[$resp. Tokyo$\bigl]$ may be the earth $\bigl[$resp. the polar star$\bigl]$. Thus,
| $\bullet$ | the above argument (in both cases (A$_1$) and (A$_2$)) implies that there is something faster than light. |
This is called " the de Broglie paradox". This is a true paradox, which is not clarified even in quantum language.
