12.1: Finite realized causal observable
In dualism
(i.e.,
quantum language),
Axiom 2 (Causality)
is not used independently.
Axiom 2 (Causality)
is always used with
Axiom 1 (measurement).
That is because

$(A_1):$ To be is to be perceived
(by George Berkeley(A.D. 1685- A.D. 1753))
$\fbox{Note 12.1}$
Note
that Berkeley's words is opposite to
Einstein's words:
in Einstein and Tagore's conversation.
$(\sharp):$
The moon is there whether one looks at it or not.

In this chapter, we devote ourselves to {finite} realized causal observable. ( For the infinite realized causal observable, see Chapter 14.) The readers should understand:
| $\bullet$ | "realized causal observable" is a direct consequence of the linguistic interpretation, that is, \begin{align} \mbox{ only one measurement is permitted } \end{align} |
Now we will review the following theorem:
Theorem 12.1 [=Theorem 11.1Theorem:Causal operator and observable] Consider the basic structure: \begin{align} [ {\mathcal A}_k \subseteq \overline{\mathcal A}_k \subseteq {B(H_k)}] \qquad (k=1,2) \end{align}
Let $\Phi_{1,2}:\overline{\mathcal A}_2 \to \overline{\mathcal A}_1$ be a causal operator, and let $ {\mathsf O}_2$ $=$ $(X , {\cal F} , F_2)$ be an observable in ${\overline{\mathcal A}_2}$. Then, $\Phi_{1,2} {\mathsf O}_2$ $=$ $(X , {\cal F} , \Phi_{1,2} F_2)$ is an observable in ${\overline{\mathcal A}_1}$.
Proof See the proof of Theorem 11.1.
In this section,we consider the case that the {tree} ordered set $T(t_0)$ is finite. Thus, putting $T(t_0) = \{ t_0, t_1,\ldots , t_N \}$, consider the finite tree $(T(t_0), {{\; \leqq \;}})$ with the root $t_0$, which is represented by $(T{{=}} \{ t_0,t_1,\ldots, t_N\} , \pi: T \setminus \{ t_0 \} \to T)$ with the the parent map $\pi$.
Definition 12.2 [(finite)sequential causal observable] Consider the basic structure: \begin{align} [ {\mathcal A}_k \subseteq \overline{\mathcal A}_k \subseteq {B(H_k)}] \qquad (t \in T(t_0)=\{t_0, t_1, \cdots, t_n \}) \end{align}
in which, we have a sequential causal operator $\{ \Phi_{t_1,t_2}{}: $ $\overline{\mathcal A}_{t_2} \to \overline{\mathcal A}_{t_1} \}_{(t_1,t_2) \in T^2_{\leqq}}$ (cf. Definition 10.10 ) such that
| $(i):$ | for each $(t_1,t_2) \in T^2_{\leqq}$, a causal operator $\Phi_{t_1,t_2}{}: $ ${ \overline{\mathcal A}_{t_2}} \to {\overline{\mathcal A}_{t_1}}$ satisfies that $\Phi_{t_1,t_2} \Phi_{t_2,t_3} = \Phi_{t_1,t_3}$ $(\forall (t_1,t_2)$, $\forall (t_2,t_3) \in T^2_{\leqq})$. Here, $\Phi_{t,t} : {\overline{\mathcal A}_{t}} \to {\overline{\mathcal A}_{t}}$ is the identity. |

For each $t \in T$, consider an observable ${\mathsf O }_t {{=}} (X_t, {\cal F}_t , F_t)$ in $\overline{\mathcal A}_{t} $. The pair $[{}\{ {\mathsf O}_t \}_{ t \in T} , \{ \Phi_{t_1,t_2}{}: $ $\overline{\mathcal A}_{t_2} \to \overline{\mathcal A}_{t_1} \}_{(t_1,t_2) \in T^2_{\leqq}}$ $]$ is called a sequential causal observable , denoted by $[{}{\mathsf O}_T{}]$ or $[{}{\mathsf O}_{T(t_0)}{}]$. That is, $[{}{\mathsf O}_T{}]$ $=$ $[{}\{ {\mathsf O}_t \}_{ t \in T} , \{ \Phi_{t_1,t_2}{}: $ $ \overline{\mathcal A}_{t_2} \to \overline{\mathcal A}_{t_1} \}_{(t_1,t_2) \in T^2_{\leqq}}$ $]$. Using the parent map $\pi: T\setminus \{t_0\} \to T$, $[{}{\mathsf O}_T{}]$ is also denoted by $[{}{\mathsf O}_T{}]$ $=$ $[{}\{ {\mathsf O}_t \}_{ t \in T} , $ $ \{ \overline{\mathcal A}_{t} \xrightarrow[]{{\Phi_{ \pi(t), t } }} \overline{\mathcal A}_{\pi(t)} \}_{t \in T \setminus \{ t_0 \}) {}}]$.
Now we can show our present problem.
Problem 12.3 We want to formulate the measurement of a sequential causal observable$[{}{\mathsf O}_T{}]$ $=$ $[{}\{ {\mathsf O}_t \}_{ t \in T} , \{ \Phi_{t_1,t_2}{}: $ $ \overline{\mathcal A}_{t_2} \to \overline{\mathcal A}_{t_1} \}_{(t_1,t_2) \in T^2_{\leqq}}$ $]$ for a system $S$ with an initial state $\rho_{t_0} (\in {\frak S}^p({\mathcal A}_{t_0}^*)) $.
\begin{align} \color{magenta}{ \mbox{ How do we formulate this measurement? } } \end{align}Now let us solve this problem as follows. Note that the linguistic interpretation says that
\begin{align} \mbox{ only one measurement (and thus, only one observable) is permitted} \end{align}Thus, we have to combine many observables in a sequential causal observable$[{}{\mathsf O}_T{}]$ $=$ $[{}\{ {\mathsf O}_t \}_{ t \in T} ,$ $ \{ \Phi_{t_1,t_2}{}: $ $ \overline{\mathcal A}_{t_2} \to \overline{\mathcal A}_{t_1} \}_{(t_1,t_2) \in T^2_{\leqq}}$ $]$. This is realized as follows.
Let $T(t_0) = \{ t_0, t_1,\ldots , t_N \}$ be a {finite} tree. Let $[{\mathsf O}_{T(t_0)}]$ $=$ $[{}\{ {\mathsf O}_t \}_{ t \in T}, \{ \Phi_{\pi(t), t }{}: $ $\overline{\mathcal A}_{t} $ $ \xrightarrow[]{{\Phi_{ \pi(t), t } }} $ $ \overline{\mathcal A}_{\pi(t)} \}_{ t \in T\setminus \{t_0\} }$ $]$ be a sequential causal observable.
For each $s$ $(\in T)$, put $T_s = \{ t \in T \;|\; t {\; \geqq \;}s \}$. Define the observable $\widehat{\mathsf O}_s {{=}} (\times_{t \in T_s } X_t, $ $\boxtimes_{t \in T_s } {\cal F}_t, {\widehat F}_s)$ in $ \overline{\mathcal A}_{s} $ such that
\begin{align} \widehat{\mathsf O}_s = \left\{\begin{array}{ll} {\mathsf O}_s \quad & \mbox{( if $ s \in T \setminus \pi (T) \; $)} \\ \\ {\mathsf O}_s {\times} (\times_{t \in \pi^{-1} (\{ s \})} \Phi_{ \pi(t), t} \widehat {\mathsf O}_t) \quad & \mbox{( if $ s \in \pi (T) \; $)} \end{array}\right. \tag{12.1} \end{align}
(In quantum case,the existence of $\widehat{\mathsf O}_s$
is not always guaranteed).
And further,
iteratively,
we get
the observable
$\widehat{\mathsf O}_{t_0{}}$
$=$
$(\times_{t \in T } X_t, $
$\boxtimes_{t \in T } {\cal F}_t,$
${\widehat F}_{t_0})$
in
$
\overline{\mathcal A}_{t_0}
$.
Put
$\widehat{\mathsf O}_{t_0{}}$
$=$
$\widehat{\mathsf O}_{T(t_0){}}$.
The observable
$\widehat{\mathsf O}_{T(t_0){}}$
$=$
$(\times_{t \in T } X_t, $
$\boxtimes_{t \in T } {\cal F}_t,$
${\widehat F}_{t_0})$
is called the
(finite) realized causal observable
of
the
sequential causal observable$[{}{\mathsf O}_{T(t_0)}{}]$
$=$
$[{}\{ {\mathsf O}_t \}_{ t \in T} ,
\{ \Phi_{\pi(t), t }{}: $
$\overline{\mathcal A}_{t}
\to
\overline{\mathcal A}_{\pi(t)}
\}_{ t \in T\setminus \{t_0\} }$
$]$.
Summing up the above arguments, we have the following theorem:
In the classical case, the realized causal observable $\widehat{\mathsf O}_{T(t_0){}}$ $=$ $(\times_{t \in T } X_t, $ $\boxtimes_{t \in T } {\cal F}_t,$ ${\widehat F}_{t_0})$ always exists.
| $\fbox{Note 12.2}$ | In the above (12.1), the product "$\times$" may be generalized as the quasi-product "$\overset{qp}{\times}$". However, in this note we are not concerned with such generalization. |
Example 12.5 [A simple classical example]
Suppose that a tree $(T \equiv \{ 0, 1, ..., 6, 7 \}, \pi)$ has an ordered structure such that $\pi(1) = \pi(6) = \pi(7) = 0$, $\pi(2) = \pi(5) = 1$, $\pi(3) = \pi(4) = 2$.

Consider a sequential causal observable $[{}{\mathsf O}_T{}]$ $=$ $[{}\{ {\mathsf O}_t \}_{ t \in T} , $ $ \{ {L^\infty (\Omega_{t})} {{\Phi_{ \pi(t), t } }\atop{\rightarrow}} $ $ L^\infty (\Omega_{\pi(t)}) \}_{t \in T \setminus \{ 0 \}) {}}]$. Now, we will construct its realized causal observable $\widehat{\mathsf O}_{T(t_0){}}$ $=$ $(\times_{t \in T } X_t, $ $\boxtimes_{t \in T } {\cal F}_t,$ ${\widehat F}_{t_0})$ in what follows.
Put
\begin{align} \widehat{\mathsf O}_t = {\mathsf O}_t \quad \mbox{ and thus} \quad \widehat{F}_t = {F}_t \quad (t = 3,4,5,6,7). \end{align}First we construct the product observable $\widehat{\mathsf O}_2$ in ${L^\infty (\Omega_2)}$ such as
\begin{align} \widehat{\mathsf O}_2 = (X_2 \times X_3 \times X_4, {\cal F}_2 \boxtimes {\cal F}_3 \boxtimes {\cal F}_4, {\widehat F}_2 ) \quad \mbox{ where } {\widehat F}_2 = F_2 \times (\times_{t=3,4} \Phi_{2,t} {\widehat F}_t) , \end{align}Iteratively, we construct the following:
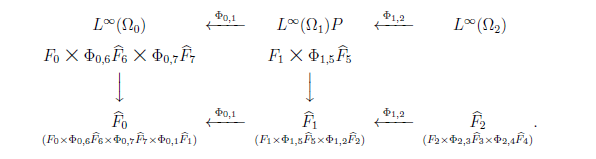
That is, we get the product observable $\widehat{\mathsf O}_1 \equiv ({\times}_{t=1}^5 X_t, {{\boxtimes}_{t=1}^5 {\cal F}_t}, {\widehat F}_1)$ of ${\mathsf O}_1$, $\Phi_{1,2} \widehat{\mathsf O}_2$ and $\Phi_{1,5} \widehat{\mathsf O}_5$, and finally, the product observable
\begin{align} \widehat{\mathsf O}_0 \equiv ({\times}_{t=0}^7 X_t, {{\boxtimes}_{t=0}^7 {\cal F}_t}, {\widehat F}_0 (= F_0 \times (\times_{t=1,6,7} \Phi_{0,t} {\widehat F}_t) ) \end{align}of ${\mathsf O}_0$, $\Phi_{0,1} \widehat{\mathsf O}_1$, $\Phi_{0,6} \widehat{\mathsf O}_6$ and $\Phi_{0,7} \widehat{\mathsf O}_7$.
Then, we get the realization of a sequential causal observable $[{}\{{\mathsf O}_t\}_{t \in T },$ $\{ {L^\infty (\Omega_t)} \overset{\Phi_{\pi(t), t}}\to {L^\infty (\Omega_{\pi(t)})} \}_{ t \in T \setminus \{0\} }{}]$. For completeness, ${\widehat F}_0 $ is represented by
\begin{align} & \widehat{F}_0 (\Xi_0 \times \Xi_1 \times \Xi_2 \times \Xi_3 \times \Xi_4 \times \Xi_5 \times \Xi_6 \times \Xi_7)] \nonumber \\ = & F_0(\Xi_0) \times \Phi_{0,1} \biggl( F_1(\Xi_1) \times \Phi_{1,5}F_5(\Xi_5) \times \Phi_{1,2} \Big( F_2(\Xi_2) \times \Phi_{2,3}F_3(\Xi_3) \times \Phi_{2,4}F_4(\Xi_4) \Big) \biggl) \nonumber \\ & \qquad \qquad \qquad \qquad \times \Phi_{0,6}( F_6(\Xi_6)) \times \Phi_{0,7}( F_7(\Xi_7)) \tag{12.2} \end{align}
(In quantum case,the existence of $\widehat{\mathsf O}_0$ in not guaranteed).
Remark 12.6 In the above example, consider the case that ${\mathsf O}_t$ ($t=2,6,7$) is not determined. In this case,it suffices to define ${\mathsf O}_t$ by the {{}}{existence observable } ${\mathsf O}^{\rm{(exi)}}_t {{=}} (X_t , \{ \emptyset, X_t \}, F^{\rm{(exi)}}_t)$. Then, we see that
\begin{align} & \widehat{F}_0 (\Xi_0 \times \Xi_1 \times X_2 \times \Xi_3 \times \Xi_4 \times \Xi_5 \times X_6 \times X_7 ) \nonumber \\ =& F_0(\Xi_0) \times \Phi_{0,1} \biggl( F_1(\Xi_1) \times \Phi_{1,5}F_5(\Xi_5) \times \Phi_{1,2} \Big( \Phi_{2,3}F_3(\Xi_3) \times \Phi_{2,4}F_4(\Xi_4) \Big) \biggl) \tag{12.3} \end{align}This is true. However, the following is not wrong. Putting $T'=\{0,1,3,4,5 \}$, consider the $[{}{\mathsf O}_{T'}{}]=$ $[{}\{ {\mathsf O}_t \}_{ t \in {T'}} , \{ \Phi_{t_1,t_2}{}: $ ${L^\infty (\Omega_{t_2})} \to {L^\infty (\Omega_{t_1})} \}_{(t_1,t_2) \in (T')^2_{{\; \leqq \;}}}]$.
Then, the realized causal observable $\widehat{\mathsf O}_{T'(0){}}$ $=$ $(\times_{t \in T' } X_t, $ $\boxtimes_{t \in T' } {\cal F}_t,$ ${\widehat F}'_{0})$ is defined by
\begin{align} & \widehat{F}'_0 (\Xi_0 \times \Xi_1 \times \Xi_3 \times \Xi_4 \times \Xi_5 ) = F_0(\Xi_0) \nonumber \\ & \times \Phi_{0,1} \Big( F_1(\Xi_1) \times \Phi_{1,5}F_5(\Xi_5) \times \Phi_{1,4}F_4(\Xi_4)\times \Phi_{1,3}F_3(\Xi_3) \times \Phi_{1,4}F_4(\Xi_4) \Big) \tag{12.4} \end{align}which is different from the true (12.2). We may sometimes omit "existence observable". However, if we do so, we omit it on the basis of careful cautions.
Thus,we can answer Problem 12.3 as follows.
Problem 12.7 [=Problem 12.3](written again) We want to formulate the measurement of a sequential causal observable$[{}{\mathsf O}_T{}]$ $=$ $[{}\{ {\mathsf O}_t \}_{ t \in T} , \{ \Phi_{t_1,t_2}{}: $ $ \overline{\mathcal A}_{t_2} \to \overline{\mathcal A}_{t_1} \}_{(t_1,t_2) \in T^2_{\leqq}}$ $]$ for a system $S$ with an initial state $\rho_{t_0} (\in {\frak S}^p({\mathcal A}_{t_0}^*)) $.
\begin{align} \mbox{ How do we formulate the measurement? } \end{align}Answer If the realized causal observable $\widehat{\mathsf O}_{t_0}$ exists, the measurement is formulated by
\begin{align} \mbox{ measurement } {\mathsf M}_{\overline{\mathcal A}_{t_0}}(\widehat{\mathsf O}_{t_0}, S_{[\rho_{t_0}]}) \end{align}Thus, according to Axiom 1 ( measurement: $\S$2.7), we see that
| $(B):$ | The probability that a measured value $(x_t)_{t \in T}$ obtained by the measurement ${\mathsf M}_{\overline{\mathcal A}_{t_0}}(\widehat{\mathsf O}_{T{}}, S_{[\rho_{t_0}]})$ belongs to ${\widehat \Xi}( \in \boxtimes_{t\in T}{\cal F}_t )$ is given by \begin{align} {}_{{\mathcal A}_0^*} \Big( \rho_{t_0}, {\widehat F}_{t_0} ({\widehat \Xi} ) \Big) {}_{\overline{\mathcal A}_{t_0}} \tag{12.5} \end{align} |
The following theorem, which holds in classical systems, is frequently used.
Theorem 12.8 [The realized causal observable of deterministic sequential causal observable in classical systems]
Let $(T(t_0), {{\; \leqq \;}})$ be a finite tree. For each $t \in T(t_0)$, consider the classical basic structure
\begin{align} [C_0(\Omega_t) \subseteq L^\infty (\Omega_t, \nu_t ) \subseteq B(L^2 (\Omega_t, \nu_t ))] \end{align}Let $[{}{\mathbb O}_T{}]$ $=$ $[{}\{ {\mathsf O}_t \}_{ t \in T} , \{ \Phi_{t_1,t_2}{}: $ ${L^\infty (\Omega_{t_2})} \to {L^\infty (\Omega_{t_1})} \}_{(t_1,t_2) \in T^2_{\leqq}}$ $]$ be deterministic causal observable. Then, the realization $\widehat{\mathsf O}_{{t_0}{}} $ $ \equiv ({\times}_{t \in T} X_t,{{\boxtimes}_{t \in T} {\cal F}_t}, {\widehat F}_{t_0}) $ is represented by
\begin{align} \widehat{\mathsf O}_{{t_0}{}} = \times_{t\in T} \Phi_{{t_0},t} {\mathsf O}_t \end{align}That is, it holds that
\begin{align} & [\widehat{F}_{t_0} ( \times_{t\in T} \Xi_t \ )] (\omega_{t_0} ) = \times_{t\in T} [\Phi_{{t_0},t} {F}_t (\Xi_t )](\omega_{t_0} ) = \times_{t\in T} [{F}_t (\Xi_t )](\phi_{{t_0},t} \omega_{t_0} ) \\ & \quad \qquad \quad \qquad \quad \qquad \quad \qquad (\forall \omega_{t_0} \in \Omega_{t_0}, \forall \Xi_t \in {\cal F}_t ) \end{align}Proof
It suffices to prove the simple classical case of Example 12.5. Using Theorem 10.6 repeatedly, we see that
\begin{align} & {\widehat F}_0 = F_0 \times (\times_{t=1,6,7} \Phi_{0,t} {\widehat F}_t) \\ = & F_0 \times ( \Phi_{0,1} {\widehat F}_1{} \times \Phi_{0,6} {\widehat F}_6{} \times \Phi_{0,7} {\widehat F}_7{} ) = F_0 \times ( \Phi_{0,1} {\widehat F}_1{} \times \Phi_{0,6} {F}_6{} \times \Phi_{0,7} { F}_7{} ) \\ = & \Big( \times_{t=0,6,7} \Phi_{0,t} F_t \Big) \times ( \Phi_{0,1} {\widehat F}_1{} ) = \Big(\times_{t=0,6,7} \Phi_{0,t} F_t \Big) \times \Phi_{0,1} ( F_1 \times (\times_{t=2,5} \Phi_{1,t} {\widehat F}_t) {} ) \\ = & \Big( \times_{t=0,1,6,7}\Phi_{0,t} F_t \Big) \times \Phi_{0,1}(\times_{t=2,5} \Phi_{1,t} {\widehat F}_t) = \Big( \times_{t=0,1,6,7}\Phi_{0,t} F_t \Big) \times \Phi_{0,1}( \Phi_{1,2} {\widehat F}_2{} \times \Phi_{1,5} {\widehat F}_5) \\ = & \Big( \times_{t=0,1,5,6,7}\Phi_{0,t} F_t \Big) \times \Phi_{0,1}( \Phi_{1,2} {\widehat F}_2{} ) = \Big( \times_{t=0,1,5,6,7}\Phi_{0,t} F_t \Big) \times \Phi_{0,1}( \Phi_{1,2} (F_2 \times (\times_{t=3,4} \Phi_{2,t} {\widehat F}_t)) {} ) \\ = & \times_{t=0}^7 \Phi_{0,t} F_t \end{align} This completes the proof.