Abstract ( 13.0: Fisher statistic (II) )
Abstract:
Measurement theory (= quantum language ) is formulated as follows.
\[
\underset{\mbox{ (=quantum language)}}{\fbox{pure measurement theory (A)}}
:=
\underbrace{
\underset{\mbox{ (\(\S\)2.7)}}{
\overset{
[\mbox{ (pure) Axiom 1}]
}{\fbox{pure measurement}}
}
+
\underset{\mbox{ ( \(\S \)10.3)}}{
\overset{
[{\mbox{ Axiom 2}}]
}{\fbox{Causality}}
}
}_{\mbox{ a kind of incantation (a priori judgment)}}
+
\underbrace{
\underset{\mbox{
(\(\S\)3.1)
}}
{
\overset{
{}}{\fbox{Linguistic interpretation}}
}
}_{\mbox{ the manual on how to use spells}}
\]
In Chapter 5 (Fisher statistics (I)),
we discuss "inference" in the relation of "measurement".
In this chapter,
| $(\sharp):$ | S. Ishikawa, Mathematical Foundations of Measurement Theory, Keio University Press Inc. 2006. |
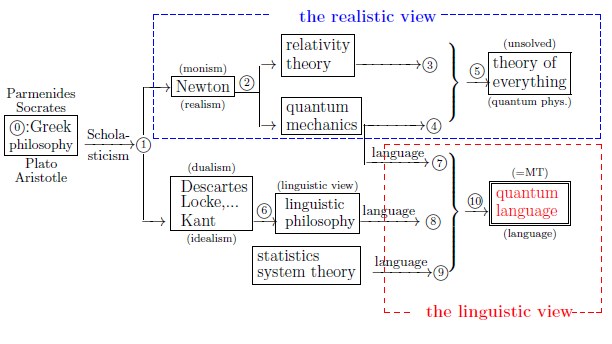
Again recall that, as mentioned in $\S$1.1, the main purpose of this book is to assert the following figure 1.1: