Problem 13.1 [Inference problem and regression analysis]
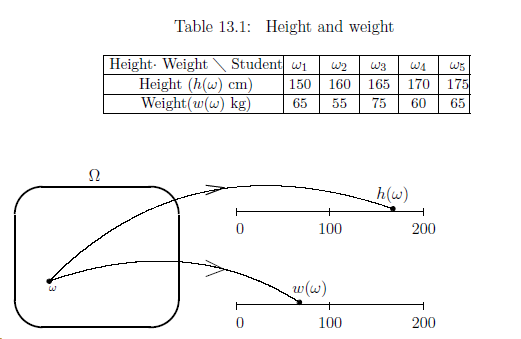
Let $\Omega $
$\equiv$
$\{ \omega_1 , \omega_2 , ... , \omega_{100} \}$
be a set of all students of a certain high school.
Define $h : \Omega \to [{}0, 200{}]$
and
$w : \Omega \to [{}0, 200{}]$
such that:
For simplicity,
put,
$N=5$.
For example,
see
Table 13.1.
13.1: "Inference = Control"
in quantum language
It is usually considered that
\begin{align}
\left\{\begin{array}{ll}
\mbox{$\bullet$ statistics is closely related to inference}
\\
\mbox{$\bullet$ dynamical system theory is closely related to control}
\end{array}\right.
\end{align}
However,
in this chapter,
we show that
\begin{align}
\mbox{
"inference"
=
"control"
}
\end{align}
In this sense,
we conclude that
statistics and dynamical system theory
are essentially the same.
6.1.1: Inference problem(statistics)
Assume that:
| $(a_1):$ | The principal of this high school knows the both functions $h$ and $w$. That is, he knows the exact data of the height and weight concerning all students. |
 Also, assume that:
Also, assume that:
| $(a_2):$ |
Some day, a certain student helped a drowned boy.
But,
he left without reporting the name.
Thus,
all information that the principal knows is as follows:
|
| $(b):$ | Under the above assumption (a$_1$) and (a$_2$), how does the principal infer who is he? |
13.1.2; Control problem(dynamical system theory)
Adding the measurement equation $g: {\mathbb R}^3 \to {\mathbb R}$ to th state equation, we have dynamical system theory (13.2)
. That is, \begin{align} \fbox { dynamical system theory } = \left\{\begin{array}{ll} {\rm{(i)}}: \underset{ (\mbox{initial} \omega(0)=\alpha)}{\frac{d \omega (t)}{dt} = v(\omega(t), t{}, e_1(t), \beta)} \; & \cdots \mbox{(state equation)} \\ \\ {\rm{(ii)}}: x(t) = g(\omega(t), t{}, e_2 (t) ) \; & \cdots \mbox{(measurement)} \end{array}\right. \tag{13.2} \end{align}where $\alpha, \beta $ are parameters, $e_1 (t)$ is noise, $e_2 (t)$ is measurement error.
The following example is the simplest problem concerning inference.
Problem 13.2 [Control problem and regression analysis] We have a rectangular water tank filled with water.
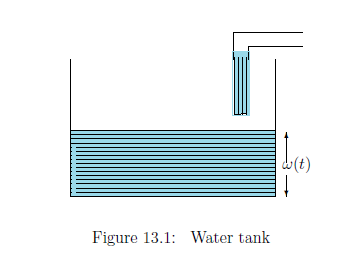
Assume that the height of water at time $t$ is given by the following function $\omega(t)$:
\begin{align} \frac{d\omega}{dt}=\beta_0, \mbox{ then } \omega(t) = \alpha_0 + \beta_0 t, \tag{13.3} \end{align}where $\alpha_0$ and $\beta_0$ are unknown fixed parameters such that $\alpha_0$ is the height of water filling the tank at the beginning and $\beta_0$ is the increasing height of water per unit time. The measured height $x(t)$ of water at time $t$ is assumed to be represented by
\begin{align} x(t) = \alpha_0 + \beta_0 t + e(t), \end{align}where $e(t)$ represents a noise (or more precisely, a measurement error) with some suitable conditions. And assume that as follows:
\begin{align} x(1)=1.9, \quad x(2)=3.0, \quad x(3)=4.7. \tag{13.4} \end{align}Under this setting, we consider the following problem:
| $(c_1):$ | [Control]: Settle the state $(\alpha_0, \beta_0)$ such that measured data (13.4) will be obtained. |
| $(c_2):$ | [Inference]: when measured data (13.4) is obtained, infer the unknown state $(\alpha_0, \beta_0)$. |
Note that \begin{align} \mbox{ (${ c}_1$)=(${ c}_2$) } \end{align} from the theoretical point of view. Thus we consider that
| $(d):$ | Inference problem and control problem are the same problem. And these are characterized as the reverse problem of measurements. |
Remark 13.3 [Remark on dynamical system theory] Again recall the formulation (3.2) of dynamical system theory, in which
| $(\sharp):$ | the noise $e_1 (t)$ and the measurement error $e_2 (t)$ have the same mathematical structure (i.e., stochastic processes ). |
This is a weak point of dynamical system theory. Since the noise and the measurement error are different, I think that the mathematical formulations should be different. In fact, the confusion between the noise and the measurement error frequently occur. This weakness is clarified in quantum language, as shown in Answer 13.6.
