14.2: Is Brownian motion a motion?
14.2.1: Brownian motion in probability theory
There is a reason to consider that
$(A):$
Brownian motion should be understood in measurement theory.
That is because Brownian motion is not in Newtonian mechanics.
As one of applications of Theorem 14.2,
we discuss the Brown motion in quantum language.
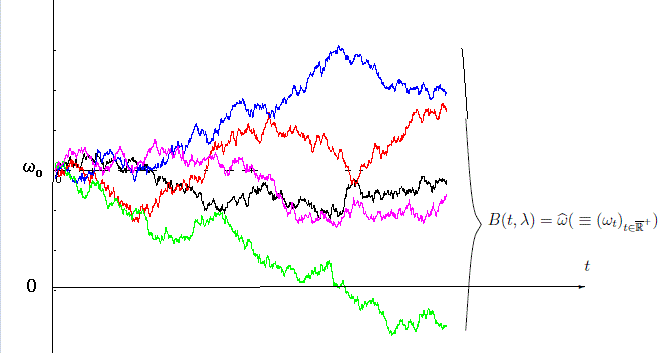
Let us explain the above figure as follows.
Let $(\Lambda, {\cal F}_\Lambda , P)$ be a probability space. For each $\lambda \in \Lambda $, define the real-valued continuous function $B(\cdot ,\lambda): T({{=}} [0, \infty)) \to {\mathbb R}$ such that, for any $t_0=0 < t_1 < t_2 < \cdots < t_n $,
\begin{align} & P(\{ \lambda \in \Lambda \;|\; B(t_k,\lambda) \in \Xi_k \in {\cal B}_{\mathbb R} \;\; (k=1,2,\ldots, n ) \}) \nonumber \\ =& \int_{\Xi_1 } \Big(\cdots (\int_{\Xi_{t_{n-1}}} (\int_{\Xi_{t_n}} \times_{k=1}^{n} G_{ \sqrt{t_{k} - t_{k-1}} } (\omega_{k} - \omega_{k-1}) d\omega_n) d\omega_{n-1}) \cdots \Big) d\omega_1 \tag{14.7} \end{align}
where,
$\omega_0
\in {\mathbb R}$,
$
d\omega_k$
is the Lebesgue measure
on ${\mathbb R}$,
and
$G_{\sqrt{t}}(q)
=
\frac{1}{\sqrt{2\pi t}}\mbox{ exp}\left[{}- \frac{q^2}{2t} \right]$.
The $B(\cdot ,\lambda):
T({{=}} [0, \infty)) \to {\mathbb R}$
is called the
Brownian motion.
14.2.2: Brownian motion in quantum language
Now consider the diffusion equation: \begin{align} \frac{\partial{\rho}_t (q)}{\partial t} = \frac{\partial^2{\rho}_t (q)}{\partial q^2}, \qquad (\forall q \in {\mathbb R}, \forall t \in T {{=}}\overline{\mathbb R}_{+} = [t_0= 0,\infty ) \;) \end{align}
By the solution $\rho_t$, we get predual operator $\{ [{}\Phi_{t_1, t_2}{}]_*$ $:$ $ L^1({\mathbb R} ,dq)$ $\to$ $ L^1({\mathbb R},dq)\}$ as follows. That is, for each $\rho_{t_1} \in L^1({\mathbb R} ,m)$, define
\begin{align} \big([{}\Phi_{t_1, t_2}{}]_{*} ({\rho}_{t_1}) \big) (q) = {\rho}_{t_2}(q) = \int_{-\infty}^{\infty} {\rho}_{t_1}(y) G_{\sqrt{t_2 - t_1} }(q - y) m(dy) \;\; (\forall q \in {\mathbb R}, {}\forall (t_1 , t_2) \in T^2_{\leqq} ) \end{align}For simplicity, we put $(\Omega_t. {\cal B}_{\Omega_t},d \omega_t )=$ $(\Omega, {\cal B}, d \omega)$ $=$ $({\mathbb R}_q, {\cal B}_{{\mathbb R}_q}, dq)$. And thus, for each $t \in T$, consider the classical basic structure:
\begin{align} [C_0(\Omega_t ) \subseteq L^\infty (\Omega_t, d \omega_t) \subseteq B( L^2 (\Omega_t, d \omega_t) )] \end{align}Putting $\Phi_{t_1 , t_2 }$ $=$ $([{}\Phi_{ t_1 , t_2 }{}]_*)^*$, we get the sequential causal operator
\begin{align} \{ \Phi_{ t_1 , t_2 }: L^\infty (\Omega_{t_2}, d \omega_{t_2}) \to L^\infty (\Omega_{t_1}, d \omega_{t_1}) \; | \; (t_1, t_2) \in {T}^2_{{}_{\le}} \} \end{align}For each $t \in T$, consider the exact observable ${\mathsf O}_t^{\scriptsize{\mbox{exa}}} = ( \Omega , {\cal B}_\Omega, F^{\scriptsize{\mbox{exa}}} )$ in $L^\infty( \Omega, d \omega )$. Thus, we get the sequential causal exact observable $[{\mathbb O}_T]$ $ = [\{{\mathsf O}_t^{\scriptsize{\mbox{exa}}} \}_{t\in T} ;$ $ \{ \Phi_{ t_1 , t_2 } \; | \; (t_1, t_2) \in {T}^2_{{}_{\le}} \} ]$. The existence theorem of the infinite classical realized causal observable (Theorem 14.2) says that ${\mathbb O}_T$ has the realized causal observable $\widehat{\mathsf O}_{t_0}$ $=$ $({\Omega}^T, {\cal B}({\Omega}^T), \widehat{F}_{t_0} )$ in $L^\infty ( \Omega ,d \omega )$.
Assume that
| $(B):$ | $\quad$ a measured value ${\widehat \omega}$ $(=(\omega_t)_{t\in T } \in\Omega^{T })$ is obtained by ${{\mathsf M}}_{L^\infty(\Omega) } (\widehat{\mathsf O}_{ t_0 },$ $ S_{[\delta_{\omega_0}]} )$. |
Let ${T'}= \{t_0, t_1,t_2,\cdots,t_n\}$ be a finite subset of $T$, where $t_0=0 < t_1 < t_2 < \cdots < t_n $. Put ${\widehat\Xi}=\Large{\mbox{ $\times$}}_{t\in T }^{T'}\Xi_t$ $\bigl(\in{\cal B}^{ {\overline{\mathbb R}^+} }\bigl)$ where $\Xi_t=\Omega$ $(\forall t\notin {T'})$. Then, by Axiom 1 (measurement; $\S$2.7), we see
| $\quad$ | $\quad$ the probability that ${\widehat \omega} (=(\omega_t)_{t \in T}) $ belongs to the set ${\widehat\Xi} \equiv \Large{\mbox{ $\times$}}_{t\in {T} }^{T'}\Xi_t$ is given by $ [\widehat{F}_{t_0}( \Large{\mbox{ $\times$}}_{t\in {T} }^{T'} \Xi_t )](\omega_0) $ |
where
\begin{align} & [\widehat{F}_{t_0}( \Large{\mbox{ $\times$}}_{t\in {T} }^{T'} \Xi_t )](\omega_0) \nonumber \\ = & \Big(F(\Xi_{0}) \Phi_{ 0 , t_1 } \Big(F(\Xi_{t_1}) \cdots \Phi_{ t_{n-2} , t_{n-1}} \Big( F(\Xi_{t_{n-1}}) \bigl(\Phi_{t_{n-1} , t_n} F(\Xi_{t_n} ) \bigl) \Big) \cdots \Big) (\omega_0) \nonumber \\ =& \int_{\Xi_1 } \Big(\cdots (\int_{\Xi_{t_{n-1}}} (\int_{\Xi_{t_n}} {\times}_{k=1}^{n} G_{ \sqrt{t_{k} - t_{k-1}} } (\omega_{k} - \omega_{k-1}) d\omega_n) d\omega_{n-1}) \cdots \Big) d\omega_1 \tag{14.8} \end{align}
which is equal to
the
(14.7).
Thus, we see that
| $\fbox{Note 14.1}$ |
Thus, the following assertion has a reason in some sense:
|
