Abstract (16.0: Kalman filter) The Kalman filter is located as in the following $(\sharp)$:
$ (\sharp): \mbox{Statistics} \left\{\begin{array}{l} \mbox{Fisher's maximum likelihood method} &{\;} \xrightarrow[\scriptsize{\mbox{ usually deterministic}}]{\scriptsize{\mbox{ $+$ causality}}} \mbox{regression analysis} \\ \\ \mbox{Bayes' method} & {\;} \xrightarrow[\scriptsize{\mbox{ non-deterministic}}]{\scriptsize{\mbox{ $+$ causality}}} \mbox{Kalman filter} \end{array}\right. $
Thus, I can not emphasize too much the importance of the Kalman filter. Though Kalman filter belongs to Bayes' statistics, this fact may not be a common sense. This present state is due to the confusion between Fisher's statistics and Bayes' statistics. I hope that such confusion should be clarified by the above $(\sharp)$ (based on quantum language). This chapter is extracted from the following paper:
| $(\sharp):$ | S. Ishikawa, K. Kikuchi: Kalman filter in quantum language, |
| $(\sharp):$ | S. Ishikawa, Mathematical Foundations of Measurement Theory, arXiv:1404.2664 [math.ST] |
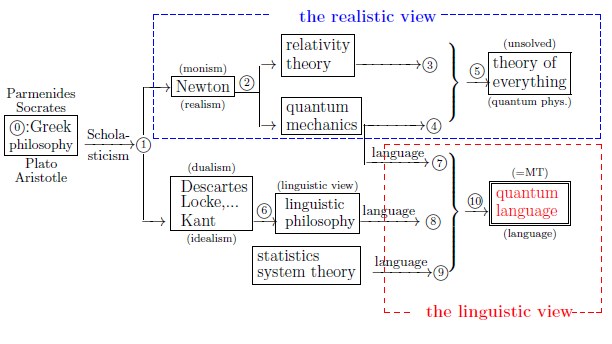
Again recall that, as mentioned in $\S$1.1, the main purpose of this book is to assert the following figure 1.1: