物理学者(実在的科学観)は科学者の中では少数派であって、ほとんどの科学者が言語的科学観の傘下にある。
しかし、実在的科学観はシンプルで、 たとえば、ニュートンとかマックスウェルやアインシュタインが偉いに決まっている。
一方、言語的科学観の方は、すっきりしない。量子言語の観点からすると、統計学ではフィッシャーの最尤法が最も基本的な仕事である.
一言で言えば、
$$
\left\{\begin{array}{l}
\mbox{古典力学(実在的科学観)}\cdots \textcolor{red}{\mbox{ニュートンの運動方程式}}
\\
\\
\mbox{統計学(言語的科学観)}\cdots \textcolor{red}{\mbox{フィッシャーの最尤法}}
\end{array}\right.
$$
と考えてよい。
本節では,統計学の基本である「フィッシャーの最尤法」を言語ルール1($\S$2.7:測定)の言葉遣いで表現する.
フィッシャーの最尤法の説明のために,
次の問題
から始める.
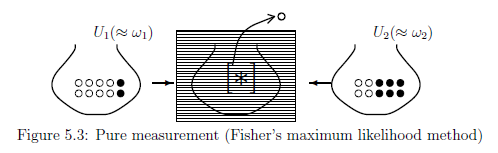
2つの壷 $U_1$と$U_2$がある.
壷 $U_1$には,
$8$個の白球と$2$個の黒
球が入っている.
また,壷 $U_2$には,
$4$個の白球と$6$個の黒
球が入っていると仮定する.
解答
解答は簡単で,
誰もが,「カーテンの後ろの壷は$U_1$である」
と
直感
で答えるだろう.
なぜならば,
通常の統計学の本は、出だし(
確率論の初歩とか様々な分布とか
)が面白いとは言えない。
面白く読むためには、
思い込んで、「確率論の初歩とか様々な分布とか」をスキップして、最重要な「フィッシャーの最尤法」を最初に理解することだと思う。
しかし、信じられないことだが、統計学の本の中には、フィッシャーの最尤法に触れていないものもある。
書いてあっても、本の後半に書いてあることもある。
古典力学の本に、ニュートンの運動方程式が書かれていなかったとすれば、誰もが驚くと思うが...
このような混乱を見ると、著者は
と思ってしまう。
5.2.1: フィッシャーはボルンの逆を考えた
次の手続き
(i)と(ii)を考える.
$\mbox{(i):}$
2つの壷(すなわち, $U_1$ または $U_2$)のうち一つ
が選ばれて,
カーテンの後ろに置かれている.
しかし, カーテンの後ろ
の壷がどちらなのか($U_1$ または $U_2$)をあなたは知らない.
$\mbox{(ii):}$
手続き (i)で選ばれて,カーテンの後ろに置かれた壷の中から
一つの球を取り出す.
そして,その球が白球であった.
ここで,次の問題:
を考えたい.
$\mbox{(iii):}$
手続き(i)では,
どちらの壷($U_1$ または $U_2$)
がカーテンの後ろに置かれたのだろうか?
からである.
簡単すぎて、 「小学生でもわかる理屈」 かもしれないが, この直感の数量的表現が フィッシャーの最尤法 である.
5.2.2: フィッシャーの最尤法 in 測定理論
次の記法から始める:
| $(A_1):$ | 測定${\mathsf M}_{\overline{\mathcal A}} $ $({\mathsf O} {{=}} (X, {\cal F}, F),$ $ S_{[\rho]}{})$を行う多くの場合は, 状態 $\rho \;(\in {\frak S}^p({\mathcal A}^*))$を未知と仮定することは自然である. |
| $(A_2):$ | 通常は,「状態$\rho$を知る」ために測定 ${\mathsf M}_{\overline{\mathcal A}} ({\mathsf O}, S_{[\rho]})$ を 行う |
| $(A_3):$ |
|
この記法${\mathsf M}_{\overline{\mathcal A}} ({\mathsf O}, S_{[*]})$を使って, 我々の当面の問題は,次のように書ける:
| $(a):$ | 測定 ${\mathsf M}_{\overline{\mathcal A}}({\mathsf O} {{=}} (X, {\cal F}, F), S_{[*]}(\!(K)\!) )$ により得られた測定値が $\Xi (\in {\cal F})$ に属したと仮定する. このとき,未知の状態$[*] \;(\in \Omega)$ を推定せよ. |
| $(b):$ | 測定 ${\mathsf M}_{\overline{\mathcal A}}({\mathsf O} {{=}} (X \times Y, {\cal F} \boxtimes {\cal G}, H), S_{[*]}(\!(K)\!) )$ により得られた測定値$(x,y)$が $\Xi \times Y$ $(\Xi \in {\cal F})$ に属したことがわかったとする. このとき, $y \in \Gamma $である確率 を推定せよ. |
したがって,測定 は,,
| $(B):$ | $ \begin{cases} \mbox{表から見れば, $ \quad (観測量[{\mathsf O}],状態[\omega(\in \Omega)]) \xrightarrow[{\mathsf M}_{\overline{\mathcal A}}({\mathsf O}, S_{[\delta_\omega]})]{ \quad \textcolor{red}{測定} \quad} 測定値{[x (\in X)]} $} \\ \\ \mbox{裏から見れば, $ \quad (観測量[{\mathsf O}],測定値[x \in \Xi ( \in {\cal F})]) \xrightarrow[{\mathsf M}_{\overline{\mathcal A}}({\mathsf O}, S_{[\ast]})]{ \quad \textcolor{red}{推定} \quad} 状態{[\omega (\in \Omega)]} $ } \end{cases} $ |
- 推定は,測定の逆問題
推定問題(問題5.4)に答えるために, フィッシャーの最尤法を 測定理論の言葉で表現する.
証明
$\rho_1$と$\rho_2$を$K$の元として,
$\rho_1(H(\Xi \times Y)) <\rho_2(H(\Xi \times Y)) $
と仮定する.
言語ルール1(測定: $\S$2.7)より,
| $\mbox{(i):}$ | 測定${\mathsf M}_{\overline{\mathcal A}} ({\mathsf O}, S_{[\rho_1]})$ により得られる測定値$(x,y)$が $\Xi \times Y$に属する 確率は $\rho_1(H(\Xi \times Y)) $ |
| $\mbox{(ii):}$ | 測定${\mathsf M}_{\overline{\mathcal A}} ({\mathsf O}, S_{[\rho_2]} )$ により得られる測定値$(x,y)$が $\Xi \times Y$に属する 確率は $\rho_2(H(\Xi \times Y)) $ |
となる. $\rho_1(H(\Xi \times Y)) <\rho_2(H(\Xi \times Y)) $ と仮定したのだから, 「(i)は(ii)より稀に起きる」と言える. よって,$[*]=\rho_1$ と推定するより, $[*]=\rho_2$ と推定した方が 理がある. したがって, (5.7)式の $\rho_0$は一理ある. ${\mathsf M}_{\overline{\mathcal A}} ({\mathsf O}, S_{[\rho_0]} )$ によって得られた測定値$(x,y)$が$\Xi \times \Gamma $に属している確率は $\rho_0 ( H( \Xi \times \Gamma ) ) $ なのだから,条件付き確率によって, 定理を得る.

定理 5.6: フィッシャーの最尤法(古典系の場合)
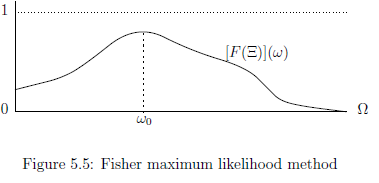
(i): 測定 ${\mathsf M}_{{L^\infty (\Omega) }}({\mathsf O} $ ${{=}} (X, {\cal F}, F),$ $ S_{[*]} (\!( K )\!))$ により得られた測定値 が $\Xi \;(\in {\cal F})$ に属していることがわかったとする. このとき,システム$S$の 未知の状態 $[*]$ を次のような状態 $\omega_0 \;(\in K \subseteq \Omega)$ と推定することには一理ある: \begin{align} [F(\Xi)](\omega_0) = \max_{\omega \in K} [F(\Xi)](\omega) \tag{5.8} \end{align} すなわち, $[F(\Xi)](\omega ) {{\; \leqq \;}}[F(\Xi)](\omega_0)$ $(\forall \omega \in K)$ を満たす$\omega_0 (\in K)$ と推定できる.
(ii):
測定
${\mathsf M}_{{L^\infty (\Omega) }}({\mathsf O} $
${{=}} (X, {\cal F}, F),$
$ S_{[*]} (\!( K )\!))$
により得られた測定値
$x_0 \;(\in {X})$
が得られたとする.
尤度関数$f(x,\omega)$を
\begin{align}
f(x, \omega) = \inf_{\omega_1 \in K}\Big[ \lim_{\Xi \ni x, [F(\Xi)](\omega_1) \not= 0,
\Xi \to \{x\} } \frac{[F(\Xi)](\omega )}{[F(\Xi)](\omega_1 )}
\Big]
\tag{5.9}
\end{align}
と定めて,
$f(x_0,\omega_0)=1$を満たす状態$\omega_0 (\in K)$と推定することは一理ある.
証明$\;\;$ 定理5.5で, \begin{align*} [{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)] = [C_0(\Omega ) \subseteq L^\infty (\Omega ) \subseteq B( L^2 (\Omega ) ] \end{align*} として, ${\mathsf M}_{L^\infty(\Omega ) }({\mathsf O} {{=}} (X \times Y, {\cal F} \boxtimes {\cal G}, H), S_{[*]}(\!(K)\!) )$において, \begin{align*} & 固定された{\mathsf O}_1 {{=}} (X , {\cal F}, F ), \;\; 任意の{\mathsf O}_2 {{=}} (Y, {\cal G}, G), \;\; \\ & {\mathsf O} {{=}}{\mathsf O}_1 \times {\mathsf O}_2 =(X \times Y, {\cal F} \boxtimes {\cal G}, F \times G),\;\; \rho_0 = \delta_{\omega_0} \end{align*} の場合を考える. このとき, \begin{align} P(\Gamma ) = \frac{ [H(\Xi)](\omega_0) \times [G(\Gamma)](\omega_0)}{ [H(\Xi)](\omega_0) \times [G(Y)](\omega_0)} = [ G(\Gamma )](\omega_0) \quad( \forall \Gamma \in {\mathcal G} ) \tag{5.10} \end{align} となり, しかも ${\mathsf O}_2 $は任意だから. 「$[*]=\delta_{\omega_0}( \underset{\mbox{ 同一視}}{\approx} \omega_0)$」 と推定することは 理がある.
| $\fbox{注釈5.1}$ |
この定理の意味は「非常に難しい」と思う.
言語的解釈では, 「測定後の状態はナンセンス」なのだから,
|
カーテンの後ろの壷から球を一つ取り出したら,白球だった.
このとき,壷は$U_1$または$U_2$のどちらか?$\;\;$これを推定せよ.
解答
測定 ${\mathsf M}_{{L^\infty (\Omega) }} ({\mathsf O} {{=}}$ $ ( \{ 白,$ $ 黒 \},$ $ 2^{\{ 白, 黒 \} } ,$ $ F{}) , S_{ [{}{\ast}]}{})$ を考える.ここで, $C(\Omega{})$内の観測量 ${\mathsf O}_{白黒} = ( \{ 白, 黒 \}, 2^{\{ 白, 黒 \} } , F_{白黒}{})$ を次のように定義する: \begin{align} & [F_{白黒}(\{ 白 \}{})](\omega_1{})= 0.8, & \quad & [ F_{白黒}(\{ 黒 \}{})](\omega_1{})= 0.2 \nonumber \\ & [F_{白黒}(\{ 白 \}{})](\omega_2{})= 0.4, & \quad & [F_{白黒}(\{ 黒 \}{})] (\omega_2{})= 0.6 \tag{5.11} \end{align} これより, \begin{align*} & \max \{[F_{白黒}(\{白\})](\omega_1), [F_{白黒}(\{白\})](\omega_2) \} \\ = & \max \{0.8, 0.4\} = 0.8 = F_{白黒}(\{白\})](\omega_1) \end{align*}
 よって,定理5.6により,
状態$\omega_1$が推定できて,
したがって,
カーテンの後ろの壷は$U_1$
であることが推定できる.
よって,定理5.6により,
状態$\omega_1$が推定できて,
したがって,
カーテンの後ろの壷は$U_1$
であることが推定できる.
| $\fbox{注釈5.2}$ |
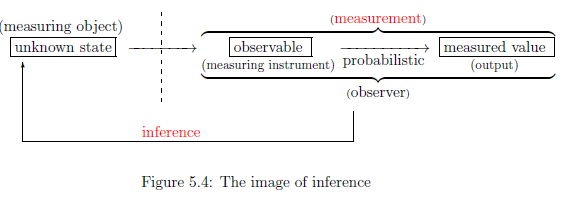
図5.4のように,
測定の逆問題は,推定(フィッシャーの最尤法)であった.
それならば,
逆問題をフィッシャーが解いたのだから,
|