さて、
例 5.1
日本人全男性とアメリカ人全男性の身
長の確率密度関数をそれぞれ,$f_J$と$f_A$とする.
すなわち,
さて,この日常言語の文言(A$_1$)と(A$_2$)を測定理論
の
言葉遣いで記述することを考える.
$\Omega = \{ {\omega}_J , {\omega}_A
\}$
として,
離散距離空間$(\Omega, d_D)$を考えて,
可換$C^*$代数$C_0(\Omega)$を得る.
すなわち,
として, 次の同一視を考える
(したがって,図5.1のような状況を考える):
$L^\infty (\Omega{})$内の観測量
${\mathsf O}_{身長} = ( {\mathbb R}, {\mathcal B} , F_{身長}{})$
は(A)で定義したので,
測定
${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{身長} ,
S_{ [{}{\delta_{\omega}}]}{})$
$(\omega \in \Omega =\{\omega_J, \omega_A \})$
を得る.
よって,上述の(A)
((A$_1$)と(A$_2$))は,
測定理論の言葉で次のように記述できる:
標準偏差$\sigma >$を固定して,
可換$C^*$代数$C_0(\Omega)$において,
$\Omega$
$(={\mathbb R}:実数全体)$
を状態空間とする.
すなわち,
を得る.
測定値空間$X$も
${\mathbb R}$
として,
$L^\infty ({\Omega}{})$
内の
正規観測量
${\mathsf O}_{G_\sigma} $
${{=}}$
$(X(={}{\mathbb R}) , {\cal B}_{{\mathbb R}}^{} ,
G_{\sigma}{})$
を,
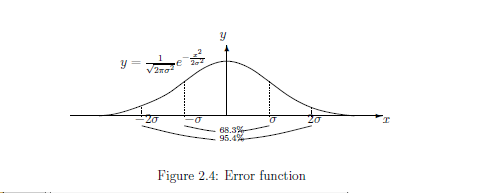
誤差関数(図5.2=図2.4)
を用いて,
次のように定義する:
ここに,${\cal B}_{\mathbb R}$はボレル集合体
とする.
このとき,
たとえば,
$L^\infty (\Omega^n)$内の並列観測量
$\bigotimes_{k=1}^n {\mathsf O}_{G_\sigma}$
$=$
$({\mathbb R}^n, {\mathcal B}_{{\mathbb R}^n}, \bigotimes_{k=1}^n {G_\sigma})$
を考えて,これを
に制限する. これは,
$L^\infty (\Omega)$内の同時観測量
${\mathsf O}^n$
$=$
$({\mathbb R}^n, {\mathcal B}_{{\mathbb R}^n}, {{{\times}}}_{k=1}^n {G_\sigma})$
を考えることと等しい.
すなわち,
ここに,${\cal B}_{\mathbb R}$はボレル集合体
とする.
このとき,$(x_1,x_2, \cdots, x_n )\in X^n (={\mathbb R}^n )$として,
として,
写像$\psi:{\mathbb R}^n \to {\mathbb R}$を
と定めて,
$L^\infty ({\mathbb R} )$内の観測量
${\mathsf O}_{T_n^\sigma} $
${{=}}$
$(X(={}{\mathbb R}) , {\cal B}_{{\mathbb R}}^{} ,
T_n^\sigma{})$
を
で定義しよう.${\mathsf O}_{T_n^\sigma} $
${{=}}$
$(X(={}{\mathbb R}) , {\cal B}_{{\mathbb R}}^{} ,
T_n{})$を$L^\infty({\mathbb R} )$内の
スチューデントの$t$-観測量(or, スチュウデントの$t_n$-観測量)
と言う.
ここで,
と表現できる.
右辺を見ればわかることであるが,$\omega$や$\sigma$に依存しない.
また,
なので,
$n$が$30$以上ならば,$N(0,1)$(
すなわち,平均値$0$,標準偏差$1$の正規分布)
と考えてもよい.
統計学は著者の専門外であるが、次の二つの両立は不思議と思う。
なのだから、
と考えるのは自然である。
この章では、これについて述べる。
5.1.1 母集団(=システム)$\leftrightarrow$パラメター(=状態)
$(A_1):$
日本人男性全体(母集団$\leftrightarrow \omega_J$)から無作為に一人選んで,
その人の身長が,身長が$\alpha$(cm)から$\beta$(cm)までの
確率は,
\begin{align*}
[F_{身長}([\alpha, \beta))](\omega_J)
=\int_\alpha^\beta f_J(x) dx
\end{align*}
である.
$(A_2):$
アメリカ人男性全体(母集団$\leftrightarrow \omega_A$)から無作為に一人選んで,
その人の身長が,身長が$\alpha$(cm)から$\beta$(cm)までの
確率は,
\begin{align*}
[F_{身長}([\alpha, \beta))](\omega_A)
=\int_\alpha^\beta f_A(x) dx
\end{align*}
である.
を得る.
ここで,
\begin{align*}
\nu(\{\omega_J \})=1,
\;\;
\nu(\{\omega_A \})=1
\quad
\end{align*}
$\Big(\text{注意:もちろん,}
\nu(\{\omega_J \})=a,
\;\;
\nu(\{\omega_A \})=b
\;\;
(a,b >0)
\mbox{でもよい}
\Big)$.
また, 純粋状態空間は
\begin{align*}
{\frak S}^p (C_0(\Omega)^*)= \{ \delta_{\omega_J} , \delta_{\omega_A} \}
\approx
\{ {\omega}_J , {\omega}_A
\}
=
\Omega
\end{align*}
となる.
ここで, ,
\begin{align*}
&
\delta_{\omega_J} \quad \cdots \quad
\text{"日本人全男性の集合$U_1$(母集団)の状態"},
\qquad
\\
&
\delta_{\omega_A} \quad \cdots \quad
\text{"アメリカ人全男性の集合$U_2$(母集団)の状態"},
\end{align*}

したがって、次の翻訳を得る:
\begin{align*}
\underset{\mbox{(日常言語)}}{\fbox{文言(A)}}
\xrightarrow[{\mbox{翻訳}}]{}
\underset{\mbox{(量子言語)}}{\fbox{文言(B)}}
\end{align*}
$(B):$
測定
$
\left[\begin{array}{ll}
{\mathsf M}_{{L^\infty (\Omega)}} ({\mathsf O}_{身長} ,
S_{ [{}{\omega_J}]}{})
\\
{\mathsf M}_{{L^\infty (\Omega)}} ({\mathsf O}_{身長} ,
S_{ [{}{\omega_A}]}{})
\end{array}\right]
$
により得られた
測定値が
区間$[\alpha, \beta)$に属する確率は,
$
\qquad
\qquad
\left[\begin{array}{ll}
{}_{{{C_0(\Omega) }^*}} \Big( \delta_{\omega_J} , F_{身長}([\alpha, \beta) ) \Big){}_{L^\infty
(\omega, \nu )}
=
[F_{身長}([\alpha, \beta) )](\omega_J)
\\
{}_{{{C_0(\Omega) }^*}} \Big( \delta_{\omega_A} , F_{身長}([\alpha, \beta) ) \Big){}_{L^\infty
(\omega, \nu )}
=
[F_{身長}([\alpha, \beta) )](\omega_A)
\end{array}\right]
$
となる.
5.1.2: 正規観測量とスチューデントの$t$-分布
さて,
を考える.
$(C):$
ある粒子の位置$\omega$
$(\in {\mathbb R})$を,
誤差が標準偏差$\sigma$の正規分布
となる近似測定を行なうこと
\begin{align}
[G_{\sigma}(\Xi) ]( {\omega} {}) =
\frac{1}{{\sqrt{2 \pi } \sigma}}
\int_{\Xi} \exp
\left[
{}- \frac{1}{2 \sigma^2 } ({x} - {\omega} {})^2
\right] d{x}
\tag{5.1}
\\
\quad
(\forall \Xi \in {\cal B}_{{X}}^{}( ={\cal B}_{{\mathbb R}}^{}),
\;
\forall {\omega} \in \Omega (={\mathbb R} ){})
\nonumber
\end{align}
\begin{align}
&
[({{{\times}}}_{k=1}^n {G_\sigma})(\Xi_1 \times \Xi_2 \times
\cdots \times \Xi_n )](\omega)
=
{{{\times}}}_{k=1}^n [G_{\sigma}(\Xi_k) ]( {\omega} {})
\nonumber
\\
=
&
{{{\times}}}_{k=1}^n
\frac{1}{{\sqrt{2 \pi } \sigma}}
\int_{\Xi_k} \exp
\left[
{}- \frac{1}{2 \sigma^2 } ({x_k} - {\omega} {})^2
\right] d{x_k}
\quad
(\forall \Xi_k \in {\cal B}_{{X}}^{}( ={\cal B}_{{\mathbb R}}^{}),
\;
\forall {\omega} \in \Omega (={\mathbb R} ){})
\tag{5.3}
\end{align}

$(\sharp_1):$
なんでも大雑把に正規分布を仮定する
$(\sharp_2):$
一旦正規分布と仮定したら、それからは(スチューデントの$t$-観測量のような)詳細な解析を行う。
著者は、理論家より応用家を信用している。「大雑把+大雑把」または「詳細+詳細」ならわかる。 しかし、 その応用家が「雑な$(\sharp_1)$と詳細な$(\sharp_2)$」を現場で長年行っているのだとしたら、 それなりの必然性があるのだろうが、不思議な気がしないでもない。
