フィッシャーの最尤法と比べて、
特に、本質的というわけでないが、
モーメント法
も述べておこう。
下記の例5.13を見ればわかると思うが、
計算法としては、モーメント法は非常に優れている。
測定${\mathsf M}_{\cal A} \bigl({}{\mathsf O} \equiv
(X,{\mathcal F}, F) ,$
$ S_{[\rho] } \bigl)$の
$n$回の
並行測定
$\otimes_{k=1}^n
{\mathsf M}_{\cal A} \bigl({}{\mathsf O} \equiv
(X,{\mathcal F}, F) ,$
$ S_{[\rho] } \bigl)$
(=
${\mathsf M}_{\otimes {\cal A}} \big({} \bigotimes_{k=1}^n {\mathsf O}
:=
(
X^n,{\mathcal F}^n, \bigotimes_{k=1}^n F
) ,
S_{ [{}\otimes_{k=1}^n \rho{}]}{}\big)$
の測定値が,
$(x_1,$
$ x_2 ,$
$ ...,$
$ x_n ) (\in X^n)$
だったとしよう.
$n$は十分大きいとして, 大数の法則から,
\begin{align}
{\mathcal M_{+1}(X)} \ni
\nu_n
\Big(
\equiv
\frac{\delta_{x_1}+\delta_{x_2}+ \cdots + \delta_{x_n}}{n}
\Big)
≒\rho ( F (\cdot ))
\in
{\mathcal M_{+1}(X)}
\tag{5.18}
\end{align}
と考えてよいだろう.
それならば, 状態$\rho (\in {\frak S}^p({\mathcal A}^*))$を未知として,
測定
${\mathsf M}_{{L^\infty (\Omega) }} ({\mathsf O} {{=}}$
$
( \{ 白,$
$ 黒 \},$
$ 2^{\{ 白, 黒 \} } ,$
$ F{})
,
S_{ [{}{\ast}]}{})$
を考える.ここで,
$L^\infty(\Omega{})$内の観測量
${\mathsf O}_{白黒} = ( \{ 白, 黒 \}, 2^{\{ 白, 黒 \} } , F_{白黒}{})$
を次のように定義する:
\begin{align*}
& [F_{白黒}(\{ 白 \}{})](\omega_1{})= 0.8, & \quad & [
F_{白黒}(\{ 黒 \}{})](\omega_1{})= 0.2
\nonumber
\\
& [F_{白黒}(\{ 白 \}{})](\omega_2{})= 0.4, & \quad & [F_{白黒}(\{ 黒 \}{})]
(\omega_2{})= 0.6
\end{align*}
測定値「白」を得たのだから, 近似サンプル空間$( \{ 白, 黒 \}, 2^{\{ 白, 黒 \} } , \nu_1{})$は
\begin{align*}
\nu_1(\{ 白 \})=1,
\quad
\nu_1(\{黒 \})=0
\end{align*}
となる.
同時測定
${\mathsf M}_{{L^\infty (\Omega) }} (\times_{k=1}^{7}{\mathsf O} {{=}}$
$
( \{ 白,$
$ 黒 \}^7,$
$ 2^{{\{ 白, 黒 \} }^7} ,$
$\times_{k=1}^{7} F{})
,
S_{ [{}{\ast}]}{})$
の測定値が, (白, 黒, 黒, 白, 黒, 白, 黒
)と考えて, 「フィッシャーの最尤法」を使ってもよいが,
ここでは, モーメント法で解答しよう.
状態空間$\Omega (\approx {\frak S}^p(C_0(\Omega)^*))$
を
$\Omega={\mathbb R} \times {\mathbb R}_+$
$=\{ \omega =(\mu , \sigma ) \; |\; \mu \in {\mathbb R}, \sigma >0 \}$
として,
$L^\infty ({\Omega}{})$
内の
観測量
${\mathsf O}_{G} $
${{=}}$
$(X(={}{\mathbb R}) , {\cal B}_{{\mathbb R}}^{} ,
G{})$は
次を満たすとする
はずである.
$(A):$
左辺(=測定値$x_1, x_2,..., x_n )$)と観測量${\mathsf O} \equiv
(X,{\mathcal F}, F)$はわかっているのだから,
\begin{align*}
\mbox{未知状態$\rho (\in {\frak S}^p({\mathcal A}^*))$は
求めることができる}
\end{align*}
方程式(5.18)を解けばよいわけで、たとえば、以下のように様々な近似解を得る方法がある。

このような方法をモーメント法と呼ぶ.
$(B_1):$ 単純に考えるならば、次を解けば
よい。
\begin{align}
\| \nu_n(\cdot ) - \rho(F(\cdot ))\|_{{\mathcal M}(X)}
=
\min
\{
\| \nu_n(\cdot ) - \rho_1(F(\cdot ))\|_{{\mathcal M}(X)}
\;|
\;
\rho_1 (\in {\frak S}^p({\mathcal A}^*))
\}
\tag{5.19}
\end{align}
$(B_2):$
適当な$f_1, f_2, \cdots , f_n$
$\in C(X)$
$(=
X
\mbox{上の連続関数全体}
)$を最初に決めておいて,
並行測定
$\otimes_{k=1}^n{\mathsf M}_{\cal A} \bigl({}{\mathsf O} \equiv
(X,{\mathcal F}, F) ,$
$ S_{[\rho] } \bigl)$
の測定値が,
$(x_1, x_2 , ..., x_n ) (\in X)$
のとき,
\begin{align*}
&
\sum_{k=1}^n
\Big|
\int_X f_k(\xi) \nu_n (d \xi )
-
\int_X f_k(\xi) \rho( F(d \xi ))
\Big|
\\
=
&
\sum_{k=1}^n
\Big|
\frac{f_k({x_1})+f_k({x_2})+ \cdots + f_k({x_n})}{n}
-
\int_X f_k(\xi) \rho( F(d \xi ))
\Big|
\end{align*}
を最小にする$\rho (\in {\frak S}^p({\mathcal A}^*))$
を求めれば良い.
$(B_3):$
また,
古典測定
${\mathsf M}_{L^\infty (\Omega)} \bigl({}{\mathsf O} \equiv
(X,{\mathcal F}, F) ,$
$ S_{[*] } \bigl)$ならば,
未知状態は
$\rho=\delta_{\omega}$
と点測度で書けて,
\begin{align}
0=
\sum_{k=1}^n
\Big|
\frac{f_k({x_1})+f_k({x_2})+ \cdots + f_k({x_n})}{n}
-
\int_X f_k(\xi) [F(d \xi )](\omega)
\Big|
\tag{5.20}
\end{align}
を解く方法は有効で, すなわち,未知数$\omega (\in \Omega)$の
連立方程式:
\begin{align*}
\begin{cases}
\frac{f_1({x_1})+f_1({x_2})+ \cdots + f_1({x_n})}{n}
-
\int_X f_1(\xi) [F(d \xi )](\omega)=0
\\
\\
\frac{f_2({x_1})+f_2({x_2})+ \cdots + f_2({x_n})}{n}
-
\int_X f_2(\xi) [F(d \xi )](\omega)=0
\\
\qquad \dots \dots
\\
\qquad \dots \dots
\\
\frac{f_m({x_1})+f_m({x_2})+ \cdots + f_m({x_n})}{n}
-
\int_X f_m(\xi) [F(d \xi )](\omega)=0
\end{cases}
\end{align*}
を解く方法は,有効なことが多い.
$(B_4):$
特に,
$X=\{\xi_1, \xi_2, \cdots , \xi_m \}$が有限集合ならば,
$f_1, f_2, \cdots , f_m$
$\in C(X)$を
\begin{align*}
f_k(\xi) = \chi_{{}_{\{\xi_k \}}}(\xi)=\begin{cases}
1 \quad & (\xi= \xi_k)
\\
0 & ( \xi \not=\xi_k )
\end{cases}
\end{align*}
と決めておいて,
並行測定
$\otimes_{k=1}^n{\mathsf M}_{\cal A} \bigl({}{\mathsf O} \equiv
(X,{\mathcal F}, F) ,$
$ S_{[*] } \bigl)$
の測定値が,
$(x_1, x_2 , ..., x_n ) (\in X)$
のとき,
\begin{align*}
&
\sum_{k=1}^n
\Big|
\frac{
\chi_{{}_{\{\xi_k \}}}({x_1})+ \chi_{{}_{\{\xi_k \}}}({x_2})+ \cdots +\chi_{{}_{\{\xi_k \}}} ({x_n})}{n}
-
\int_X \chi_{{}_{\{\xi_k \}}}( \xi) \rho( F(d \xi ))
\Big|
\\
=
&
\sum_{k=1}^n
\Big|
\frac{\sharp[\{x_m \;:\; \xi_k=x_m \}]}{n}
-
\rho( F( \{ \xi_k\} ))
\Big|
\end{align*}
を最小にする$\rho (\in {\frak S}^p({\mathcal A}^*))$
を求めれば良い
注意点は,
$(C_1):$
もちろん, (気分は大数の法則なのだから)$n$が十分に大きいことが好ましいが, 極端な話,
$n=1$でも「それなりの推定」になる
$(C_2):$
($B_2$)のように,
$f_k$の選び方は人為的だが,使いやすい.
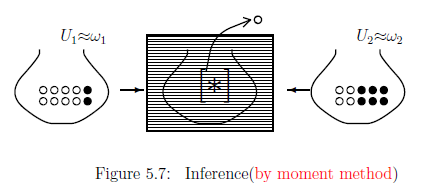
カーテンの後ろの壷から球を一つ取り出したら,白球だった.
このとき,壷は$U_1$または$U_2$のどちらか?$\;\;$これを推定せよ.
[未知状態
$[\ast]$
が$\omega_1$のとき]
\begin{align*}
(5.19)=|1-0.8|+|0-0.2|=0.4
\end{align*}
[未知状態
$[\ast]$が
$\omega_2$のとき]
\begin{align*}
(5.19)=|1-0.4|+|0-0.6|=1.2
\end{align*}
よって,モーメント法($B_1$)により,
状態$\omega_1$が推定できて,
したがって,
カーテンの後ろの壷は$U_1$
であることが推定できる.
簡単すぎて, 大数の法則が見えなくなっていて, 却って難しくなってしまったかもしれないので, もう一つ次の問題を補足しておく.
である.
$(a):$
カーテンの後ろの壷は, どちらの壷か?
[未知状態
$[\ast]$
が$\omega_1$のとき]
\begin{align*}
(5.19)
=|3/7-0.8|+|4/7-0.2|=52/70
\end{align*}
[未知状態
$[\ast]$が
$\omega_2$のとき]
\begin{align*}
(5.19)
=|3/7-0.4|+|4/7-0.6|=10/70
\end{align*}
よって,($B_1$)により,
状態$\omega_2$が推定できて,
したがって,
カーテンの後ろの壷は$U_2$
であることが推定できる.
例 5.13 [頻出するモーメント法]
\begin{align*}
&
\int_{\mathbb R} \xi [G( d \xi )](\mu, \sigma )=\mu, \quad
\int_{\mathbb R} (\xi -\mu)^2 [G( d \xi )](\mu, \sigma )=\sigma^2
\\
&
\quad
\qquad
(
\forall {\omega}=(\mu, \sigma) \in \Omega (={\mathbb R} \times {\mathbb R}_+ ){})
\end{align*}
ここに,${\cal B}_{\mathbb R}$はボレル集合体
とする.
このとき,
同時測定
${{{\times}}}_{k=1}^3{\mathsf M}_{L^\infty(\Omega )} ({\mathsf O}_{G}, S_{[{}\ast{}] }{})$
によって,$(x_1, x_2, x_3 ) (\in {\mathbb R}^3)$が得られたとしよう.
したがって,3標本分布$\nu_3$は
\begin{align*}
\nu_3 = \frac{
\delta_{x_1}+\delta_{x_2}+\delta_{x_3}}{3}
\in {\mathcal M}_{+1}({\mathbb R})
\end{align*}
となる.
$$f_1(\xi)=\xi, \quad f_2(\xi)=\xi^2$$
としよう.
モーメント法($B_3$)より,
\begin{align*}
0=&
\sum_{k=1}^2
\Big|
\int_{\mathbb R} \xi^k \nu_3 (d \xi )
-
\int_{\mathbb R} \xi^k [G(d \xi )](\omega)
\Big|
\\
=
&
\sum_{k=1}^2
\Big|
\frac{({x_1})^k+({x_2})^k+ ({x_n})^k}{3}
-
\int_{\mathbb R} \xi^k [G(d \xi )](\mu, \sigma)
\Big|
\\
=
&
\Big|
\frac{{x_1}+{x_2}+ {x_3}}{3}
-
\mu
\Big|
+
\Big|
\frac{({x_1})^2+({x_2})^2+ ({x_3})^2}{3}
-
(\sigma^2 + \mu^2
)
\Big|
\end{align*}
よって,
\begin{align*}
\mu &=\frac{{x_1}+{x_2}+ {x_n}}{3}
\\
\sigma^2 &
=
\frac{({x_1})^2+({x_2})^2+ ({x_3})^2}{3}
-\mu^2
\\
&
=
\frac{({x_1}- \frac{{x_1}+{x_2}+ {x_n}}{3} )^2+({x_2}- \frac{{x_1}+{x_2}+ {x_n}}{3} )^2+ ({x_3} - \frac{{x_1}+{x_2}+ {x_n}}{3} )^2}{3}
\end{align*}
となる.正規分布を仮定していないにもかかわらず、これは,式(5.13)と同じであることに注意せよ.
$\fbox{注釈5.3}$
測定${\mathsf M}_{\overline{\mathcal A}}({\mathsf O} {{=}} (X,2^X, F),$
$ S_{[\ast]} )$
を考える. ただし, $X=\{x_1,x_2,...,x_n\}$は有限集合とする. このとき
「フィッシャーの最尤法」とモーメント法」は, 同じ結論を推定することを確かめよ.
[解答]
測定${\mathsf M}_{\overline{\mathcal A}}({\mathsf O} {{=}} (X,2^X, F),$
$ S_{[\ast]} )$によって, 測定値$x_m (\in X)$が得られたとしよう.
[フィッシャーの最尤法]:
[モーメント法]:
$(a):$
$\rho ( F(\{ x_m\})$を最大にする$\rho ( \in {\frak S}^p({\mathcal A}^*))$求めよ.
よって, 「フィッシャーの最尤法」とモーメント法」は, 同じ結論を導く。
$(b):$
近似サンプル空間は, $(X, 2^X, \delta_{x_m} )$となるので,
\begin{align*}
&
|0- \rho ( F(\{ x_1 \})|+ \cdots +|0- \rho ( F(\{ x_{m-1}\})|+
|1- \rho ( F(\{ x_{m}\})|
\\
&
\qquad
+|0- \rho ( F(\{ x_{m+1}\})|+\cdots +|0- \rho ( F(\{ x_{n}\})|
\\
=
&
\rho ( F(\{ x_1 \})+ \cdots +\rho ( F(\{ x_{m-1}\})+
(1- \rho ( F(\{ x_{m}\}))
\\
&
\qquad
+\rho ( F(\{ x_{m+1}\})+\cdots +\rho ( F(\{ x_{n}\})
\\
=
&
1- 2\rho ( F(\{ x_{m}\})
\end{align*}
を最小にする$\rho ( \in {\frak S}^p({\mathcal A}^*))$を求めよ.
5.4:モーメント法 (人為的だが役に立つ)
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
問題5.11 [=壺問題:モーメント法の演習問題:壺問題5.2の再掲 ]
どちらの壷($U_1$ または $U_2$)がカーテンの後ろに
置かれているのかあなたは知らない.
[壺問題5.2のモーメント法による解答]
問題5.12 [復元抽出]:
上述のように, 「白」を取り出しとしよう. この「白球」を壷に戻してよくかき混ぜて, 次に取り出したのが「黒」だとしよう. これを全部で7回行って,
結局
\begin{align*}
白, 黒, 黒, 白, 黒, 白, 黒,
\end{align*}
を得たとしよう. そこで問題:
解答:
