本書では、「モンティホール問題」について何度か議論する (cf. $\S$5,5, $\S$9.6, $\S$9.7, $\S$9.9, $\S$18.2). チョット間違いやすいクイズだから、モンティホール問題を何度も議論するわけではない。

  • モンティホール問題は二元論の本質を浮き彫りにする問題
だから、何度も議論するのである。
この節は、次からの抜粋である。
$(\sharp):$ S. Ishikawa, "Monty Hall Problem and the Principle of Equal Probability in Measurement Theory," Applied Mathematics , Vol. 3, No. 7, 2012, pp. 788-794. doi:10.4236/am.2012.37117 ( download free)

問題5.14 [モンティホール問題(フィッシャーの最尤法による解答)] あなたはゲームショーに出演している． 3つのドア (すなわち，「1番」， 「2番」， 「3番」 ) のうちの 1つのドアの後ろには自動車(当り), 他の2つのドアの後ろには 羊(はずれ)が隠されている． 司会者は，どのドアの後ろに自動車が隠されているかを知っている． しかし，あなたはそれを知らない．

ここで, 司会者は問う：「どのドアの後ろが自動車だと思いますか？」

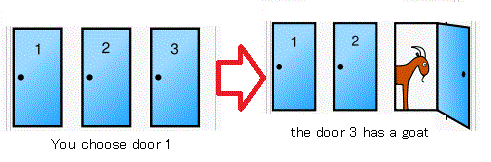
さて，あなたはあるドアを選んだと仮定する． たとえば, 1番のドアを選んだとする． このとき， 司会者が 「実は，3番ドアの後ろは羊です」 と言う． 更に，司会者は問う． 「あなたは1番のドアを選んでしまいましたが， 今からでも変更可能ですよ． 2番のドア に変更しますか？ 」と． さて，あなたはどうするか？
解答:

状態空間を$\Omega = \{ \omega_1 , \omega_2 , \omega_3 \}$(離散距離空間)とおく． ここに，



\begin{align*} \omega_1 & \cdots \cdots \text{ 1番ドアの後ろに自動車が隠れている状態} \\ \omega_2 & \cdots \cdots \text{ 2番ドアの後ろに自動車が隠れている状態} \\ \omega_3 & \cdots \cdots \text{ 3番ドアの後ろに自動車が隠れている状態} \end{align*}

として, \begin{align*} \mbox{ 古典基本構造$[ C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]\qquad$ (ここに, $ \nu(\{\omega_k \})=1, \; k=1,2,3$) } \end{align*} を得る.

また， $L^\infty(\Omega)$内の 観測量 ${\mathsf O}$ ${{=}}$ $(\{ 1, 2,3 \}, 2^{\{1, 2 ,3\}}, F)$ は 次のように定義される．

\begin{align} & [F(\{ 1 \}{})](\omega_1{})= 0.0,\qquad [F(\{ 2 \}{})](\omega_1{})= 0.5, \qquad [F(\{ 3 \}{})](\omega_1{})= 0.5 \nonumber \\ & [F(\{ 1 \}{})](\omega_2{})= 0.0,\qquad [F(\{ 2 \}{})](\omega_2{})= 0.0, \qquad [F(\{ 3 \}{})](\omega_2{})= 1.0 \nonumber \\ & [F(\{ 1 \}{})](\omega_3{})= 0.0,\qquad [F(\{ 2 \}{})](\omega_3{})= 1.0, \qquad [F(\{ 3 \}{})](\omega_3{})= 0.0 \tag{5.21} \end{align}

したがって, あなたは測定 ${\mathsf M}_{L^\infty(\Omega)} ({\mathsf O} {{=}} (\{ 1, 2,3 \}, 2^{\{1, 2 ,3\}}, F), S_{[{}\ast{}]})$ ─ 「1番ドアの後ろに自動車が隠れている」 と言って， 司会者の返事を聞く測定 ─ を行ったことになる．

\begin{align*} (1)\ & \text{測定値 $1$ を得る} \Longleftrightarrow \text{司会者が「1番ドアの後ろに 羊がいる」と言う} \\ (2)\ & \text{測定値 $2$ を得る} \Longleftrightarrow \text{司会者が「2番ドアの後ろに 羊がいる」と言う} \\ (3)\ & \text{測定値 $3$ を得る} \Longleftrightarrow \text{司会者が「3番ドアの後ろに 羊がいる」と言う} \end{align*} とする．

司会者が「3番ドアの後ろに 羊がいる」と教えてくれたのだから， 測定 ${\mathsf M}_{L^\infty(\Omega)} ({\mathsf O},$ $ S_{[\ast]}{})$ によって， 測定値" 3"を得たことになる． したがって, フィッシャーの最尤法(定理5.6)により， あなたは 2番ドアを選ぶべきだ となる．なぜならば

\begin{align*} \max \{ [F(\{3\}{})] (\omega_1{}), [F(\{3 \}{}){}](\omega_2{}), [F(\{3 \}{})] (\omega_3{}) \} & =\max \{ 0.5, \; \; 1.0 , \; \; 0.0 \} \\ & = 1.0 = [F(\{3\}{})] (\omega_2{}) \end{align*}

なので， $[\ast]$ $=$ ${\omega_2}$ と推定できる． したがって，あなたは 2番ドアに変更すべきである．

$\fbox{注釈5.4}$上記の解答を見れば，問い掛け「測定とは，何か？」 が，無理難題で， 広辞苑的定義以上のものを期待できないことが， わかると思う(注釈2.5参照)． すなわち、
  • 「測定」は形而上学的概念である
とか
  • 「測定」という言葉は、言語ルール1の言葉遣いで使うしかない
ことを了解してもらえると思う。。
上の解答は，モンティ・ホール問題の正式な解答の1つである． モンティ・ホール問題の解答は， (統計学の)ベイズの定理 を使った解答が普通で， これは第9章「ベイズ統計」と 第18章「信念の確率」 で述べる.

注意5.15 [モンティホール問題(モーメント法による解答)] (5.4節の注釈5.3の議論「フィッシャーの最尤法=モーメント法」を使えば、以下の計算は不要)

あなたは測定 ${\mathsf M}_{L^\infty (\Omega )} ({\mathsf O} {{=}} (\{ 1, 2,3 \}, 2^{\{1, 2 ,3\}}, F),$ $ S_{[{}\ast{}]})$ ─ 「1番ドアの後ろに自動車が隠れている」 と言って， 司会者の返事を聞く測定 ─ を行ったことになる． 測定値「3」を得たのだから, 近似サンプル空間 $(\{1,2,3\}, 2^{\{1,2,3\}}, \nu_{1}{})$ を得た.　すなわち, $\nu_1 ({}\{1 \}{}) =0 $, $\nu_1 ({}\{2 \}{}) =0 $, $\nu_1 ({}\{3 \}{}) =1 $ を得た. したがって,

[未知状態 $[\ast]$ が$\omega_1$のとき] \begin{align*} (5.19)=|0-0|+ | 0 - 0.5| + | 1- 0.5| = 1, \end{align*}

[未知状態 $[\ast]$が $\omega_2$のとき] \begin{align*} (5.19)=|0-0|+ | 0 - 0| + | 1-1| = 0 \end{align*}

[未知状態 $[\ast]$が $\omega_3$のとき] \begin{align*} 式(5.19)=|0-0|+ | 0 - 1| + | 1-0| = 2. \end{align*} なので， モーメント法によって、 $[\ast]$ $=$ ${\omega_2}$ と推定できる． したがって，あなたは 2番ドアに変更すべきである．