6.4.3: 仮説検定[帰無仮説$H_N=\{\sigma_0\} \subseteq \Theta = {\mathbb R}_+$]



問題： $x_1, x_2, .... x_n $を正規分布$N(\mu, \sigma )$ (母平均$\mu$は既知、母分散$\sigma$は未知)から得られたデータとする。 $ {\overline \mu} (x)= \frac{x_1 + x_2 + ...+ x_n }{n} $, $ {\overline \sigma} (x)= \Big( \frac{(x_1 - {\overline \mu}(x) )^2 + (x_2- {\overline \mu}(x) )^2 + ...+ (x_n- {\overline \mu}(x))^2 }{n}\Big)^{1/2} $ とする。
このとき、我々の問題は

  • $ \sigma = \sigma_0 $ と仮定したとき、 「$ \sigma_0 e^{\eta } \le {\overline \sigma} (x) $ または ${\overline \sigma} (x) \le \sigma_0 e^{- \eta}$ 」ということは滅多におこらないような、最小の$\eta (> 0)$を求めよ。

である。

この問題を量子言語に翻訳すると、以下のようになる。
問題6.13 [仮説検定]. 同時正規測定 ${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$ $({\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$ $S_{[(\mu, \sigma)]})$ を考えよう.ここで, \begin{align*} \sigma = \sigma_0 \end{align*} と仮定しよう.すなわち,帰無仮説を$H_N=\{ \sigma_0 \}$ $(\subseteq \Theta= {\mathbb R} ) )$ と仮定する.$0 < \alpha \ll 1$とする. このとき,次を満たす${\widehat R}_{{H_N}}^{\alpha; \Theta}( \subseteq \Theta)$で,「出来るだけ大きいもの($\mu$に依存してもよい)」を見つけよ
$\bullet$ ${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$ $({\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$ $S_{[(\mu_0, \sigma)]})$の測定値$x(\in{\mathbb R}^n )$が, \begin{align*} E(x) \in {\widehat R}_{{H_N}}^{\alpha; \Theta} \end{align*} を満たす確率は,$\alpha$以下である.

もちろん、棄却域 ${\widehat R}_{{H_N}}^{\alpha; \Theta}$は大きければ大きいほどよい。

解答

半距離$d_{\Theta}^{(1)}$は(6.46)で定めた. 各 $ \omega=(\mu, {\sigma} ) ({}\in \Omega= {\mathbb R} \times {\mathbb R}_+ )$ に対して, 正数 $\eta^{\alpha}_{\omega}$ $({}> 0)$ を以下のように定める： \begin{align} \eta^{\alpha}_{\omega} & = \inf \{ \eta > 0: [F ({}E^{-1} ({} {{\rm Ball}^C_{d_{\Theta}^{(1)}}}(\omega ; \eta{}))](\omega ) \le \alpha \} \nonumber \end{align} また、次を思い出そう。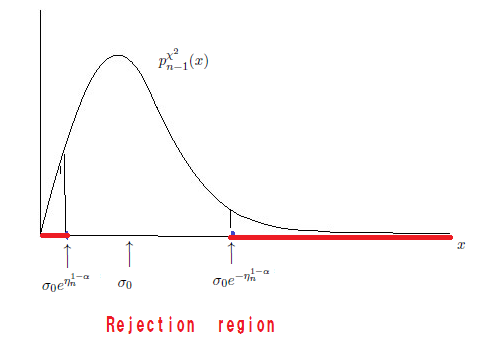 \begin{align*} \eta_\omega^\alpha = \delta_\omega^{1-\alpha} = \delta_n^{1-\alpha} (= \eta_n^\alpha ) \end{align*} 式(6.20)により, ${\widehat R}_{H_N}^{\alpha, \Theta}$ ( $({}\alpha{})$-棄却域； 帰無仮説 $H_N= \{ \sigma_0 \} \subseteq \Theta ={\mathbb R}_+$ ) は以下のようになる： \begin{align} {\widehat R}_{H_N}^{\alpha, \Theta} & = {\widehat R}_{\{ \sigma_0 \}}^{\alpha, \Theta} = \bigcap_{\pi(\omega ) = \sigma \in \{\sigma_0 \}} \{ {E(x)} (\in \Theta) : d^{(1)}_\Theta ({}E(x), \omega) \ge \eta^\alpha_{\omega} \} \nonumber \\ & = \{ {E(x)} (\in \Theta={\mathbb R}_+) : d^{(1)}_\Theta ({}E(x), (\mu, \sigma_0)) \ge \eta^\alpha_{n} \} \nonumber \\ & = \{ \overline{\sigma}(x) (\in \Theta ={\mathbb R}_+ ) \;: \; \overline{\sigma}(x) \le {\sigma_0} e^{ -\eta^\alpha_{n} } \mbox{ or } {\sigma_0} e^{\eta^\alpha_{n} } \le \overline{\sigma}(x) \} \tag{6.55} \end{align} ここに, $\overline{\sigma}(x) = \Big( \frac{\sum_{k=1}^n ( x_k - \overline{\mu} (x))^2}{n} \Big)^{1/2} $. 注意6.10と同じ意味で, \begin{align} & {\widehat R}_{{\mathbb R} \times \{\sigma_0 \}}^{\alpha} = \{ (\mu , \overline{\sigma}(x) ) \in {\mathbb R} \times {\mathbb R}_+ \;:\; \overline{\sigma}(x) \le {\sigma_0} e^{ -\eta^\alpha_{n} } \mbox{ or } {\sigma_0} e^{\eta^\alpha_{n} } \le \overline{\sigma}(x) \} \\ & \tag{6.56} \end{align}

6.4.4: 仮説検定[帰無仮説$H_N=(0, \sigma_0] \subseteq \Theta = {\mathbb R}_+$]


問題： $x_1, x_2, .... x_n $を正規分布$N(\mu, \sigma )$ (母平均$\mu$は既知、母分散$\sigma$は未知)から得られたデータとする。 $ {\overline \mu} (x)= \frac{x_1 + x_2 + ...+ x_n }{n} $, $ {\overline \sigma} (x)= \Big( \frac{(x_1 - {\overline \mu}(x) )^2 + (x_2- {\overline \mu}(x) )^2 + ...+ (x_n- {\overline \mu}(x))^2 }{n}\Big)^{1/2} $ とする。
このとき、我々の問題は

  • $ \sigma \le \sigma_0 $ と仮定したとき、 「$ \sigma_0 e^{\eta } \le {\overline \sigma} (x) $ 」ということは滅多におこらないような、最小の$\eta (> 0)$を求めよ。

である。

この問題を量子言語に翻訳すると、以下のようになる。

問題6.14 [仮説検定].

同時正規測定 ${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$ $({\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$ $S_{[(\mu, \sigma)]})$ を考えよう.ここで, \begin{align*} \sigma \in (0, \sigma_0] \end{align*} と仮定しよう.すなわち,帰無仮説を$H_N=(0, \sigma_0]$ $(\subseteq \Theta= {\mathbb R} ) )$ と仮定する.$0 < \alpha \ll 1$とする. このとき,次を満たす${\widehat R}_{{H_N}}^{\alpha; \Theta}( \subseteq \Theta)$で,「出来るだけ大きいもの($\mu$に依存してもよい)」を見つけよ

$\bullet$ ${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$ $({\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$ $S_{[(\mu_0, \sigma)]})$の測定値$x(\in{\mathbb R}^n )$が, \begin{align*} E(x) \in {\widehat R}_{{H_N}}^{\alpha; \Theta} \end{align*} を満たす確率は,$\alpha$以下である.

解答

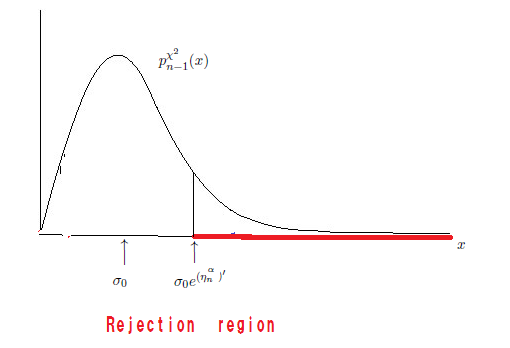
$\Theta (={\mathbb R}_+ )$内に 次の半距離 $d_{\Theta}^{(2)}$ を考える.

\begin{align} d_{\Theta}^{(2)}(\sigma_1,\sigma_2) = \left\{\begin{array}{ll} | \int_{\sigma_1}^{\sigma_2} \frac{1}{\sigma} d \sigma | = |\log{\sigma_1} - \log{\sigma_2}| \quad & ( \sigma_0 \le \sigma_1, \sigma_2 ) \\ | \int_{\sigma_0}^{\sigma_2} \frac{1}{\sigma} d \sigma | = |\log{\sigma_0} - \log{\sigma_2}| \quad & ( \sigma_1 \le \sigma_0 \le \sigma_2 ) \\ | \int_{\sigma_0}^{\sigma_1} \frac{1}{\sigma} d \sigma | = |\log{\sigma_0} - \log{\sigma_1}| \quad & ( \sigma_2 \le \sigma_0 \le \sigma_1 ) \\ 0 \quad & ( \sigma_1, \sigma_2 \le \sigma_0 ) \end{array}\right. \tag{6.57} \end{align}

任意の $ \omega=(\mu, {\sigma} ) ({}\in \Omega= {\mathbb R} \times {\mathbb R}_+ )$に対して, 正数 $\eta^\alpha_{\omega}$ $({}> 0)$ を次のように定める. \begin{align} \eta^\alpha_{\omega} = \sup \{ \eta > 0: [G ^n ({}E^{-1} ({} {{\rm Ball}^c_{d_{\Theta}^{(2)}}}(\pi(\omega) ; \eta{}))](\omega ) \le \alpha \} \tag{6.58} \end{align} ここで, $\pi(\omega ) = \sigma \in H_N = (0 , \sigma_0 ] $とする. \begin{align} & {{\rm Ball}^c_{d_{\Theta}^{(2)}}}(\pi(\omega) ; \eta ) = {{\rm Ball}^c_{d_{\Theta}^{(2)}}}( {\sigma} , \eta ) = \{ \sigma' \;:\; \log(\sigma'/{\sigma_0}) \ge \eta \} \nonumber \\ \subseteq & \{ \sigma' \;:\; \log(\sigma'/{\sigma}) \ge \eta \} = [{\sigma} e^{\eta} , \infty ) \tag{6.59} \end{align} したがって, \begin{align} & E^{-1}( { {\rm Ball}^c_{d_{\Theta}^{(1)}} } (\pi (\omega ); \eta )) \subseteq E^{-1} \Big( [{\sigma} e^{\eta} , \infty ) \Big) \nonumber \\ = & \Big\{ (x_1, \ldots , x_n ) \in {\mathbb R}^n \;: \; {\sigma} e^{ \eta } \le \Big( \frac{\sum_{k=1}^n ( x_k - \overline{\mu} (x))^2}{n} \Big)^{1/2} \Big\} \tag{6.60} \end{align} よって,自由度$(n-1)$の$\chi^2$-分布の確率密度関数$p^{{\chi}^2}_{n-1}({ x} )$を用いて,ガウス積分の公式(6.7)から次を得る.

  • (ガウス積分の公式(6.7)の導出は意外と難しい)
\begin{align} & [{{{G}}}^n (E^{-1}({{\rm Ball}^c_{d_{\Theta}^{(1)}}}(\omega; \eta ))] ({}\omega{}) \nonumber \\ \le & \frac{1}{({{\sqrt{2 \pi }{\sigma}{}}})^n} \underset{{ E^{-1} \Big( [{\sigma} e^{\eta} , \infty ) \Big) }}{\int \cdots \int} \exp[{}- \frac{\sum_{k=1}^n ({}{}{x_k} - {}{\mu} {})^2 } {2 {\sigma}^2} {}] d {}{x_1} d {}{x_2}\cdots dx_n \nonumber \\ = & \int_{{n} e^{ 2 \eta}}^\infty p^{\chi^2}_{n-1} (x ) dx \tag{6.61} \end{align} 次式を解いて, $(\eta^\alpha_{n})' (>0)$ を得る。 \begin{align} \alpha = \int_{{n} e^{2 (\eta^\alpha_{n})'}}^{\infty} p^{\chi^2}_{n-1} (x ) dx \tag{6.62} \end{align}

したがって,$({}\alpha{})$-棄却域 ${\widehat R}_{H_N}^{\alpha}$ ( 帰無仮説 $H_N= (0, \sigma_0] $ ) は以下のようになる.

\begin{align} {\widehat R}_{H_N}^{\alpha, \Theta} & = \bigcap_{\pi(\omega ) = \omega \in (0, \sigma_0 ]} \{ {E(x)} (\in \Theta) : d^{(2)}_\Theta ({}E(x), \pi(\omega) ) \ge \eta^\alpha_{\omega} \} \nonumber \\ & = \{ {E(x)} (\in \Theta) : d^{(2)}_\Theta ({}E(x), \omega) \ge (\eta^\alpha_{n})' \} \nonumber \\ & = \{ \overline{\sigma}(x) \in {\mathbb R}_+ \;: \; {\sigma_0} e^{(\eta^\alpha_{n})' } \le \overline{\sigma}(x) \} \tag{6.63} \end{align}

ここで, $\overline{\sigma}(x) = \Big( \frac{\sum_{k=1}^n ( x_k - \overline{\mu} (x))^2}{n} \Big)^{1/2} $. 注意6.10と同じ意味で,

\begin{align} {\widehat R}_{{\mathbb R} \times (0, \sigma_0]}^{\alpha} = \{ (\mu , \overline{\sigma}(x) ) \in {\mathbb R} \times {\mathbb R}_+ \;:\; \;: \; {\sigma_0} e^{(\eta^\alpha_{n})' } \le \overline{\sigma}(x) \} \tag{6.64} \end{align}