$L^\infty({\mathbb R} \times {\mathbb R}_+)$内の
同時正規測定
${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$
$({\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$
$S_{[(\mu, \sigma)]})$を考えよう.
ここに,
$L^\infty({\mathbb R} \times {\mathbb R}_+)$内の
同時正規観測量
${\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n} )$
を以下のように定めたことを思い出そう.
6.4.2: 信頼区間
$\Theta (={\mathbb R}_+ )$内に
次の半距離 $d_{\Theta}^{(1)}$
を考える.
任意の
$ \omega=(\mu, {\sigma} ) ({}\in
\Omega=
{\mathbb R} \times {\mathbb R}_+ )$に対して,
正数
$\eta^\alpha_{\omega}$
$({}> 0)$
を次のように定める.
\begin{align}
\eta^\alpha_{\omega}
=
\sup
\{
\eta > 0:
[F ({}E^{-1} ({}
{{\rm Ball}^c_{d_{\Theta}^{(1)}}}(\pi(\omega) ; \eta{}))](\omega )
\le \alpha
\}
\tag{6.47}
\end{align}
ここで,
\begin{align}
&
{{\rm Ball}^c_{d_{\Theta}^{(1)}}}(\pi(\omega) ; \eta )
=
{{\rm Ball}^c_{d_{\Theta}^{(1)}}}( {\sigma} , \eta )
=
\{ \sigma' \;:\; |\log(\sigma'/{\sigma})| \ge \eta
\}
\nonumber
\\
=
&
(0,{\sigma} e^{-\eta}] \cup [{\sigma} e^{\eta} , \infty )
\tag{6.48}
\end{align}
したがって,
\begin{align}
&
E^{-1}( {{\rm Ball}^c_{d_{\Theta}^{(1)}}}(\omega ; \eta ))
=
E^{-1}
\Big(
(0,{\sigma} e^{-\eta}] \cup [{\sigma} e^{\eta} , \infty )
\Big)
\nonumber
\\
=
&
\Big\{
(x_1, \ldots , x_n )
\in
{\mathbb R}^n
\;:
\;
\Big(
\frac{\sum_{k=1}^n ( x_k -
\overline{\mu}
(x))^2}{n}
\Big)^{1/2}
\le
{\sigma} e^{ -\eta }
\mbox{ or }
{\sigma} e^{ \eta }
\le
\Big(
\frac{\sum_{k=1}^n ( x_k -
\overline{\mu}
(x))^2}{n}
\Big)^{1/2}
\Big\}
\nonumber
\\
&
\tag{6.49}
\end{align}
よって,自由度$(n-1)$の$\chi^2$-分布の確率密度関数$p^{{\chi}^2}_{n-1}({ x} )$を用いて,ガウス積分の公式(6.7)から次を得る.
ここで,
$\eta^\alpha_{\omega}$は$\alpha$と$n$に依存するが,
$\omega$に依存しないことがわかる.
すなわち,
6.4(1): 母分散 (信頼区間法)
6.4.1: 準備 (同時正規測定)
\begin{align}
&
[{{{G}}}^n
({\mathop{\Large \mbox{$\times$}}}_{k=1}^n \Xi_k)]
({}\omega{})
=
{\mathop{\Large \mbox{$\times$}}}_{k=1}^n
[{{{G}}}(\Xi_k)](\omega)
\nonumber
\\
=
&
\frac{1}{({{\sqrt{2 \pi }\sigma{}}})^n}
\underset{{{\mathop{\Large \mbox{$\times$}}}_{k=1}^n \Xi_k }}{\int \cdots \int}
\exp[{}- \frac{\sum_{k=1}^n ({}{}{x_k} - {}{\mu} {})^2
}
{2 \sigma^2} {}] d {}{x_1} d {}{x_2}\cdots dx_n
\tag{6.45}
\\
&
\qquad
({}\forall \Xi_k \in {\cal B}_{{\mathbb R}{}}^{}
({}k=1,2,\ldots, n),
\quad
\forall {}{\omega}=(\mu, \sigma ) \in \Omega = {\mathbb R}\times {\mathbb R}_+{}).
\nonumber
\end{align}
したがって,状態空間$\Omega$と測定値空間$X$は
\begin{align*}
&
\Omega = {\mathbb R} \times {\mathbb R}_+
\\
&
X={\mathbb R}^n
\end{align*}
となる. 第二状態空間$\Theta$は
\begin{align*}
&
\Theta = {\mathbb R}_+
\end{align*}
とする. ここで,
\begin{align*}
\overline{\mu}(x)
=
\frac{x_1 + x_2 + \cdots + x_n}{n}
\end{align*}
として,
推定量
$E: {\mathbb R}^n \to \Theta (\equiv {\mathbb R}_+ )$
を
\begin{align}
&
E(x)=E(x_1, x_2, \ldots , x_n )
=
\sqrt{
\frac{(x_1-\overline{\mu}(x))^2 + (x_2-\overline{\mu}(x))^2 + \cdots + (
x_n-\overline{\mu}(x))^2 }{n}
}
\end{align}
システム量$\pi: \Omega \to \Theta $を
\begin{align}
&
\Omega={\mathbb R} \times {\mathbb R}_+
\ni
\omega = (\mu, \sigma )
\mapsto \pi (\omega ) = \sigma \in \Theta={\mathbb R}_+
\end{align}
で定義する.
問題:
$x_1, x_2, .... x_n $を正規分布$N(\mu, \sigma )$
(母平均$\mu$は既知、母分散$\sigma$は未知)から得られたデータとする。
$
{\overline \mu} (x)= \frac{x_1 + x_2 + ...+ x_n }{n}
$,
$
{\overline \sigma} (x)= \Big( \frac{(x_1 - {\overline \mu}(x) )^2 + (x_2- {\overline \mu}(x) )^2 + ...+ (x_n- {\overline \mu}(x))^2 }{n}\Big)^{1/2}
$
とする。
このとき、我々の問題は
である。
この問題を量子言語に翻訳すると、以下のようになる。
$\bullet$
「$\sigma \in
{D}_{x}^{1- \alpha; \Theta}$」である確率が,$1-\alpha$以上である.
\begin{align}
&
[{{{G}}}^n
(E^{-1}({{\rm Ball}^c_{d_{\Theta}^{(1)}}}(\omega; \eta ))]
({}\omega{})
\nonumber
\\
=
&
\frac{1}{({{\sqrt{2 \pi }{\sigma}{}}})^n}
\underset{{
E^{-1}
\Big(
(0,{\sigma} e^{-\eta}] \cup [{\sigma} e^{\eta} , \infty )
\Big)
}}{\int \cdots \int}
\exp[{}- \frac{\sum_{k=1}^n ({}{}{x_k} - {}{\mu} {})^2
}
{2 {\sigma}^2} {}] d {}{x_1} d {}{x_2}\cdots dx_n
\nonumber
\\
=
&
\int_0^{{n} e^{- 2 \eta}}
p^{\chi^2}_{n-1} (x )
dx
+
\int_{{n} e^{ 2 \eta}}^\infty
p^{\chi^2}_{n-1} (x )
dx
=
1-
\int_{{n} e^{- 2 \eta}}^{{n} e^{ 2 \eta}}
p^{\chi^2}_{n-1} (x )
dx
\tag{6.50}
\end{align}
よって,
$\eta^\alpha_{\omega}$
が次のように定まる.
\begin{align}
1-
\alpha
=
\int_{{n} e^{-2 \eta^\alpha_{\omega}}}^{{n} e^{2 \eta^\alpha_{\omega}}}
p^{\chi^2}_{n-1} (x ) dx
\tag{6.51}
\end{align}

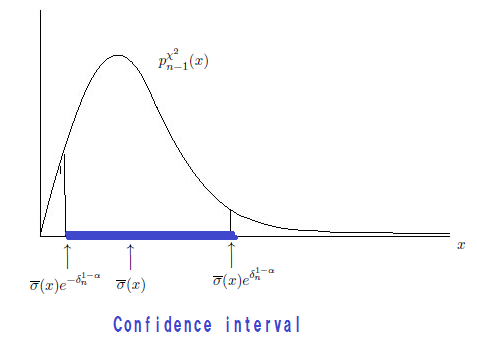
6.4(1): 母分散 (信頼区間と仮説検定)
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
問題6.12[母分散の信頼区間].
同時正規測定
${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$
$({\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$
$S_{[(\mu, \sigma)]})$
を考えよう.この測定によって,
測定値$x \in X ={\mathbb R}^n$が得られたとする.
$0 < \alpha \ll 1$とする.
このとき,次を満たす${D}_{x}^{1- \alpha; \Theta}( \subseteq \Theta)$で,「出来るだけ小さいもの($\mu$に依存してもよい)」を見つけよ
