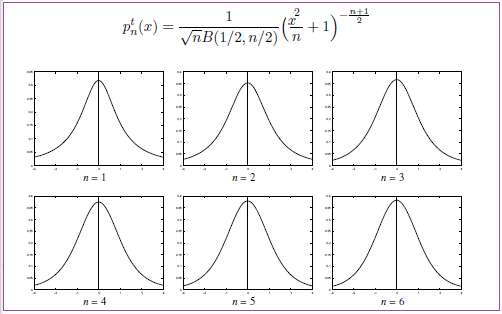
例 6.18 [Student $t$-分布].
同時正規測定
${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$
$({\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$
$S_{[(\mu, \sigma)]})$
(in $L^\infty({\mathbb R} \times {\mathbb R}_+)$)
を考える.
したがって,
状態空間$\Omega = {\mathbb R} \times {\mathbb R}_+$,
測定値空間$X={\mathbb R}^n$とする.
パラメータ空間$\Theta$を
$\Theta={\mathbb R}$として,
半距離
$d_\Theta^x (\forall x \in X)$
を次のように定める.
\begin{align}
d_\Theta^x (\theta_1, \theta_2)
=
\frac{|\theta_1-\theta_2|}{{\overline{\sigma}'(x)}/\sqrt{n}}
\quad
\qquad
(\forall x \in X={\mathbb R}^n,
\forall \theta_1, \theta_2 \in \Theta={\mathbb R}
)
\tag{6.76}
\end{align}
ここに,${\overline{\sigma}'(x)}=\sqrt{\frac{n}{n-1}}\overline{\sigma}(x)$である.
また,
システム量$\pi:\Omega(={\mathbb R} \times {\mathbb R}_+)
\to
\Theta(={\mathbb R})$
を次のように定める.
\begin{align}
\Omega(={\mathbb R} \times {\mathbb R}_+)
\ni \omega
=
(\mu, \sigma )
\mapsto \pi (\mu, \sigma )
=
\mu
\in
\Theta(={\mathbb R})
\tag{6.77}
\end{align}
推定量
$E:X(={\mathbb R}^n) \to \Theta(={\mathbb R})$
を次のように定める.
\begin{align}
E(x)=E(x_1, x_2, \ldots , x_n )
=
\overline{\mu}(x)
=
\frac{x_1 + x_2 + \cdots + x_n}{n}
\tag{6.78}
\end{align}
帰無仮説$H_N$
$(\subseteq
\Theta=
{\mathbb R} )
)$
を次のように定める:
\begin{align}
H_N= \{\mu_0\}
\tag{6.79}
\end{align}
任意の
$ \omega=(\mu_0, \sigma ) ({}\in \Omega=
{\mathbb R} \times {\mathbb R}_+ )$に対して,
次を得る.
\begin{align}
&
[G^n(\{ x \in X \;:\;
d^x_\Theta ( E(x) , \pi( \omega ) )
\ge \eta
\}
)](\omega )
\nonumber
\\
=&
[G^n(\{ x \in X \;:\;
\frac{
|\overline{\mu}(x)- \mu_0 |}{
{{\overline{\sigma}'(x)}/\sqrt{n}}
}
\ge \eta
\}
)](\omega )
\nonumber
\\
=
&
\frac{1}{({{\sqrt{2 \pi }\sigma{}}})^n}
\underset{
\eta
\le
\frac{
|\overline{\mu}(x)- \mu_0 |}{
{{\overline{\sigma}'(x)}/\sqrt{n}}
}
}{\int \cdots \int}
\exp[{}- \frac{\sum_{k=1}^n ({}{}{x_k} - {}{\mu_0} {})^2
}
{2 \sigma^2} {}] d {}{x_1} d {}{x_2}\cdots dx_n
\nonumber
\\
=
&
\frac{1}{({{\sqrt{2 \pi }{}}})^n}
\underset{
\eta
\le
\frac{
|\overline{\mu}(x) |}{
{{\overline{\sigma}'(x)}/\sqrt{n}}
}
}
{\int \cdots \int}
\exp[{}- \frac{\sum_{k=1}^n ({}{}{x_k} {} {})^2
}
{2 } {}] d {}{x_1} d {}{x_2}\cdots dx_n
\nonumber
\\
6.6.2: 信頼区間
=
&
1-
\int_{-\eta}^{\eta
}
p^t_{n-1}(x)
dx
\tag{6.80}
\end{align}
ここに,
$p^t_{n-1}$
は自由度$(n-1)$の$t$-分布の確率密度関数である.
方程式
\begin{align*}
1-\alpha
=
\int_{-\eta^\alpha_{\omega}}^{\eta^\alpha_{\omega}
}
p^t_{n-1}(x)
dx
\end{align*}
を解いて,
$\eta^\alpha_{\omega}$
$=t(\alpha/2)$
を得る.
問題:
$x_1, x_2, .... x_n $を正規分布$N(\mu, \sigma )$
(母平均$\mu$は未知、母分散$\sigma$は未知)から得られたデータとする。
このとき、我々の問題は
である。
この問題を量子言語に翻訳すると、以下のようになる。
| $\bullet$ | 「$\mu \in {D}_{x}^{1- \alpha; \Theta}$」である確率が,$1-\alpha$以上である. |
$L^\infty({\mathbb R} \times {\mathbb R}_+)$ 内の 同時正規測定 ${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$ $({\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$ $S_{[(\mu, \sigma)]})$ の測定値を $x ( \in {\mathbb R}^n )$とする. $({}\gamma{})$-信頼区間 $D_x^{\gamma, \Theta}$ は次のようになる. \begin{align} D_x^{\gamma, \Theta} & = \{ \pi({\omega}) (\in \Theta) : \omega \in \Omega, \;\; d^x_\Theta ({}E(x), \pi(\omega ) ) \le \eta^\gamma_{\omega } \} \nonumber \\ & = \{ \mu \in \Theta(={\mathbb R}) \;:\; \overline{\mu}(x) - \frac{{\overline{\sigma}'(x)}}{\sqrt{n}} t((1- \gamma)/2) \le \mu \le \overline{\mu}(x) + \frac{{\overline{\sigma}'(x)}}{\sqrt{n}} t((1- \gamma)/2) \} \\ & \tag{6.81} \end{align} または, \begin{align} D_x^{\gamma, \Omega} & = \{ {\omega} =(\mu, \sigma ) (\in \Omega) : \omega \in \Omega, \;\; d^x_\Theta ({}E(x), \pi(\omega ) ) \le \eta^\gamma_{\omega } \} \nonumber \\ & = \{ {\omega} =(\mu, \sigma ) (\in \Omega) \;:\; \overline{\mu}(x) - \frac{{\overline{\sigma}'(x)}}{\sqrt{n}} t((1- \gamma)/2) \le \mu \le \overline{\mu}(x) + \frac{{\overline{\sigma}'(x)}}{\sqrt{n}} t((1- \gamma)/2) \} \\ & \tag{6.82} \end{align}
6.6.3: 統計的仮説検定[帰無仮説$H_N=\{\mu_0\} ( \subseteq \Theta = {\mathbb R}$)の棄却域]
問題: $x_1, x_2, .... x_n $を正規分布$N(\mu, \sigma )$ (母平均$\mu$は未知、母分散$\sigma$は未知)から得られたデータとする。 このとき、我々の問題は
- $\mu=\mu_0$と仮定したとき、「$| \frac{x_1 + x_2 + ...+ x_n }{n} -\mu_0 | > \delta |$」は滅多に起きないような、最小の$\delta$をもとめよ
この問題を量子言語で書き換えると、以下のようになる。
同時正規測定 ${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$ $({\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$ $S_{[(\mu, \sigma)]})$ を考えよう.ここで, \begin{align*} \mu = \mu_0 \end{align*} と仮定しよう.すなわち,帰無仮説を$H_N=\{ \mu_0 \}$ $(\subseteq \Theta= {\mathbb R} ) )$ と仮定する.$0 < \alpha \ll 1$とする. このとき,次を満たす${\widehat R}_{{H_N}}^{\alpha; \Theta}( \subseteq \Theta)$で,「出来るだけ大きいもの(しかも,$\sigma$は依存しない)」を見つけよ
| $\bullet$ | ${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$ $({\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$ $S_{[(\mu_0, \sigma)]})$の測定値$x(\in{\mathbb R}^n )$が, \begin{align*} E(x) \in {\widehat R}_{{H_N}}^{\alpha; \Theta} \end{align*} を満たす確率は,$\alpha$以下である. |
帰無仮説$H_N(=\{\mu_0\})$を考える. このとき,棄却域${\widehat R}_{H_N}^{\alpha}$( 帰無仮説 $H_N(=\{\mu_0\})$の $({}\alpha{})$-棄却域 ) は以下のようになる.
\begin{align} {\widehat R}_{H_N}^{\alpha, \Theta} & = \bigcap_{\omega =(\mu, \sigma ) \in \Omega (={\mathbb R} \times {\mathbb R}_+) \mbox{ such that } \pi(\omega)= \mu \in {H_N}(=\{\mu_0\})} \{ E(x) (\in \Theta) : \;\; d^x_\Theta ({}E(x), \pi(\omega ) ) \ge \eta^\alpha_{\omega } \} \nonumber \\ & = \{\overline{\mu}(x) \in \Theta(={\mathbb R}) \;:\; \frac{ |\overline{\mu}(x)- \mu_0 |}{ {{\overline{\sigma}'(x)}/\sqrt{n}} } \ge t(\alpha/2) \} \nonumber \\ & = \{\overline{\mu}(x) \in \Theta(={\mathbb R}) \;:\; \mu_0 \le \overline{\mu}(x) - \frac{{\overline{\sigma}'(x)}}{\sqrt{n}} t(\alpha/2) \mbox{ or } \overline{\mu}(x) + \frac{{\overline{\sigma}'(x)}}{\sqrt{n}} t(\alpha/2) \le \mu_0 \} \\ & \tag{6.83} \end{align}または,
\begin{align} {\widehat R}_{H_N}^{\alpha,X} & = \bigcap_{\omega =(\mu, \sigma ) \in \Omega (={\mathbb R} \times {\mathbb R}_+) \mbox{ such that } \pi(\omega)= \mu \in {H_N}(=\{\mu_0\})} \{ x \in X : \;\; d^x_\Theta ({}E(x), \pi(\omega ) ) \ge \eta^\alpha_{\omega } \} \nonumber \\ & = \{ x \in X ={\mathbb R}^n \;:\; \frac{ |\overline{\mu}(x)- \mu_0 |}{ {{\overline{\sigma}'(x)}/\sqrt{n}} } \ge t(\alpha/2) \} \nonumber \\ & = \{ x \in X ={\mathbb R}^n \;:\; \mu_0 \le \overline{\mu}(x) - \frac{{\overline{\sigma}'(x)}}{\sqrt{n}} t(\alpha/2) \mbox{ or } \overline{\mu}(x) + \frac{{\overline{\sigma}'(x)}}{\sqrt{n}} t(\alpha/2) \le \mu_0 \} \\ & \tag{6.84} \end{align}6.6.4: 仮説検定[帰無仮説 $H_N=(- \infty , \mu_0]( \subseteq \Theta = {\mathbb R}$)]
問題: $x_1, x_2, .... x_n $を正規分布$N(\mu, \sigma )$ (母平均$\mu$は未知、母分散$\sigma$は未知)から得られたデータとする。 このとき、我々の問題は
- $\mu \le \mu_0$と仮定したとき、「$ \frac{x_1 + x_2 + ...+ x_n }{n} -\mu_0 > \delta |$」は滅多に起きないような、最小の$\delta$をもとめよ
である。
この問題を量子言語で書き換えると、以下のようになる。
同時正規測定 ${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$ $({\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$ $S_{[(\mu, \sigma)]})$ を考えよう.ここで, \begin{align*} \mu \in ( - \infty, \mu_0] \end{align*} と仮定しよう.すなわち,帰無仮説を$H_N=( - \infty, \mu_0] $ $(\subseteq \Theta= {\mathbb R} ) )$ と仮定する.$0 < \alpha \ll 1$とする. このとき,次を満たす${\widehat R}_{{H_N}}^{\alpha; \Theta}( \subseteq \Theta)$で,「出来るだけ大きいもの(しかも,$\sigma$は依存しない)」を見つけよ
| $\bullet$ | ${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$ $({\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$ $S_{[(\mu_0, \sigma)]})$の測定値$x(\in{\mathbb R}^n )$が, \begin{align*} E(x) \in {\widehat R}_{{H_N}}^{\alpha; \Theta} \end{align*} を満たす確率は,$\alpha$以下である. |
帰無仮説$H_N$を
\begin{align*}
H_N = (- \infty , \mu_0],
\end{align*}
とする.
したがって,半距離を次のように定める.
\begin{align}
d_\Theta^x (\theta_1, \theta_2)
=
\begin{cases}
\frac{|\theta_1-\theta_2|}{{\overline{\sigma}'(x)}/\sqrt{n}}
\quad
&
(
\forall \theta_1, \theta_2 \in \Theta={\mathbb R}
\mbox{ such that }
\mu_0 \le \theta_1, \theta_2
)
\\
\frac{\max \{ \theta_1, \theta_2 \}-\mu_0}{{\overline{\sigma}'(x)}/\sqrt{n}}
\quad
&
(
\forall \theta_1, \theta_2 \in \Theta={\mathbb R}
\mbox{ such that }
\min \{ \theta_1, \theta_2 \}
\le
\mu_0 \le \max \{ \theta_1, \theta_2 \}
)
\\
0
&
(
\forall \theta_1, \theta_2 \in \Theta={\mathbb R}
\mbox{ such that }
\theta_1, \theta_2
\le \mu_0
)
\end{cases}
\\
&
\tag{6.85}
\end{align}
とする.
このとき,$({}\alpha{})$-棄却域${\widehat R}_{H_N}^{\alpha, \Theta}$
は以下のようになる.
\begin{align}
{\widehat R}_{H_N}^{\alpha, \Theta}
&
=
\bigcap_{\omega =(\mu, \sigma ) \in \Omega (={\mathbb R} \times {\mathbb R}_+) \mbox{ such that }
\pi(\omega)= \mu \in {H_N}(=(- \infty , \mu_0])}
\{
E(x)
(\in
\Theta)
:
\;\;
d^x_\Theta ({}E(x),
\pi(\omega )
)
\ge
\eta^\alpha_{\omega }
\}
\nonumber
\\
&
=
\{\overline{\mu}(x) \in \Theta(={\mathbb R})
\;:\;
\mu_0 \le
\overline{\mu}(x)
-
\frac{{\overline{\sigma}'(x)}}{\sqrt{n}}
t(\alpha)
\}
\tag{6.86}
\end{align}
または,
\begin{align}
{\widehat R}_{H_N}^{\alpha, X}
&
=
\bigcap_{\omega =(\mu, \sigma ) \in \Omega (={\mathbb R} \times {\mathbb R}_+) \mbox{ such that }
\pi(\omega)= \mu \in {H_N}(=(- \infty , \mu_0])}
\{
x
(\in
X
={\mathbb R}^n)
\; :\;
d^x_\Theta ({}E(x),
\pi(\omega )
)
\ge
\eta^\alpha_{\omega }
\}
\nonumber
\\
&
=
\{
x
(\in
X
={\mathbb R}^n)
\; :\;
\mu_0 \le
\overline{\mu}(x)
-
\frac{{\overline{\sigma}'(x)}}{\sqrt{n}}
t(\alpha)
\}
\tag{6.87}
\end{align}
注意6.25仮説検定にはいろいろな流儀がある. 一番自然なのは尤度比検定である。 量子言語による尤度比検定については,何度もチャレンジ(下記(a),(b)等)しているがなかなか普及しない.やはり,「自然さ」よりも「使いやすさ」なのだろう.
| [a]: | S. Ishikawa, "Mathematical Foundations of measurement theory,"Keio University Press Inc. 2006. ( download free) |
| [b]: | S. Ishikawa, "A measurement Theoretical Foundation of Statistics" Applied Mathematics, Vol. 3, No. 3, 2012, pp. 283-292. ( download free) |
