10.2: 因果関係─火の無いところに,煙は立たない
10.2.1:ハイゼンベルグ描像とシュレーディンガー描像
まず、次を確認しておこう。
(A):一般基本構造と状態空間
-
一般基本構造:$[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$と状態
注意10.3 [$\overline{\mathcal A}_\ast \subseteq {\mathcal A}^*$]
基本構造
$[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$
を考えよう。
各
$\rho \in \overline{\mathcal A}_\ast$,
$F \in {\mathcal A} (\subseteq \overline{\mathcal A}
\subseteq B(H) )$に対して, 次は明らかに成立する:
\begin{align}
\Big|
_{\stackrel{}{\overline{\mathcal A}_* }}\Big(\rho, F \Big)_{\stackrel{}{\overline{\mathcal A} }}
\Big|
\le
C \| F\|_{B(H)}
=
C \| F\|_{\mathcal A}
\qquad
\tag{10.3}
\end{align}
よって、
$\rho \in {\mathcal A}^*$.
すなわち,
(10.3)の意味で,
\begin{align}
\overline{\mathcal A}_\ast \subseteq {\mathcal A}^*
\tag{10.4}
\end{align}
となる。
$\rho (\in \overline{\mathcal A}_* )$
を
${\mathcal A}^*$の元と見なすとき、
$\widehat{\rho}$と記す. すなわち,
\begin{align}
_{\stackrel{}{\overline{\mathcal A}_* }}\Big(\rho, F \Big)_{\stackrel{}{\overline{\mathcal A} }}
=
_{\stackrel{}{{\mathcal A}^* }}\Big(\widehat{\rho}, F \Big)_{\stackrel{}{{\mathcal A} }}
\qquad
(\forall F \in {\mathcal A} (\subseteq \overline{\mathcal A}))
\tag{10.5}
\end{align}
となる。
定義10.4 [ マルコフ因果作用素(=Causal operator)]
二つの基本構造
$[{\mathcal A}_1 \subseteq \overline{\mathcal A}_1 ]_{B(H_1)}$
と
$[{\mathcal A}_2 \subseteq \overline{\mathcal A}_2 ]_{B(H_2)}$
を考える.
連続線形作用素$\Phi_{1,2}:\overline{\mathcal A}_2
\to \overline{\mathcal A}_1 $
が次の
(i)$\text{---}$(iv)を満たすとき,$\Phi_{1,2}$
を
因果作用素
(または,
マルコフ因果作用素,
因果関係のハイゼンベルグ描像)と呼ぶ:
| $\mbox{(i):}$ |
$F_2 \in \overline{\mathcal A}_2 \;\; F_2 {\; \geqq \;}0$
$\Longrightarrow$
$\Phi_{12}F_2 {\; \geqq \;}0$
|
| $\mbox{(ii):}$ |
$\Phi_{12} I_{\overline{\mathcal A}_2} =I_{\overline{\mathcal A}_1} $
$\qquad$
(ここに,$I_{\overline{\mathcal A}_1} (\in {\overline{\mathcal A}_1} )$
は恒等元)
|
| $\mbox{(iii):}$ |
次を満たす連続線形作用素$({\Phi}_{1,2})_*:(\overline{\mathcal A}_1)_*
\to ( \overline{\mathcal A}_2)_* $
が存在する
\begin{align}
&
\mbox{(a)} \quad
{}_{\stackrel{{}}{(\overline{\mathcal A}_1)_* }}\Big(\rho_1, \Phi_{1,2} F_2 \Big){}_{\stackrel{{}}{\overline{\mathcal A}_1 }}
=
{}_{\stackrel{{}}(\overline{\mathcal A}_2)_* }\Big( ({\Phi}_{1,2})_\ast \rho_1, F_2\Big){}_{\stackrel{{}}{\overline{\mathcal A}_2 }}
\qquad %\hspace{2cm}
(\forall \rho_1 \in (\overline{\mathcal A}_1)_*,
\forall F_2 \in \overline{\mathcal A}_2 )
\\
&
\tag{10.6}
\\
&\mbox{(b)} \quad
({\Phi}_{1,2})_\ast (\overline{\frak S}^m( ( \overline{\mathcal A}_1)_*) )
\subseteq
\overline{\frak S}^m((\overline{\mathcal A}_2)_*)
\tag{10.7}
\end{align}
この連続線形作用素$({\Phi}_{1,2})_*$
を${\Phi}_{1,2}$の
前双対因果作用素
(
または,
マルコフ前双対因果作用素,
(因果関係のシュレーディンガー描像)
と呼ぶ.
|
| $\mbox{(iv):}$ |
$\Phi_{1,2}:{\mathcal A}_2 \to {\mathcal A}_1$で,
次を満たす連続線形作用素${\Phi}_{1,2}^*:{\mathcal A}_1^*
\to {\mathcal A}_2^*
$
が存在する.
\begin{align}
&
\mbox{(a)} \quad
{}_{\stackrel{{}}{(\overline{\mathcal A}_1)_* }}\Big(\rho_1, \Phi_{1,2} F_2 \Big){}_{\stackrel{{}}{\overline{\mathcal A}_1 }}
=
{}_{\stackrel{{}}{\mathcal A}_2^* }\Big( {\Phi}_{1,2}^\ast \widehat{\rho}_1, F_2\Big){}_{\stackrel{{}}{{\mathcal A}_2 }}
\qquad %\hspace{2cm}
(\forall \rho_1 = \widehat{\rho}_1 \in (\overline{\mathcal A}_1)_*
(\subseteq {\mathcal A}_1^*),
\forall F_2 \in {\mathcal A}_2 )
\\
&
\tag{10.8}
\\
&
\mbox{(b)} \quad
({\Phi}_{1,2})^* ({\frak S}^p({\mathcal A}_1^*) )
\subseteq
{\frak S}^m ({\mathcal A}_2^*)
\tag{10.9}
\end{align}
この連続線形作用素${\Phi}_{1,2}^*$
は${\Phi}_{1,2}$の
双対因果作用素
(
または,マルコフ双対因果作用素,
因果関係のシュレーディンガー描像)
と呼ぶ.
|
特に,
次を満たすとき,
因果作用素${\Phi}_{1,2}$を
決定的因果作用素
と呼ぶ.
\begin{align}
({\Phi}_{1,2})^* ({\frak S}^p({\mathcal A}_1^*) )
\subseteq
{\frak S}^p({\mathcal A}_2^*)
\tag{10.10}
\end{align}
| $\fbox{注釈10.3}$ |
[古典系の因果作用素]
古典系の基本構造
$[C_0(\Omega_1) \subseteq L^\infty (\Omega_1, \nu_1 )]_{B(H_1)}$
と
$[C_0(\Omega_2) \subseteq L^\infty (\Omega_2, \nu_2 )]_{B(H_2)}$
を考える.
連続線形作用素$\Phi_{1,2}:L^\infty (\Omega_2)
\to L^\infty (\Omega_1) $
が次の
(i)$\text{---}$(iii)を満たすとき,$\Phi_{1,2}$
を
因果作用素
( または,
マルコフ因果作用素,
因果関係のハイゼンベルグ描像)と呼ぶ:
| $\mbox{(i):}$ |
$f_2 \in L^\infty (\Omega_2), \;\; f_2 {\; \geqq \;}0$
$\Longrightarrow$
$\Phi_{12}f_2 {\; \geqq \;}0$
|
| $\mbox{(ii):}$ |
$\Phi_{12} 1_2 = 1_1$
ここに,
$1_k (\omega_k ) = 1$
$(
\forall \omega_k \in \Omega_k, k=1,2)$
|
| $\mbox{(iii):}$ |
次を満たす連続線形作用素$({\Phi}_{1,2})_\ast :L^1 (\Omega_1)
\to L^1_{}(\Omega_2) $
が存在する:
|
\begin{align*}
&
\int_{\Omega_1} [\Phi_{1,2} f_2](\omega_1) \;\;\rho_1 ( \omega_1 )
\nu_1( d \omega_1 )
=
\int_{\Omega_2} f_2(\omega_2)
\;\;
[({\Phi}_{1,2})_\ast \rho_1](\omega_2 ) \nu_2 ( d \omega_2 )
\\
&
(\forall \rho_1 \in L^1 (\Omega_1),
\forall f_2 \in L^\infty (\Omega_2))
\end{align*}
| $\quad$ |
この連続線形作用素$({\Phi}_{1,2})_\ast$
を${\Phi}_{1,2}$の前双対因果作用素(
または,マルコフ双対因果作用素,
因果関係のシュレーディンガー描像)
と呼ぶ.
|
| $\mbox{(iv):}$ |
$\Phi_{1,2}:C_0(\Omega_2 ) \to C_0(\Omega_1 )$で,
次を満たす連続線形作用素${\Phi}_{1,2}^\ast :{\mathcal M} (\Omega_1)
\to {\mathcal M}(\Omega_2) $
が存在する:
\begin{align*}
&
{}_{\stackrel{{}}{L^1(\Omega_1) }}\Big(\rho_1, \Phi_{1,2} F_2 \Big){}_{\stackrel{{}}{L^\infty(\Omega_1) }}
=
{}_{\stackrel{{}}{{\mathcal M}(\Omega_2) }}\Big( {\Phi}_{1,2}^\ast \widehat{\rho}_1, F_2\Big){}_{\stackrel{{}}{{C_0}(\Omega_2) }}\\
&
\qquad
(\forall \rho_1=\widehat{\rho}_1 \in {\mathcal M}(\Omega_1),
\forall F_2 \in {C_0}(\Omega_2) )
\end{align*}
ここに,
$\widehat{\rho}_1(D)= \int_D \rho_1 ( \omega_1) \nu_1(d \omega_1)$
$(\forall D \in {\mathcal B}_{\Omega_1} )$.
この連続線形作用素$({\Phi}_{1,2})_\ast$
を${\Phi}_{1,2}$の前双対因果作用素(
または,
マルコフ双対因果作用素,
(因果関係のシュレーディンガー描像})
と呼ぶ.
|
特に,
次を満たすような
連続写像$\phi_{1,2}:\Omega_1 \to \Omega_2$
が存在するとき,
因果作用素${\Phi}_{1,2}$を
決定的因果作用素
と呼ぶ.
\begin{align}
[\Phi_{1,2}f_2](\omega_1)
=
f_2(\phi_{1,2}(\omega_1))
\quad
(\forall f_2 \in C(\Omega_2 ), \forall \omega_1
\in \Omega_1 )
\tag{10.11}
\end{align}
また,この連続写像$\phi_{1,2}:\Omega_1 \to \Omega_2$を
決定的因果写像と呼ぶ.当然のことであるが,
\begin{align*}
\Omega_1
\approx
{\frak S}^p(C_0(\Omega_1)^*) \ni
\delta_{\omega_1}
\xrightarrow[\Phi_{12}^*]{} \delta_{\phi_{12}(\omega_1)}
\in
{\frak S}^p(C_0(\Omega_2)^*)
\approx
\Omega_2
\end{align*}
が成り立つ.
|
-
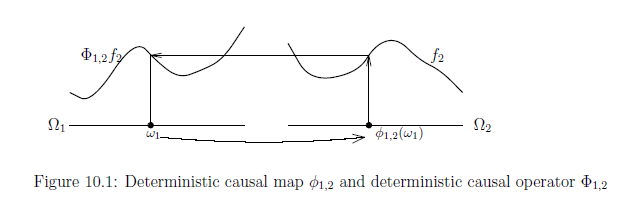
注意点:
| $(\sharp_1):$ |
写像は「点$\mapsto$点」で、簡単で中学生でもわかるぐらいで、
シュレーディンガー描像
と思えばよい。
|
| $(\sharp_2):$ |
作用素は「関数$\mapsto$関数」で、考えにくいが、
ハイゼンベルグ描像
と思えばよい。
|
しかし、不思議なことに、ハイゼンベルグ描像の方が使い出がある。
定理 10.5 [連続写像と決定的因果写像(deterministic causal map)]
[連続写像=決定的因果写像].
連続写像$\phi_{1,2}:\Omega_1 \to \Omega_2$
を考える.
作用素${\Phi}_{1,2}
:L^\infty (\Omega_2, \nu_2) \to L^\infty (\Omega_1, \nu_1)$を
(10.11)式
のように,
すなわち,
次のように定義する:
\begin{align*}
&
[\Phi_{1,2}f_2](\omega_1)
=
f_2(\phi_{1,2}(\omega_1))
\quad
(\forall f_2 \in L^\infty (\Omega_2 ), \forall \omega_1
\in \Omega_1 )
\end{align*}
このとき,作用素${\Phi}_{1,2}
:L^\infty (\Omega_2) \to L^\infty (\Omega_1)$は
決定的因果作用素
である.
したがって,
「連続写像=決定的因果写像」
と思ってよい.
証明$\;\;$
双対因果作用素${\Phi}^*_{1,2}:{\cal M}_{}(\Omega_1)
\to {\cal M}_{}(\Omega_2) $
の存在を示せば十分であるが,
これは
\begin{align}
[{\Phi}^*_{1,2}
\widehat{\rho}_1]
(D_2)
=
\widehat{\rho}_1 ( \phi_{12}^{-1}(D_2))
\qquad
(\forall D_2 \in {\cal B}_{\Omega_2},
\forall \widehat{\rho}_1 \in {\cal M}(\Omega_1) )
\tag{10.12}
\end{align}
と定めればよい.
$\square \quad$
定理 10.6
${\Phi}_{1,2}:L^\infty (\Omega_2)
\to L^\infty (\Omega_1) $
を{決定的因果作用素}とする.
このとき次が成り立つ:
\begin{align*}
{\Phi}_{1,2} (f_2 \cdot g_2 )
=
{\Phi}_{1,2} (f_2 )
\cdot
{\Phi}_{1,2} (g_2 )
\qquad
(\forall f_2, \forall g_2 \in L^\infty (\Omega_2 ))
\end{align*}
証明$\;\;$
$f_2$
と
$g_2$
を
$L^\infty (\Omega_2)$の任意の元とする.
このとき,決定的因果作用素${\Phi}_{1,2}$
の決定的因果写像を
$\phi_{1,2}:\Omega_1 \to \Omega_2$
として,次を得る:
\begin{align*}
&
[{\Phi}_{1,2} (f_2 \cdot g_2 )]
(\omega_1)
=
(f_2 \cdot g_2 )(\phi_{1,2}{(}\omega_1))
=
f_2(\phi_{1,2}{(}\omega_1))
\cdot
g_2(\phi_{1,2}{(}\omega_1))
\\
=
&
[{\Phi}_{1,2} (f_2 )]
(\omega_1)
\cdot
[{\Phi}_{1,2} (g_2 )]
(\omega_1)
=
[{\Phi}_{1,2} (f_2 )
\cdot
{\Phi}_{1,2} (g_2 )]
(\omega_1)
\qquad
(\forall \omega_1 \in \Omega_1)
\end{align*}
よって,証明された.
$\square \quad$


