2つの状態空間$\Omega_1$
と
$\Omega_2$
を実直線${\mathbb R}$,すなわち,
$\Omega_1=\Omega_2={\mathbb R}$
として,測度$\nu_1$と$\nu_2$はルベーグ測度とする.
二つの古典系の基本構造:
例 10.8 [双対因果作用素・因果作用素]
2つの有限状態空間$\Omega_1$
と
$\Omega_2$
を,
$\Omega_1=\{ \omega_1^1, \omega_1^2, \omega_1^3 \}$
と
$\Omega_2=\{ \omega_2^1 , \omega_2^2\}$
と定める.
$\rho_1 (\in {\cal M}_{+1}(\Omega_1))$を,
点測度
$\delta_{(\cdot)}
(\in
{\cal M}_{+1}(\Omega_1)
)
$
を用いて,
\begin{align*}
\rho_1= a_1 \delta_{\omega_1^1} +a_2 \delta_{\omega_1^2} +a_3 \delta_{\omega_1^3}
\quad
(0{{\; \leqq \;}}a_1,a_2 ,a_3 {{\; \leqq \;}}1,
a_1+a_2 +a_3=1)
\end{align*}
で定める.
このとき,
双対因果作用素
${\Phi}^*_{1,2}: {\cal M}_{+1}(\Omega_1) \to {\cal M}_{+1}(\Omega_2)$
は
\begin{align*}
{\Phi}^*_{1,2}(\rho_1 ) = &
(c_{11}a_1+c_{12}a_2+c_{13}a_3)\delta_{\omega_2^1}
+
(c_{21}a_1+c_{22}a_2+c_{23}a_3)\delta_{\omega_2^2}
\\
\;
&
(0 {{\; \leqq \;}}c_{ij} {{\; \leqq \;}}1,
\sum\limits_{i=1}^2 c_{ij} =1)
\end{align*}
と表現できる.
ここで,同一視:${\cal M}(\Omega_1) {\; \approx \;} {\mathbb C}^3$,
${\cal M}(\Omega_2) {\; \approx \;} {\mathbb C}^2$,
すなわち,
\begin{align*}
&
{\cal M}(\Omega_1)
\ni
\alpha_1 \delta_{\omega_1^1} +\alpha_2 \delta_{\omega_1^2} +
\alpha_3 \delta_{\omega_1^3}
\underset{同一視}{\longleftrightarrow}
\left[\begin{array}{ll}
\alpha_1
\\
\alpha_2
\\
\alpha_3
\\
\end{array}\right]
\in {\mathbb C}^3
\\
&
{\cal M}(\Omega_2)
\ni
\beta_1 \delta_{\omega_2^1} +\beta_2 \delta_{\omega_2^2}
\underset{同一視}{\longleftrightarrow}
\left[\begin{array}{ll}
\beta_1
\\
\beta_2
\\
\end{array}\right]
\in {\mathbb C}^2
\end{align*}
を考える.
このとき,
\begin{align*}
&
{\Phi}^*_{1,2}(\rho_1 ) =
\beta_1\delta_{\omega_2^1}
+
\beta_2\delta_{\omega_2^1}
=
\left[\begin{array}{ll}
\beta_1
\\
\beta_2
\\
\end{array}\right],
\\
&
\rho_1
=
\alpha_1 \delta_{\omega_1^1} +\alpha_2 \delta_{\omega_1^2} +
\alpha_3 \delta_{\omega_1^3}
=
\left[\begin{array}{ll}
\alpha_1
\\
\alpha_2
\\
\alpha_3
\\
\end{array}\right]
\end{align*}
とおいて,
行列形式で書けば,
\begin{align*}
{\Phi}^*_{1,2} (\rho_1 ) =
\left[\begin{array}{ll}
\beta_1
\\
\beta_2
\\
\end{array}\right]
=
\left[\begin{array}{ll}
c_{11} & c_{12} & c_{13}
\\
c_{21} & c_{22} & c_{23}
\\
\end{array}\right]
\left[\begin{array}{ll}
\alpha_1
\\
\alpha_2
\\
\alpha_3
\\
\end{array}\right]
\end{align*}
次に,この双対因果作用素
${\Phi}^*_{1,2}: {\cal M}_{}(\Omega_1) \to {\cal M}_{}(\Omega_2)$
から,
因果作用素
$\Phi_{1,2}: L^\infty (\Omega_2, \nu_2) \to L^\infty (\Omega_1, \nu_1)$を構成しよう.
$\nu_1 (\{\omega_1^k\})=1$
$(\; k=1,2,3)$,
$\nu_2 (\{\omega_2^k\})=1$
$(\; k=1,2)$
としておく.
同一視:${L^\infty }(\Omega_1)
{\; \approx \;}
{\mathbb C}^3$,
${L^\infty }(\Omega_2) {\; \approx \;} {\mathbb C}^2$,
すなわち,
\begin{align*}
{L^\infty }(\Omega_1)
\ni
f_1
\underset{同一視}{\longleftrightarrow}
\left[\begin{array}{ll}
f_1 ( \omega_1^1)
\\
f_1 ( \omega_1^2)
\\
f_1 ( \omega_1^3)
\\
\end{array}\right]
\in {\mathbb C}^3,
\qquad
{L^\infty }(\Omega_2)
\ni
f_2
\underset{同一視}{\longleftrightarrow}
\left[\begin{array}{ll}
f_2 ( \omega_2^1)
\\
f_2 ( \omega_2^2)
\\
\end{array}\right]
\in {\mathbb C}^2
\end{align*}
を考える.
$f_2 \in L^\infty (\Omega_2)$,
$f_1 = \Phi_{1,2} f_2$として,
行列形式で書けば,
\begin{align*}
\left[\begin{array}{ll}
f_1(\omega_1^1)
\\
f_1(\omega_1^2)
\\
f_1(\omega_1^3)
\\
\end{array}\right]
=
f_1
=
\Phi_{1,2} (f_2 ) =
\left[\begin{array}{ll}
c_{11} & c_{21}
\\
c_{12} & c_{22}
\\
c_{13} & c_{23} &
\\
\end{array}\right]
\left[\begin{array}{ll}
f_2(\omega_2^1)
\\
f_2(\omega_2^2)
\\
\end{array}\right]
\end{align*}
となる.
したがって,双対因果作用素${\Phi}^*_{1,2}$と
因果作用素$\Phi_{1,2}$
の関係は,
行列表現をもつ場合
(すなわち,
$\Omega_1$
と
$\Omega_2$
が有限集合
の場合
)
は「転置」の関係になる.
例 10.9[決定双対因果作用素,決定的因果写像,決定的因果作用素]
上の例から引き継いで,
双対因果作用素
${\Phi}^*_{1,2}: {\cal M}(\Omega_1)
({\approx} {\mathbb C}^3)
\to {\cal M}(\Omega_2)
({\approx} {\mathbb C}^2)
$
が,
たとえば,
行列形式で,
\begin{align*}
{\Phi}^*_{1,2}(\rho_1 ) =
\left[\begin{array}{ll}
b_1
\\
b_2
\\
\end{array}\right]
=
\left[\begin{array}{ll}
0 & 1& 1
\\
1 & 0& 0
\\
\end{array}\right]
\left[\begin{array}{ll}
a_1
\\
a_2
\\
a_3
\\
\end{array}\right]
\end{align*}
と表現される場合は,決定双対因果作用素になる.
この
決定的因果作用素
$\Phi_{1,2}: C(\Omega_2) \to C(\Omega_1)$
を
行列形式で書けば,
となる.
もちろん,
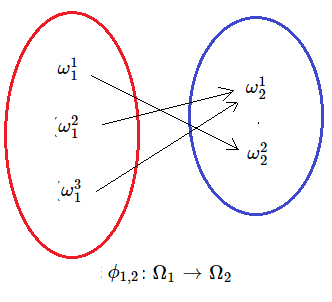
その決定的因果写像
$\phi_{1,2}: \Omega_1 \to \Omega_2$
は
\begin{align*}
\phi_{1,2}(\omega_1^1)= \omega_2^2,
\quad
\phi_{1,2}(\omega_1^2)= \omega_2^1,
\quad
\phi_{1,2}(\omega_1^3)= \omega_2^1
\quad
\end{align*}
で表される.
10.2.3: 因果作用素列─因果関係の連鎖
$(T,{{\; \leqq \;}})$ {{を}}木半順序集合, すなわち,半順序集合で,
任意の
$t_1, t_2, t_3 (\in T)$
に対して,
\begin{align*}
t_1 {{\; \leqq \;}}t_3,
\;\;
t_2 {{\; \leqq \;}}t_3
\Longrightarrow
t_1 {{\; \leqq \;}}t_2
\text{ または }
t_2 {{\; \leqq \;}}t_1
\end{align*}
を満たすとする.
$T^2_{\leqq}= \{ (t_1,t_2) \in T^2{}\; |\; t_1 {{\; \leqq \;}}t_2 \}$
とおく.
要素 $t_0 \in T$が,
条件:「$t_0 {{\; \leqq \;}}t$ ($\forall t \in T$)」
を満たすとき,$t_0 $を
$T$の
ルート
と呼ぶ.
このとき,
$(T,{{\; \leqq \;}})$
を
$(T(t_0),{{\; \leqq \;}})$
と書くこともある.
木半順序集合$T$が有限と仮定するならば,親写像$\pi{}: T \setminus \{ t_0 \} \to T$
を
$\pi (t{}) = \max \{ s \in T{}\; |\; s < t \}$
で定義できる.
ルート$t_0$
をもつ木半順序集合
$(T(t_0), {{\; \leqq \;}})$
は,
対
$(T{{=}} \{ t_0,t_1,\ldots, t_N\} , \pi:
T \setminus \{ t_0 \} \to T)$
で表現することもある.
この表現$(T{{=}} \{ t_0,t_1,\ldots, t_N\} , \pi:
T \setminus \{ t_0 \} \to T)$
を,
$(T(t_0), {{\; \leqq \;}})$
の{\bf 親写像表現}と呼ぶ.
定義10.10 [因果作用素列; 因果関係のハイゼンベルグ描像]
(i):
[前双対因果作用素列; 因果関係のシュレーディンガー描像]
族
$\{ ({\Phi}_{t_1,t_2})_*{}: $
$
(\overline{\mathcal A}_{t_1})_* \to
(\overline{\mathcal A}_{t_1})_*
\}_{(t_1,t_2) \in T^2_{\leqq}}$
を,
$\{ \Phi_{t_1,t_2}{}: $
${
\overline{\mathcal A}_{t_2}} \to {\overline{\mathcal A}{t_1}} \}_{(t_1,t_2) \in T^2_{\leqq}}$
の
前双対因果作用素列
(または,
因果関係列のシュレーディンガー描像)
という.
(ii):
[双対因果作用素列: 因果関係のシュレーディンガー描像]
族
$\{ {\Phi}^*_{t_1,t_2}{}: $
$
{\mathcal A}^\ast_{t_1} \to
{\mathcal A}^\ast_{t_1}
\}_{(t_1,t_2) \in T^2_{\leqq}}$
を,
$\{ \Phi_{t_1,t_2}{}: $
${
\overline{\mathcal A}_{t_2}} \to {\overline{\mathcal A}{t_1}} \}_{(t_1,t_2) \in T^2_{\leqq}}$
の
双対因果作用素列}
(または,
因果関係列のシュレーディンガー描像})
という.
シュレーディンガー描像
は直感的で手軽である。
シュレーディンガー描像$\{ {\Phi}^*_{t_1,t_2}{}: $
$
{\mathcal A}^\ast_{t_1} \to
{\mathcal A}^\ast_{t_1}
\}_{(t_1,t_2) \in T^2_{\leqq}}$
を考えて,
$t_1 (\in T)$において,
$C^*$-混合状態$\rho_{t_1}
(\in {\frak S}^m({\mathcal A}_{t_1}^*)$を想定すれば,
10.2.2: 簡単な例─有限状態空間ならば,因果作用素は行列表現可能
例 10.7 [決定的因果作用素,決定双対因果作用素,決定的因果写像
]
^2+3.png) \begin{align*}
[
C_0(\Omega_1(\equiv {\mathbb R}) ) \subseteq L^\infty (\Omega_1, \nu_1 ) \subseteq B(L^2 (\Omega_1, \nu_1 ))]
\end{align*}
\begin{align*}
[
C_0(\Omega_2(\equiv {\mathbb R})) \subseteq L^\infty (\Omega_2, \nu_2 ) \subseteq B(L^2 (\Omega_2, \nu_2 ))]
\end{align*}
を考える.
決定的因果写像
$\phi_{1,2} : \Omega_1 \to \Omega_2 $
を,
たとえば,二次関数:
\begin{align*}
\omega_2 = \phi_{1,2}(\omega_1 )= 3 (\omega_1)^2 +2
\qquad
(\forall \omega_1 \in \Omega_1 ={\mathbb R})
\end{align*}
で定める.
このとき,
点測度$\delta_{(\cdot)}$
を用いて書けば,
決定双対因果作用素
${\Phi}^*_{1,2}:{\cal M}_{}(\Omega_1)
\to {\cal M}_{}(\Omega_2) $
が次のように定義できる.
\begin{align*}
{\Phi}^*_{1,2} \delta_{\omega_1} = \delta_{3 (\omega_1)^2 +2}
\qquad
(\forall \omega_1 \in \Omega_1 )
\end{align*}
であり,
決定的因果作用素$\Phi_{1,2}:L^\infty (\Omega_2)
\to L^\infty (\Omega_1) $
は,
\begin{align*}
[\Phi_{1,2}
(f_2)](\omega_1 )
=
f_2(3 (\omega_1)^2 +2)
\qquad
(\forall f_2 \in L^\infty (\Omega_2), \forall \omega_1 \in \Omega_1 )
\end{align*}
によって定まる.
\begin{align*}
[
C_0(\Omega_1(\equiv {\mathbb R}) ) \subseteq L^\infty (\Omega_1, \nu_1 ) \subseteq B(L^2 (\Omega_1, \nu_1 ))]
\end{align*}
\begin{align*}
[
C_0(\Omega_2(\equiv {\mathbb R})) \subseteq L^\infty (\Omega_2, \nu_2 ) \subseteq B(L^2 (\Omega_2, \nu_2 ))]
\end{align*}
を考える.
決定的因果写像
$\phi_{1,2} : \Omega_1 \to \Omega_2 $
を,
たとえば,二次関数:
\begin{align*}
\omega_2 = \phi_{1,2}(\omega_1 )= 3 (\omega_1)^2 +2
\qquad
(\forall \omega_1 \in \Omega_1 ={\mathbb R})
\end{align*}
で定める.
このとき,
点測度$\delta_{(\cdot)}$
を用いて書けば,
決定双対因果作用素
${\Phi}^*_{1,2}:{\cal M}_{}(\Omega_1)
\to {\cal M}_{}(\Omega_2) $
が次のように定義できる.
\begin{align*}
{\Phi}^*_{1,2} \delta_{\omega_1} = \delta_{3 (\omega_1)^2 +2}
\qquad
(\forall \omega_1 \in \Omega_1 )
\end{align*}
であり,
決定的因果作用素$\Phi_{1,2}:L^\infty (\Omega_2)
\to L^\infty (\Omega_1) $
は,
\begin{align*}
[\Phi_{1,2}
(f_2)](\omega_1 )
=
f_2(3 (\omega_1)^2 +2)
\qquad
(\forall f_2 \in L^\infty (\Omega_2), \forall \omega_1 \in \Omega_1 )
\end{align*}
によって定まる.
 \begin{align*}
\left[\begin{array}{ll}
f_1(\omega_1^1)
\\
f_1(\omega_1^2)
\\
f_1(\omega_1^3)
\\
\end{array}\right]
=
f_1
=
\Phi_{1,2} (f_2 ) =
\left[\begin{array}{ll}
0 & 1
\\
1& 0
\\
1 & 0 &
\\
\end{array}\right]
\left[\begin{array}{ll}
f_2(\omega_2^1)
\\
f_2(\omega_2^2)
\\
\end{array}\right]
\end{align*}
\begin{align*}
\left[\begin{array}{ll}
f_1(\omega_1^1)
\\
f_1(\omega_1^2)
\\
f_1(\omega_1^3)
\\
\end{array}\right]
=
f_1
=
\Phi_{1,2} (f_2 ) =
\left[\begin{array}{ll}
0 & 1
\\
1& 0
\\
1 & 0 &
\\
\end{array}\right]
\left[\begin{array}{ll}
f_2(\omega_2^1)
\\
f_2(\omega_2^2)
\\
\end{array}\right]
\end{align*}
図10.2
は,
$t_0$がルートで,
$\pi(t_3)=\pi(t_4)=t_2$,
$\pi(t_2)=\pi(t_5)=t_1$,
$\pi(t_1)=\pi(t_6)=\pi(t_7)=t_0$
の例である.
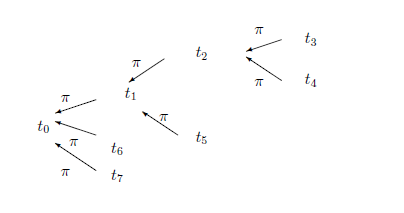
 $T$を木半順序集合とする.
各$ t \in T$に対して,
基本構造
\begin{align*}[ {\mathcal A}_t \subseteq \overline{\mathcal A}_t \subseteq B(H_t)]
\end{align*}
を考える.
{{}}族
$\{ \Phi_{t_1,t_2}{}: $
${
\overline{\mathcal A}_{t_2}} \to {\overline{\mathcal A}_{t_1}} \}_{(t_1,t_2) \in T^2_{\leqq}}$
$\Big($
または,
$\{$
${\overline{\mathcal A}_{t_2}
} \overset{\Phi_{t_1,t_2}}\to {\overline{\mathcal A}_{t_1}} \}_{(t_1,t_2) \in T^2_{\leqq}}$
とも記される
$\Big)$
は
次を満たすとき,
因果作用素列
(または,
因果関係列のハイゼンベルグ描像)
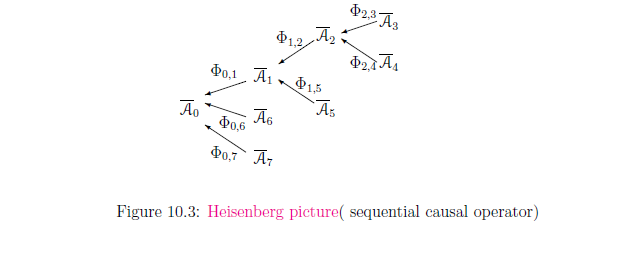
という(図10.3):
$T$を木半順序集合とする.
各$ t \in T$に対して,
基本構造
\begin{align*}[ {\mathcal A}_t \subseteq \overline{\mathcal A}_t \subseteq B(H_t)]
\end{align*}
を考える.
{{}}族
$\{ \Phi_{t_1,t_2}{}: $
${
\overline{\mathcal A}_{t_2}} \to {\overline{\mathcal A}_{t_1}} \}_{(t_1,t_2) \in T^2_{\leqq}}$
$\Big($
または,
$\{$
${\overline{\mathcal A}_{t_2}
} \overset{\Phi_{t_1,t_2}}\to {\overline{\mathcal A}_{t_1}} \}_{(t_1,t_2) \in T^2_{\leqq}}$
とも記される
$\Big)$
は
次を満たすとき,
因果作用素列
(または,
因果関係列のハイゼンベルグ描像)
という(図10.3):
$\mbox{(i):}$
任意の$(t_1,t_2) \in T^2_{\leqq}$に対して, 因果作用素
$\Phi_{t_1,t_2}{}: $
${
\overline{\mathcal A}_{t_2}} \to {\overline{\mathcal A}_{t_1}}$
が定義されて,
$\Phi_{t_1,t_2} \Phi_{t_2,t_3} = \Phi_{t_1,t_3}$
$(\forall (t_1,t_2)$,
$\forall (t_2,t_3) \in T^2_{\leqq})$
を満たす.
ここに,
$\Phi_{t,t} : {\overline{\mathcal A}_{t}} \to {\overline{\mathcal A}_{t}}$
は恒等作用素とする.
定義10.11

と思えばよい.
しかし,注意点は, 言語的コペンハーゲン解釈「状態は動かない」の帰結として,
$\bullet$
$
t_2 (\ge t_1)
$
における$C^*$-混合状態$\rho_{t_2}
(\in {\frak S}^m({\mathcal A}_{t_2}^*))$
は
\begin{align*}
\rho_{t_2}=\Phi_{t_1, t_2}^* \rho_{t_1}
\end{align*}
となる.
ということである. このことは,後で述べる.
$\bullet$
ハイゼンベルグ描像が正式で, シュレーディンガー描像は場合の手法
10.2.2: 簡単な例─有限状態空間ならば,因果作用素は行列表現可能
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
注意10.12 [ハイゼンベルグ描像が正式]
