「時空とは何か?」の問い掛けに対して、物理の観点からは健全な議論がされている。 しかし、哲学の観点からは情けないほどの非生産的議論が横行していて、「だから、哲学はダメなんだ」という世論の形成に一役買っているように思う。 哲学からのまともな議論は、「量子言語の時空」だけと思う。 以下にこれを説明しよう。
この節の議論は、次の論文からの抜粋である:
「時空とは,何か?」は、伝統的哲学だけでなくて、現代科学においても
最重要の未解決問題である。
本節では、この問題に量子言語の立場から解答を与える。
当然のことであるが、
-
世界記述法を提案したら、次は「時空とは,何か?」に答える
とか、
より正確には、
-
世界記述法を提案したら、その世界記述法で「時空」を記述する
が原則である。
ニュートンはこの原則を守ったが、ライプニッツは、
世界記述法の提案なしに、『時空とは,何か?』に答えてしまった。
この結果:
-
[ニュートン vs. ライプニッツ]において、ニュートンの勝利にような印象が残ってしまった
そうだとしても、
ニュートンの「実在的時空」に対抗して、
ライプニッツは
「形而上学的時空」
の科学的意義を直感したわけで、やはりすごい。
上記のようなことを、量子言語の立場から以下に議論する。
10.7.1:"空間とは何か?" と "時間とは何か?"
10.7.1.1: 量子言語によって、「空間」を如何にに記述するか?
以下に、最も単純な場合について考えよう。
たとえば、
| $(A):$ |
$
\qquad \qquad
\mbox{"空間"=${\mathbb R}_q$(一次元実空間)}
$
|
としよう。
古典系(B$_1$)と量子系(B$_2$)の両方を、次のように考える。
| $(B):$ |
$
\begin{cases}
\mbox{(B$_1$): 一次元実空間${\mathbb R}_q$}内の古典粒子
\\
\\
\mbox{(B$_2$): 一次元実空間${\mathbb R}_q$内の量子粒子}
\end{cases}
$
|
古典系の場合は、次の
状態
を想定して、
\begin{align*}
\mbox{
$(q,p)$
$=$
("位置", "運動量") $\in {{\mathbb R}_q \times {\mathbb R}_p }$
}
\end{align*}
であり、
古典基本構造:
| $(C_1):$ |
$
\qquad
[
C_0({\mathbb R}_q \times {\mathbb R}_p)
\subseteq
L^\infty ( {\mathbb R}_q \times {\mathbb R}_p)
\subseteq
B(
L^2 ( {\mathbb R}_q \times {\mathbb R}_p)
]
$
|
を得る。
また、量子系の場合は、量子基本構造:
| $(C_2):$ |
$
\qquad
[
{\mathcal C}(
L^2 ( {\mathbb R}_q )
\subseteq
B(
L^2 ( {\mathbb R}_q )
\subseteq
B(
L^2 ( {\mathbb R}_q )
]
$
|
からスタートすることは、今までに何度も述べた。。
まとめると、
つぎの一般基本構造:
| $(C):$ |
$
[{\mathcal A} \subseteq \overline{\mathcal A}
\subseteq
B(H)]
\begin{cases}
\mbox{(C$_1$):古典系
$
[
C_0({\mathbb R}_q \times {\mathbb R}_p)
\subseteq
L^\infty ( {\mathbb R}_q \times {\mathbb R}_p)
\subseteq
B(
L^2 ( {\mathbb R}_q \times {\mathbb R}_p)
]
$
}
\\
\\
\mbox{(C$_2$):量子系
$
[
{\mathcal C}(
L^2 ( {\mathbb R}_q )
\subseteq
B(
L^2 ( {\mathbb R}_q )
\subseteq
B(
L^2 ( {\mathbb R}_q )
]
$}
\end{cases}
$
|
を得たのであった
さて、量子言語では、基本構造からスタートするのだから、
"(A)$\Longrightarrow$(C)"の逆の議論をすればよい。
すなわち、次のように考えることになる。
\begin{align}
&
\mbox{
「空間」を量子言語で如何に記述するか?
}
\nonumber
\\
\Leftrightarrow
&
\mbox{
[(C):基本構造]から
[(A):空間]を如何に導出するか?
}
\tag{10.29}
\end{align}
これは次のステップによって実現される。
主張10.17「空間」を量子言語で如何に記述するか?
| $(D_1):$ |
基本構造:
\begin{align*}
[{\mathcal A} \subseteq \overline{\mathcal A}
\subseteq
B(H)]
\end{align*}
から
スタートする。
|
| $(D_2):$ |
ここで、次を満たす可換$C^*$-代数 ${\mathcal A}_0
(=C_0(\Omega ))$
を考える:
\begin{align*}
{\mathcal A}_0 \subseteq \overline{\mathcal A}
\end{align*}
|
| $(D_3):$ |
このとき、
スペクトラム
$\Omega$
$(\approx {\frak S}^p ({\mathcal A}_* ) )$
を使って、
"空間"
を表現する。
|
量子言語による解答は簡単で、これだけのことである。
たとえば,
| $(E_1):$ |
古典系の場合(C$_1$):
\begin{align*}
[
C_0({\mathbb R}_q \times {\mathbb R}_p)
\subseteq
L^\infty ( {\mathbb R}_q \times {\mathbb R}_p)
\subseteq
B(
L^2 ( {\mathbb R}_q \times {\mathbb R}_p))
]
\end{align*}
次の
可換$C^*$-代数$C_0({\mathbb R}_q )$:
\begin{align*}
C_0({\mathbb R}_q ) \subseteq L^\infty ({\mathbb R}_q \times {\mathbb R}_p )
\end{align*}
を考えて、
そのスペクトラムとして空間${\mathbb R}_q$
を得る。
|
| $(E_2):$ |
量子系の場合(C$_2$):
\begin{align*}
[
{\mathcal C}(
L^2 ( {\mathbb R}_q )
\subseteq
B(
L^2 ( {\mathbb R}_q ))
\subseteq
B(
L^2 ( {\mathbb R}_q ))
]
\end{align*}
次の
可換$C^*$-代数$C_0({\mathbb R}_q )$:
\begin{align*}
C_0({\mathbb R}_q ) \subseteq
B(
L^2 ( {\mathbb R}_q ))
\end{align*}
を考えて、
そのスペクトラムとして空間${\mathbb R}_q$
を得る。
|
10.7.1.2: 量子言語によって、「時間」を如何にに記述するか?
量子言語の中で、「時間」は以下のようになる。
主張10.18 [「時間」を量子言語で如何に記述するか?]
| $(F_1):$ |
木半順序集合$T$を考える(第14章では、無限木半順序集合を議論する). いつものように、
各$t \in T$に対して、基本構造
\begin{align*}
[{\mathcal A}_t \subseteq \overline{\mathcal A}_t \subseteq B(H_t)]
\end{align*}
を考える。
|
| $(F_2):$ |
ここで、ある部分線形順序集合
$T' (\subseteq T)$を考え、これで
"時間"を表現する。
|
量子言語による解答は簡単で、これだけのことである。
10.7.2: ライプニッツ=クラーク論争

前節の議論は
ライプニッツ=クラーク論争(1715--1716)の
ライプニッツの立場--
時空の関係説
--を思い出させる。
ライプニッツ=クラーク論争における
ライプニッツの立場とクラークの立場(=ニュートンの立場)を以下に整理しておく。
| $(G):$ |
[実在的時空]
ニュートンの絶対時空では、時空は
"もの"
の入れ物と考える。
したがって、
"もの"
が無かったとしても、時空は存在する。
|
他方、
| $(H):$ |
[形而上学的時空]
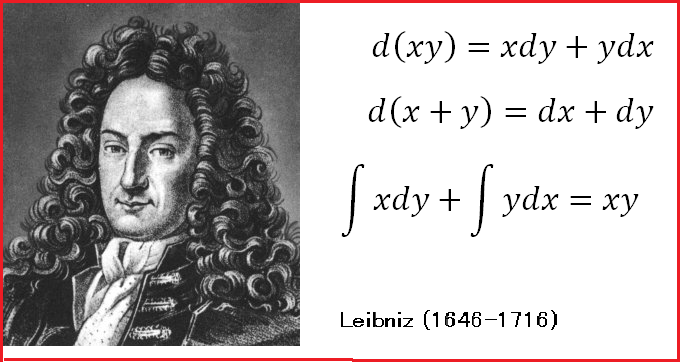 ライプニッツの関係説
は次を主張する。
ライプニッツの関係説
は次を主張する。
| $(H_1):$ |
空間の点は、
"もの"の状態の一種である.
|
| $(H_2):$ |
時間は、ものの推移の順序である。
|
したがって、
"もの"
が無ければ、時空は存在しない。
|
そうならば、次の対立関係を考えたくなる。
\begin{align*}
\underset{\mbox{(実在的観点)}}{\fbox{ニュートン($\approx$クラーク)}}
\quad
\underset{\mbox{v.s.}}{\longleftrightarrow}
\quad
\underset{\mbox{(言語的観点)}}{\fbox{ライプニッツ}}
\end{align*}
また、これは次の対立関係を連想させる:
\begin{align*}
\underset{\mbox{(実在的観点)}}{\fbox{アインシュタイン}}
\quad
\underset{\mbox{v.s.}}{\longleftrightarrow}
\quad
\underset{\mbox{(言語的観点)}}{\fbox{ボーア}}
\end{align*}
(cf.注釈4.4).
| $\fbox{注釈10.6}$ |
多くの科学者は次のように考えるかもしれない:
| $\quad$ |
ニュートンの主張は納得できる。
事実、これはアインシュタインに引き継がれた。
他方、
ライプニッツの主張はわかりにくいし、
科学的でない
|
しかしながら、
世界記述の発展史(Figure 1.1 in $\S$1.1)を思い出してもらいたい。
すなわち、
$
\begin{cases}
\mbox{(i)}:
\underset{\text{(実在的科学観)}}{\text{ニュートン、クラーク}}
&
\cdots
\overset{\text{(物理的時空)}}{
\underset{\text{"時空とは何か?"}}{
\fbox{実在的時空}}
}
\quad
\qquad
\text{(アインシュタイン等に継承される)}
\\
\\
\mbox{(ii)}:
\underset{\text{(言語的科学観)}}{\text{ライプニッツ}}
&
\cdots
\overset{\text{(量子言語の時空)}}{
\underset{\text{"時空を如何に表現するか?"}}{
\fbox{言語的時空}}
}
\;\;
\text{(スペクトラム、全順序集合)}
\end{cases}
$
ライプニッツの関係説は、明確でない部分もあるが
| $\bullet$ |
ライプニッツは、科学における
"形而上学的時空"
の重要さに気づいた
|
のだと考える。
しかしながら、次は注目すべきと思う。
| $(\sharp):$ |
ニュートンは、「ニュートン力学という言語」の下に、
時空の絶対説を主張した。
他方,
ライプニッツは、
「彼の言語」を提案せずに、
「日常言語」の中で、時空の関係説を主張した
|
これでは、ニュートンに分がある結末は目に見えていた。
ニュートンが「ニュートン力学」を発見する可能性より、
ライプニッツが「古典測定理論」を発見する可能性の方が大だったと思うが、
歴史はそうならなかった。
|
| $\fbox{注釈10.7}$ |
科学における大論争は、結局、
\begin{align*}
\underset{\mbox{ }}{\fbox{実在的科学観}}
\quad
\underset{\mbox{v.s.}}{\longleftrightarrow}
\quad
\underset{\mbox{(観念論)}}{\fbox{言語的科学観}}
\end{align*}
だけなのかもしれない。
異論があることは承知で、下表を主張したい:
一般には普遍論争は非常に分かりにくいと言われている。 二つのテーマ:
- 上の表の「実在的科学観(オッカム:世界が先で、言葉が後) vs. 言語的科学観(アンセルムス:言葉が先で、世界が後)」
-
二元論(トマス・アクィナス:三元論)
がゴッチャにされて議論されたという歴史的経緯があり、それをそのまま書いて、普遍論争の説明としている哲学書が多いからである。
|
| $\fbox{注釈10.8}$ |
時空の問題は、哲学の中心的問題で、多くの考察が残されている。
ここで、
"測定者の時間"
に関して多少のことを述べておこう。
言語的コペンハーゲン解釈によれば、
| $(\sharp_1):$ |
「いつどこで測定されたか?」は
ナンセンスである。「いつどこで測定されたか?」を認めてしまうと、
「ウィグナーの友人のパラドックス($\S$11.4)」が生じてしまう。
|
| $(\sharp_2):$ |
すなわち、
科学においては、「時制」は無意味である
|
| $(\sharp_3):$ |
つまり、
「測定者の時間は存在しない」
|
と主張する。
これは、マクタガートの主張に似ている。
すなわち、
-
マクタガートのパラドックス:
"時間は存在しない"
マクタガートのロジックは明確ではないが、
マクタガートは「主観時間(=
(e.g.,
アウグステゥヌスやベルグソンの時間
)は存在しない」
と主張しているとするならば、しかも、
「主観時間=測定者の時間」
と考えるならば、言語的コペンハーゲン解釈と同じことを主張しているとも
考えられる。
したがって,
| $(\sharp_3):$ |
マクタガートの主張やライプニッツの主張は、
言語的コペンハーゲン解釈の一つと考えたい。
|
一般に言えることであるが、
| $(\sharp_4):$ |
哲学(二元論的観念論)の失敗は(=哲学が役に立たなかった原因は)、
「言語を提案しなかった」ことである。
|
ウィトゲンシュタインが、
-
The limit of my language means the limit of my world
私の言語の限界が、私の世界の限界
と、「言語の本質性」を強調したにも拘わらずである。「重要」と言いながら、「なぜ作らなかったの?」と問いたくなるが、「言語哲学の不思議」と言う以外に言いようがない。
皮肉な言い方をするならば、
| $(\sharp_5):$ |
哲学者たちは、言語
(i.e.,
言語ルール1(測定:$\S$2.7)
と言語ルール(因果関係:$\S$10.3)
を知らずに、
"言語的コペンハーゲン解釈"
(="言語ルール 1 と 2 の使い方")
を議論していた
|
とも言える。
|

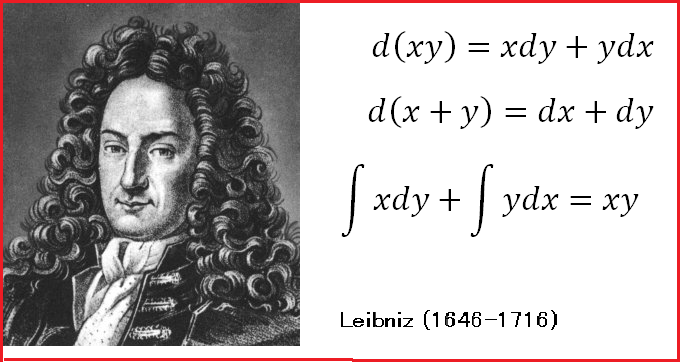 ライプニッツの関係説
は次を主張する。
ライプニッツの関係説
は次を主張する。



.png)
