この節では,$B(L^2({\mathbb R}))$内のド・ブロイのパラドックスの説明する
(
[2.10節:$B({\mathbb C}^2)$内のド・ブロイのパラドックス]
と実質的に同じであるが、この節の説明がド・ブロイのパラドックスの原型である
).
を考える.ここに,$m$は粒子の質量,$V$はポテンシャルエネルギーとする.
図示のため,${\mathbb R}^3$を${\mathbb R}$とする.
したがって,
ヒルベルト空間$H=L^2({\mathbb R}, dq)$を考える.
任意の時刻$t(\in {\mathbb R})$において,
$H_t=H$として,
量子系の基本構造
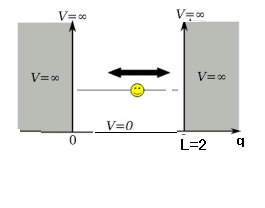
質量$m$の粒子$P$が,
箱(すなわち,
閉区間$[0,2]$)
に入っているとしよう.
時刻$t=t_0$の(初期)状態を$\rho_{t_0}=| \psi_{t_0} \rangle \langle \psi_{t_0}|
\in {\frak S}^p({\mathcal C}(H)^*)$
としよう.
時刻$t ( \ge t_0 )$での粒子$P$の状態
$\rho_t =
| \psi_{t} \rangle \langle \psi_{t}|$
とする.
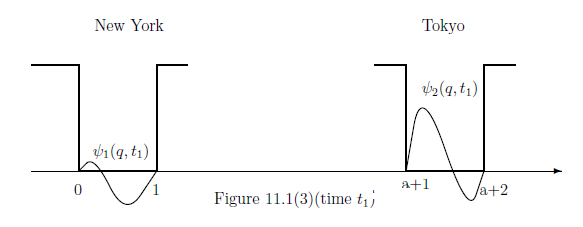
次に,二つの箱$[0,1]$
と
$[1,2]$を切り離して,$[1,2]$を遠く離れた$T$地点
(ニューヨーク)
に持って行き,これを
$[a,a+1]$とする.
ここで,
$|a|$はかなり大きいとする.
シュレーディンガー方程式(11.10)
を解いて
\begin{align*}
\psi_1(\cdot , t_1) +\psi_2(\cdot , t_1)
=
U_{t_0,t_1}\psi_{t_0}
\end{align*}
と置く。
ここに、
$U_{t_0,t_1}: L^2({\mathbb R}_{t_1}) \to L^2({\mathbb R}_{t_0})$
はユニタリ作用素となる。
因果作用素
$\Phi_{t_0, t_1}:
B(L^2({\mathbb R}_{t_2}))
\to
B(L^2({\mathbb R}_{t_1}))$
は次のように定まる:
\begin{align*}
\Phi_{t_0, t_1}(A)
=
U_{t_0,t_1}^* A U_{t_0,t_1}
\qquad
(\forall A \in B(L^2({\mathbb R}_{t_2})))
\end{align*}
さて,
$B(L^2({\mathbb R}, dq ))$内の観測量
${\mathsf O}=(X=\{N,T,E\}, 2^X, F )$
を次のように定義する.
\begin{align*}
&
[F(\{N\})](q)
=
\begin{cases}
1 \qquad & (q \in [0, 1] )
\\
0 \qquad & (それ以外 )
\end{cases}
\\
&
[F(\{T\})](q)
=
\begin{cases}
1 \qquad & (q \in [a, a+1] )
\\
0 \qquad & (それ以外 )
\end{cases}
\\
&
[F(\{ E \})](q)
=
1 -[F(\{N\})](q) -[F(\{T\})](q)
\end{align*}
注意11.7
上で、
測定値"N"
を得たと仮定しよう。
すなわち、
箱$[0,1]$内に電子を発見したとしよう。
このとき、
波動関数$\psi_2$
が消滅したと考えるかもしれない。
すなわち、
また、
ニューヨーク $\bigl[$resp. 東京$\bigl]$
を
地球
$\bigl[$resp. 北極星$\bigl]$
と考えてもよいわけで、
${\mathbf q}=(q_1, q_2, q_3 ) \in {\mathbb R}^3 $として,
\begin{align*}
\nabla^2
=
\frac{\partial^2}{\partial q_1^2}
+
\frac{\partial^2}{\partial q_2^2}
+
\frac{\partial^2}{\partial q_3^2}
\end{align*}
と定めて,
一粒子系のシュレーディンガー方程式:
\begin{align}
i \hbar \frac{\partial}{\partial t} \psi ( {\mathbf q}, t )
=
\Big[
\frac{- \hbar^2}{2m} \nabla^2 + V( {\mathbf q}, t )
\Big]
\psi ( {\mathbf q}, t )
\tag{11.9}
\end{align}
11.3:ド・ブロイのパラドックス(非局所性=超光速)
 シュレーディンガー方程式11.5 [Schrödinger equation in $\S$10.4.3]
シュレーディンガー方程式11.5 [Schrödinger equation in $\S$10.4.3]
ここに,
$\psi_t =\psi(\cdot , t ) \in H = L^2({\mathbb R}, dq)$は次の
シュレーディンガー方程式を満たす.
\begin{align}
\begin{cases}
初期条件:
\psi (\cdot , t_0 ) = \psi_{t_0}
\\
\\
i \hbar \frac{\partial}{\partial t} \psi ( { q}, t )
=
\Big[
\frac{- \hbar^2}{2m} \frac{\partial^2}{\partial q^2 } + V( {q}, t )
\Big]
\psi ( { q}, t )
\end{cases}
\tag{11.10}
\end{align}
ここで,
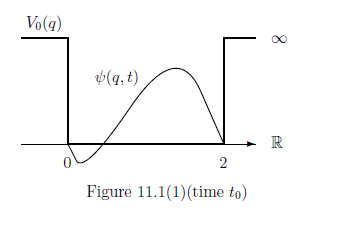
ポテンシャル$V(q,t)$は,以下のように定める.
$t=t_0$では,
\begin{align*}
V(q, t_0)=V_0(q)=\begin{cases}
0 \qquad & (0 \le q \le 2 )
\\
\infty &
(それ以外)
\end{cases}
\end{align*}で以下の通り:
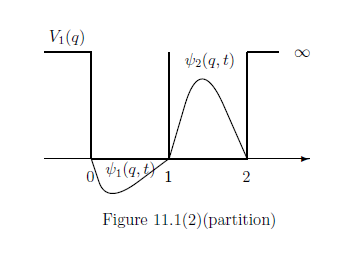
次に,
箱$[0,2]$の中に仕切り板を置いて,
二つの箱
$[0,1]]$
と
$[1,2]$
に分割する.
これは,
ポテンシャル
$V(,t)$を
$V_0 (q) $
から
$V_1 (q) $
に変化させることと同じである.
ここに,
ハイゼンベルグ描像で書けば
言語ルール1( 測定: $\S$2.7)
によって、
また、
シュレーディンガー描像で書けば
言語ルール1( 測定: $\S$2.7)
によって、
$(A_1):$
測定
$
{\mathsf M}_{B(L^2({\mathbb R}_{t_0}))}
\Big(
\Phi_{t_0,t_1}{\mathsf O},
S_{[|\psi_{t_0} \rangle \langle \psi_{t_0}|]}
\Big)
$
によって、
測定値
$
\left[\begin{array}{ll}
N
\\
T
\\
E
\end{array}\right]
$
が得られる確率は、
次で与えられる。
\begin{align*}
\left[\begin{array}{ll}
\langle u_{t_0} , \Phi_{t_0. t_1} F(\{N\}) u_{t_0} \rangle=
\int_0^1 |\psi_1(q , t_1)|^2 dq
\\
\langle u_{t_0} , \Phi_{t_0. t_1} F(\{T\})u_{t_0} \rangle
=
\int_{a+1}^{a+2} |\psi_2(q , t_1)|^2 dq
\\
\langle u_{t_0} , \Phi_{t_0. t_1} F(\{E \})u_{t_0} \rangle
=
0
\end{array}\right]
\end{align*}
ここで、当然のことであるが、
\begin{align*}
\mbox{(A$_1$)=(A$_2$)}
\end{align*}
であることに注意せよ。
$(A_2):$
測定
$
{\mathsf M}_{B(L^2({\mathbb R}_{t_0}))}
\Big(
{\mathsf O},
S_{[\Phi_{t_0,t_1}^*(|\psi_{t_0} \rangle \langle \psi_{t_0}|)]}
\Big)
$
によって、
測定値
$
\left[\begin{array}{ll}
N
\\
T
\\
E
\end{array}\right]
$
が得られる確率は、
次で与えられる。
\begin{align*}
\left[\begin{array}{ll}
\mbox{Tr} \Big(
\Phi_{t_0,t_1}^*(|\psi_{t_0} \rangle \langle \psi_{t_0}|) \cdot F(\{N\})
\Big)
=
\langle U_{t_0,t_1} \psi_{t_0} , F(\{N\}) U_{t_0,t_1} \psi_{t_0} \rangle
=
\int_0^1 |\psi_1(q , t_1)|^2 dq
\\
\mbox{Tr} \Big(
\Phi_{t_0,t_1}^*(|\psi_{t_0} \rangle \langle \psi_{t_0}|) \cdot F(\{T\})
\Big)
=
\langle U_{t_0,t_1} \psi_{t_0} , F(\{T\}) U_{t_0,t_1} \psi_{t_0} \rangle
=
\int_{a+1}^{a+2} |\psi_2(q , t_1)|^2 dq
\\
\mbox{Tr} \Big(
\Phi_{t_0,t_1}^*(|\psi_{t_0} \rangle \langle \psi_{t_0}|) \cdot F(\{E\})
\Big)
=
\langle U_{t_0,t_1} \psi_{t_0} , F(\{E\}) U_{t_0,t_1} \psi_{t_0} \rangle
=
0
\end{array}\right]
\end{align*}
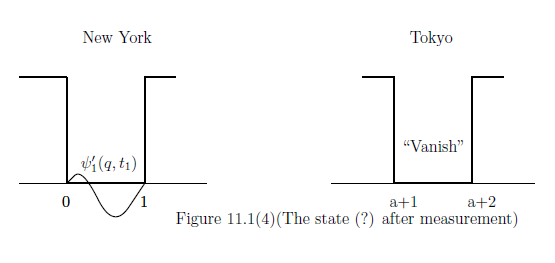
ここで、
$$
\psi'_1(q,t_1)= \frac{\psi_1(q,t_1)}{\| \psi'_1(\cdot ,t_1)\|}
$$
これは、次のような"波動関数の収縮(=測定後の状態)"
\begin{align}
\psi_1(\cdot, t_1)
+
\psi_2(\cdot, t_1)
\xrightarrow[\mbox{波動関数の収縮(=測定後の状態)}]{}
\psi'_1(\cdot,t_1)
\tag{11.12}
\end{align}
と呼ばれる「現象」である。
しかしながら、量子言語では、「状態は不変」のはずで、
したがって、
"波動関数の収縮(=測定後の状態)"は考えない。
この意味では、
$\bullet$
ハイゼンベルグ描像(A$_1$)だけに徹した方が間違えにくい
これは
" ド・ブロイのパラドックス"
と呼ばれる.
これは正真正銘のパラドックスで、
量子言語でも解決できるわけではない。
$\bullet$
結論11.6(($A_1)$でも$(A_2)$でも)は、「光より速い何かが存在する」ことを示唆している
11.3:ド・ブロイのパラドックス(非局所性=超光速)
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
結論11.6
