3.3.2: State does not move and quasi-product observable

"only one measurement" $\Longrightarrow$"state does not move" or "state is unchangeable"
That is because
$(a):$ In order to see the state movement, we have to take measurement at least more than twice. However, the "plural measurement" is prohibited. Thus, we conclude "state does not move"
Hence,
quantum laguage accepts Parmenides, and rejects Herakleitos







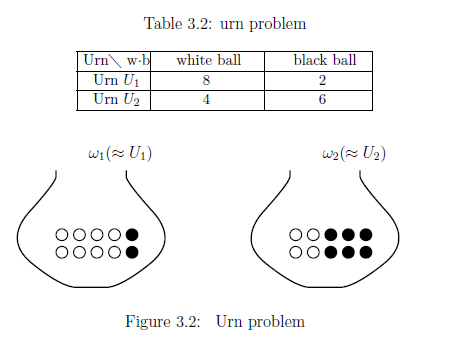
Review 3.16 [= Example 2.34] There are two urns ${U}_1$ and ${U}_2$. The urn ${U}_1$ [resp. ${U}_2$] contains 8 white and 2 black balls [resp. 4 white and 6 black balls] (cf. Figure 3.2).

Here, consider the following statement(a):
$(a):$ When one ball is picked up from the urn $U_2$, the probability that the ball is white is $0.4$.
In measurement theory, the statement (a) is formulated as follows: Assuming \begin{align} U_1 \quad \cdots \quad & \mbox{"the urn with the state $\omega_1 $"} \\ U_2 \quad \cdots \quad & \mbox{"the urn with the state $\omega_2 $"} \end{align}

define the state space $\Omega$ by $\Omega = \{ {\omega}_1 , {\omega}_2 \}$ with discrete metric and counting measure $\nu$. That is, we assume the identification;

\begin{align} U_1 \approx \omega_1, \quad U_2 \approx \omega_2, \quad \end{align} Thus, consider the classical basic structure: \begin{align} \mbox{{ $[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]$} } \end{align}

Put "$w$" = "white"$\!\!,\;$ "$b$" = "black"$\!\!\;$, and put $X=\{w,b\}$. And define the observable ${\mathsf O}_{{w}{b}} \big(\equiv (X \equiv \{w,b\}, 2^{\{w,b\}}, F_{{w}{b}}) \big)$ in $L^\infty (\Omega)$ by

\begin{align} [F_{{w}{b}}(\{w\})](\omega_1) = 0.8,& \qquad \qquad [F_{{w}{b}}(\{b\})](\omega_1) = 0.2, \nonumber \\ {}[F_{{w}{b}}(\{w\})](\omega_2) = 0.4,& \qquad \qquad [F_{{w}{b}}(\{b\})](\omega_2) = 0.6. \tag{3.13} \end{align}

Thus, we get the measurement $ {\mathsf M}_{L^\infty ({}\Omega{})} ({}{\mathsf O}_{{w}{b}} , S_{[{} \delta_{\omega_2}]})$. Here, Axiom 1 ( $\S$2.7)} says that

$(b):$ the probability that a measured value ${w}$ is obtained by ${\mathsf M}_{L^\infty ({}\Omega{})} ({}{\mathsf O}_{{w}{b}} , S_{[{} \delta_{\omega_2}]})$ is given by \begin{align} F_{{w}{b}}(\{b\})(\omega_2) = 0.4 \end{align}

Thus, the above statement (b) can be rewritten in the terms of quantum language as follows.

$(c):$ the probability that a measured value $ \left[\begin{array}{ll} {w} \\ {b} \end{array}\right] $ is obtained by the measurement ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{{w}{b}} ,$ $ S_{ [{}{\omega_2}]}{})$ is given by $\qquad \qquad \qquad \left[\begin{array}{ll} \int_\Omega [F_{{w}{b}}(\{{w}\})](\omega) \delta_{\omega_2}(d \omega ) = [F_{{w}{b}}(\{{w}\})](\omega_2)= 0.4 \\ \int_\Omega [F_{{w}{b}}(\{{b}\})](\omega) \delta_{\omega_2}(d \omega ) = {[F_{{w}{b}}(\{{b} \})]} (\omega_2)= 0.6 \end{array}\right] $
Problem 3.17 [Sampling with replacement]:
${}$ Pick out one ball from the urn $U_2$, and recognize the color ("white" or "black") of the ball. And the ball is returned to the urn. And again, Pick out one ball from the urn $U_2$, and recognize the color of the ball. Therefore, we have four possibilities such that. \begin{align} ({w},{w})\;\;({w},{b})\;\;({b},{w})\;\;({b},{b})\;\; \end{align} It is a common sense that \begin{align} \mbox{the probability that} \left[\begin{array}{ll} ({w},{w}) \\ ({w},{b}) \\ ({b},{w}) \\ ({b},{b}) \end{array}\right] \mbox{ is given by } \left[\begin{array}{ll} 0.16 \\ 0.24 \\ 0.24 \\ 0.36 \\ \end{array}\right] \end{align}
Now, we have the following problem:
$(a):$ How do we describe the above fact in term of quantum language?

Answer It suffices to consider the simultaneous measurement ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}^2_{{w}{b}} , S_{ [{}{\delta_{\omega_2}}]}{})$ (= ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{{w}{b}} \times {\mathsf O}_{{w}{b}} , S_{ [{}{\delta_{\omega_2}}]}{})$ ), where ${\mathsf O}_{{w}{b}}^2 = ( \{ {w}, {b} \}\times \{ {w}, {b} \} , 2^{\{ {w}, {b} \} \times \{ {w}, {b} \} } ,$ $ F_{{w}{b}}^2{}(= F_{{w}{b}} \times F_{{w}{b}} ) )$. Then, we calculate as follows.

\begin{align} & F_{{w}{b}}^2(\{ ({w}, {w}) \}{})(\omega_1{})= 0.64, \qquad F_{{w}{b}}^2(\{ ({w},{b}) \}{})(\omega_1{})= 0.16 \\ & F_{{w}{b}}^2(\{ ({b},{w}) \}{})(\omega_1{})= 0.16, \qquad F_{{w}{b}}^2(\{ ({b},{b}) \}{})(\omega_1{})= 0.4 \end{align} \begin{align} & F_{{w}{b}}^2(\{ ({w}, {w}) \}{})(\omega_2{})= 0.16, \qquad F_{{w}{b}}^2(\{ ({w},{b}) \}{})(\omega_2{})= 0.24 \\ & F_{{w}{b}}^2(\{ ({b},{w}) \}{})(\omega_2{})= 0.24, \qquad F_{{w}{b}}^2(\{ ({b},{b}) \}{})(\omega_2{})= 0.36 \end{align} Thus, we conclude that
$(b):$ the probability that a measured value $ \left[\begin{array}{ll} ({w},{w}) \\ ({w},{b}) \\ ({b},{w}) \\ ({b},{b}) \end{array}\right] $ is obtained by ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{{w}{b}} \times {\mathsf O}_{{w}{b}} , S_{ [{}{\delta_{\omega_2}}]}{})$
is given by $ \left[\begin{array}{llll} {[F_{{w}{b}}(\{{w}\})](\omega_2) \cdot [F_{{w}{b}}(\{{w}\})](\omega_2)=0.16} \\ {[F_{{w}{b}}(\{{w}\})](\omega_2) \cdot [F_{{w}{b}}(\{{b}\})](\omega_2)=0.24} \\ {[F_{{w}{b}}(\{{b}\})](\omega_2) \cdot [F_{{w}{b}}(\{{w}\})](\omega_2)=0.24} \\ {[F_{{w}{b}}(\{{b}\})](\omega_2) \cdot [F_{{w}{b}}(\{{b}\})](\omega_2)=0.36} \end{array}\right] $
$\square \quad$
Problem 3.18 [Sampling without replacement]:
${}$ Pick out one ball from the urn $U_2$, and recognize the color ("white" or "black") of the ball. And the ball is not returned to the urn. And again, pick out one ball from the urn $U_2$, and recognize the color of the ball. Therefore, we have four possibilities such that. \begin{align} ({w},{w})\;\;({w},{b})\;\;({b},{w})\;\;({b},{b})\;\; \end{align} It is a common sense that \begin{align} \mbox{the probability that} \left[\begin{array}{ll} ({w},{w}) \\ ({w},{b}) \\ ({b},{w}) \\ ({b},{b}) \end{array}\right] \mbox{ is given by } \left[\begin{array}{ll} {12}/{90} \\ {24}/{90} \\ {24}/{90} \\ {30}/{90} \\ \end{array}\right] \end{align}

Now, we have the following problem:

$(a):$ How do we describe the above fact in term of quantum language?

Now, recall the simultaneous observable (Definition 3.12) as follows. Let ${\mathsf O}_k$ ${{=}}$ $(X_k , $ ${\cal F}_k , $ $F_k{})$ ($k = 1,2,\ldots, n$ ) be observables in $\overline{\mathcal A}$. The simultaneous observable $\widehat{\mathsf O}$ ${{=}}$ $(\times_{k=1}^n X_k ,$　$ \boxtimes_{k=1}^n{\cal F}_k , $　$\widehat{F}{})$　is defined by

\begin{align} {\widehat F}(\Xi_1 \times \Xi_2 \times \cdots \times \Xi_n{}) = F_1 (\Xi_1{}) F_2 (\Xi_2{}) \cdots F_n (\Xi_n{}) \\ (\forall \Xi_k \in {\cal F}_k , \forall k =1,2,\ldots,n ) \end{align} The following definition　("quasi-product observable")　is a kind of simultaneous observable:

Definition　3.19 [quasi-product{ observable ] Let ${\mathsf O}_k$ ${{=}}$ $(X_k , $ ${\cal F}_k , $ $F_k{})$ ($k = 1,2,\ldots, n$ ) be observables in a $W^*$-algebra $\overline{\mathcal A}$. Assume that an observable ${\mathsf O}_{12...n}$ ${{=}}$ $(\times_{k=1}^n X_k ,$ $ \boxtimes_{k=1}^n{\cal F}_k , $ ${F}_{12...n}{})$ satisfies

\begin{align} & {F}_{12...n}(X_1 \times \cdots \times X_{k-1} \times \Xi_k \times X_{k+1} \times \cdots \times X_n ) = F_k (\Xi_k{}) \tag{3.14} \\ & \quad \qquad \qquad (\forall \Xi_k \in {\cal F}_k , \forall k =1,2,\ldots,n ) \end{align}

The observable ${\mathsf O}_{12...n}$ ${{=}}$ $(\times_{k=1}^n X_k ,$ $ \boxtimes_{k=1}^n{\cal F}_k , $ ${F}_{12...n}{})$ is called a quasi-product{ observable of $\{ {\mathsf O}_k \; | \;k=1,2,\ldots,n \}$, and denoted by

\begin{align} {\mathop{\overset{qp}{\times}}_{k=1,2,\ldots,n}}{\mathsf O}_k = (\times_{k=1}^n X_k , \boxtimes_{k=1}^n{\cal F}_k, {\mathop{\overset{qp}{\times}}_{k=1,2,\ldots,n} }F_k{}) \end{align}

Of course, a simultaneous observable is a kind of quasi-product observable. Therefore, quasi-product observable is not uniquely determined. Also, in quantum systems, the existence of the quasi-product observable is not always guaranteed.

Answer 3.20 [The answer to Problem 3.18]Define the quasi-product observable $ {\mathsf O}_{{w}{b}} \mathop{\overset{qp}{\times}} {\mathsf O}_{{w}{b}} = ( \{ {w}, {b} \} \times \{ {w}, {b} \} , 2^{\{ {w}, {b} \} \times \{ {w}, {b} \} } ,$ $ F_{12}(= F_{{w}{b}} \mathop{\overset{qp}{\times}} F_{{w}{b}} ))$ of ${\mathsf O}_{{w}{b}} = ( \{ {w}, {b} \}, 2^{\{ {w}, {b} \} } , F{})$ in $L^\infty (\Omega{})$ such that

\begin{align} & F_{12}(\{ ({w}, {w}) \}{})(\omega_1{})= \frac{8 \times 7}{90}, \qquad F_{12}(\{ ({w},{b}) \}{})(\omega_1{})= \frac{8 \times 2}{90} \\ & F_{12}(\{ ({b},{w}) \}{})(\omega_1{})= \frac{2 \times 8}{90}, \qquad F_{12}(\{ ({b},{b}) \}{})(\omega_1{})= \frac{2 \times 1}{90} \\ & F_{12}(\{ ({w}, {w}) \}{})(\omega_2{})= \frac{4 \times 3}{90}, \qquad F_{12}(\{ ({w},{b}) \}{})(\omega_2{})= \frac{4 \times 6}{90} \\ & F_{12}(\{ ({b},{w}) \}{})(\omega_2{})= \frac{6 \times 4}{90}, \qquad F_{12}(\{ ({b},{b}) \}{})(\omega_2{})= \frac{6 \times 5}{90} \end{align}

Thus, we have the (quasi-product) measurement ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{12}, S_{ [{}{\omega}]}{})$ Therefore, in terms of quantum language, we describe as follows.

$(b):$ the probability that a measured value $ \left[\begin{array}{ll} ({w},{w}) \\ ({w},{b}) \\ ({b},{w}) \\ ({b},{b}) \end{array}\right] $ is obtained dy ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{{w}{b}} \mathop{\overset{qp}{\times}} {\mathsf O}_{{w}{b}} , S_{ [{}{\delta_{\omega_2}}]}{})$
is given by $ \left[\begin{array}{lll} {[F_{12}(\{ ({w}, {w}) \})](\omega_2) =\frac{4 \times 3}{90} } \\ \\ { [F_{12}(\{({w}, {b})\})](\omega_2) =\frac{4 \times 6}{90} } \\ \\ { [ F_{12}(\{ ({b}, {w}) \})](\omega_2) =\frac{4 \times 6}{90} } \\ \\ { [F_{12}(\{({b}, {b}) \}{})](\omega_2) =\frac{6 \times 5}{90} } \end{array}\right] $
$\square \quad$