The argument in $\S4.3$ is due to refs [1, 8] in $\S$0.0 (my home page).


4.3.1: Heisenberg's uncertainty principle is doubtful
Heisenberg's uncertainty principle is as follows.
　Proposition 4.10 [Heisenberg's uncertainty principle]
$\mbox{(i):}$ 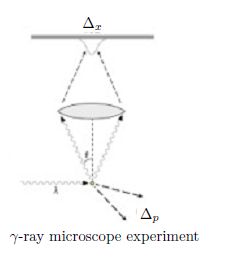The position $x$ of a particle $P$ can be measured exactly. Also similarly, the momentum $p$ of a particle $P$ can be measured exactly. However, the position $x$ and momentum $p$ of a particle $P$ can not be measured simultaneously and exactly, namely, the both errors $\Delta_x$ and $\Delta_p$ can not be equal to $0$. That is, the position $x$ and momentum $p$ of a particle $P$ can be measured simultaneously and approximately,
(ii): And, $\Delta_x$ and $\Delta_p$ satisfy Heisenberg's uncertainty principle as follows. \begin{align} \Delta_x \cdot \Delta_p \; {\doteqdot} \; \hbar (= \mbox{Plank constant}/2\pi {\doteqdot} 1.5547 \times 10^{-34} Js ). \tag{4.20} \end{align}

This was discovered by Heisenberg's thought experiment due to $\gamma$-ray microscope. It is

$(A):$ one of the most famous statements in the 20-th century.
But, we think that it is doubtful in the following sense.
$\fbox{Note 4.1}$I think that Heisenberg's uncertainty principle(Proposition 4.10) is meaningless. That is because, for example,
$(\sharp):$ The approximate measurement and "error" in Proposition 4.10 are not defined.

This will be improved in Theorem 4.15 (in $\S$4.3.3) in the framework of quantum mechanics. That is, Heisenberg's thought experimentis an excellent idea before the discovery of quantum mechanics. Some may ask that

$(\sharp):$ If it be so, why is Heisenberg's uncertainty principle (Proposition 4.10) famous?
I think that
$(\sharp):$ Heisenberg's uncertainty principle (Proposition 4.10) was used as the slogan for advertisement of quantum mechanics in order to emphasize the difference between classical mechanics and quantum mechanics.

And, this slogan was completely successful. This kind of slogan is not rare in the history of science. For example, recall "cogito proposition (due to Descartes)", that is,

\begin{align} \mbox{ I think, therefore I am. } \end{align}

which is also meaningless (cf. $\S$8.4). However, it is certain that the cogito proposition built the foundation of modern science.

$\fbox{Note 4.2}$ Heisenberg's uncertainty principle (Proposition 4.10) may include contradiction, if we think as follows
$(\sharp):$ it is "natural" to consider that \begin{align} \Delta_x = | x - \widetilde{x}|, \quad \Delta_p = | p - \widetilde{p}|, \end{align} where \begin{align} \left\{\begin{array}{ll} \mbox{Position:}\quad & [x:\mbox{exact measured value (=true value)}, \widetilde{x}: \mbox{measured value}] \\ \mbox{Momentum:}\quad & [p:\mbox{exact measured value (=true value)}, \widetilde{p}: \mbox{measured value}] \end{array}\right. \end{align}
However, this is in contradiction with Heisenberg's uncertainty principle (4.20). That is because (4.20) says that the exact measured value $(x, p)$ can not be measured.