$\S$4.4.1: EPR-paradox

Let us explain EPR-paradox (Einstein--Poolside--Rosen). Consider Two electrons $P_1$ and $P_2$ and their spins. Thetensor Hilbert space $H={\mathbb C}^2 \otimes {\mathbb C}^2$ is defined in what follows. That is,

\begin{align} e_1= \left[\begin{array}{l} 1 \\ 0 \end{array}\right], \quad e_2 = \left[\begin{array}{l} 0 \\ 1 \end{array}\right] \end{align} (i.e., the complete orthonormal system $\{ e_1, e_2 \}$ in the ${\mathbb C}^2$), \begin{align} {\mathbb C}^2 \otimes {\mathbb C}^2 = \{ \sum\limits_{i,j=1,2} \alpha_{ij} e_i \otimes e_j \;|\; \alpha_{ij} \in {\mathbb C}, i,j=1,2 \} \end{align}

Put $u=\sum\limits_{i,j=1,2} \alpha_{ij} e_i \otimes e_j$ and $v=\sum\limits_{i,j=1,2} \beta_{ij} e_i \otimes e_j$. And the inner product $\langle u,v \rangle_{_{{\mathbb C}^2 \otimes {\mathbb C}^2}}$ is defined by

\begin{align} \langle u,v \rangle_{_{{\mathbb C}^2 \otimes {\mathbb C}^2}} = \sum\limits_{i,j=1,2} \overline{\alpha}_{i,j}\cdot \beta_{i,j} \end{align}

Therefore, we have the tensor Hilbert space $H={\mathbb C}^2 \otimes {\mathbb C}^2$ with the complete orthonormal system $\{ e_1 \otimes e_1, e_1 \otimes e_2, e_2 \otimes e_1, e_2 \otimes e_2 \}$. For each $F\in B({\mathbb C}^2)$ and $G\in B({\mathbb C}^2)$, define the $F\otimes G \in B({\mathbb C}^2 \otimes {\mathbb C}^2)$ (i.e., linear operator $F\otimes G : {\mathbb C}^2 \otimes {\mathbb C}^2 \to {\mathbb C}^2 \otimes {\mathbb C}^2$ ) such that

\begin{align} (F \otimes G) ( u \otimes v) = Fu \otimes Gv \end{align}

Let us define the entangled state $ \rho = |s \rangle \langle s | $ of two particles $P_1$ and $P_2$ such that

\begin{align} s= \frac{1}{\sqrt 2} (e_1\otimes e_2 - e_2 \otimes e_1 ) \end{align}

Here, we see that $\langle s,s \rangle_{_{{\mathbb C}^2 \otimes {\mathbb C}^2}}$ $=\frac{1}{2}\langle e_1\otimes e_2 - e_2 \otimes e_1 ,e_1\otimes e_2 - e_2 \otimes e_1 \rangle_{_{{\mathbb C}^2 \otimes {\mathbb C}^2}}$ $=\frac{1}{2}(1+1)=1$, and thus, $\rho$ is a state. Also, assume that

two particles $P_1$ and $P_2$ are far.

Let ${\mathsf O} =(X,2^X, F^z )$ in $B({\mathbb C}^2)$ (where $X=\{\uparrow ,\downarrow \}$ ) be the spin observable concerning the $z$-axis such that

\begin{align} F^z( \{ \uparrow \}) = \left[\begin{array}{lL} 1 & 0 \\ 0 & 0 \end{array}\right] \quad F^z( \{ \downarrow \}) = \left[\begin{array}{ll} 0 & 0 \\ 0 & 1 \end{array}\right] \end{align}

The parallel observable ${\mathsf O}\otimes {\mathsf O} =(X^2,2^X\times 2^X, F^z \otimes F^z)$ in $B({\mathbb C}^2\otimes {\mathbb C}^2)$ is defined by

\begin{align} & (F^z \otimes F^z)(\{(\uparrow,\uparrow )\})=F^z(\{\uparrow \}) \otimes F^z(\{\uparrow \}) = \left[\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right] \otimes \left[\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right] \;\; \\ & (F^z \otimes F^z)(\{(\downarrow,\uparrow )\})=F^z(\{\downarrow \}) \otimes F^z(\{\uparrow \}) = \left[\begin{array}{ll} 0 & 0 \\ 0 & 1 \end{array}\right] \otimes \left[\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right] \\ & (F^z \otimes F^z)(\{(\uparrow,\downarrow )\})=F^z(\{\uparrow \}) \otimes F^z(\{\downarrow \}) = \left[\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right] \otimes \left[\begin{array}{ll} 0 & 0 \\ 0 & 1 \end{array}\right] \;\;\\ & (F^z \otimes F^z)(\{(\downarrow,\downarrow )\})=F^z(\{\downarrow \}) \otimes F^z(\{\downarrow \}) = \left[\begin{array}{ll} 0 & 0 \\ 0 & 1 \end{array}\right] \otimes \left[\begin{array}{ll} 0 & 0 \\ 0 & 1 \end{array}\right] \end{align}

Thus, we get the measurement ${\mathsf M}_{B({\mathbb C}^2\otimes {\mathbb C}^2)}({\mathsf O}\otimes {\mathsf O},S_{[\rho]})$ Then, Born's quantum measurement theory says that

$\bullet$ When the parallel measurement ${\mathsf M}_{B({\mathbb C}^2\otimes {\mathbb C}^2)}({\mathsf O}\otimes {\mathsf O},S_{[s]})$ is taken,
the probability that the measured value $ \left[\begin{array}{ll} (\uparrow,\uparrow ) \\ (\downarrow,\uparrow ) \\ (\uparrow,\downarrow ) \\ (\downarrow,\downarrow ) \end{array}\right] $ is obtained is given by \begin{align} \left[\begin{array}{ll} \langle s, (F^z \otimes F^z)(\{(\uparrow,\uparrow )\})s \rangle_{_{{\mathbb C}^2 \otimes {\mathbb C}^2}} = 0 \\ \langle s, (F^z \otimes F^z)(\{(\downarrow,\uparrow )\})s \rangle_{_{{\mathbb C}^2 \otimes {\mathbb C}^2}} = 0.5 \\ \langle s, (F^z \otimes F^z)(\{(\uparrow,\downarrow )\})s \rangle_{_{{\mathbb C}^2 \otimes {\mathbb C}^2}} = 0.5 \\ \langle s, (F^z \otimes F^z)(\{(\downarrow,\downarrow )\})s \rangle_{_{{\mathbb C}^2 \otimes {\mathbb C}^2}} = 0 \end{array}\right] \tag{4.46} \end{align}

That is because, $F^z (\{\uparrow \})e_1=e_1$, $F^z (\{\downarrow \})e_2=e_2,F^z (\{\uparrow \})e_2= F^z (\{\downarrow \})e_1=0$ For example,

\begin{align} & \langle s, (F^z \otimes F^z)(\{(\uparrow,\downarrow )\})s \rangle_{_{{\mathbb C}^2 \otimes {\mathbb C}^2}} \\ = & \frac{1}{2}\langle (e_1\otimes e_2 - e_2 \otimes e_1 ) , (F^z(\{\uparrow \}) \otimes F^z(\{\downarrow \}) (e_1\otimes e_2 - e_2 \otimes e_1 ) \rangle_{_{{\mathbb C}^2 \otimes {\mathbb C}^2}} \\ = & \frac{1}{2}\langle (e_1\otimes e_2 - e_2 \otimes e_1 ) , e_1\otimes e_2 \rangle_{_{{\mathbb C}^2 \otimes {\mathbb C}^2}} = \frac{1}{2} \end{align}

Here, it should be noted that we can assume that the $x_1$ and the $x_2$ (in $(x_1, x_2)$ $ \in $ $\{$ $ (\uparrow _{z},\uparrow _{z}),$ $ (\uparrow _{z},\downarrow _{z}),$ $ (\downarrow _{z},\uparrow _{z}), (\downarrow _{z},\downarrow _{z}) \}$) are respectively obtained in Tokyo and in New York (or, in the earth and in the polar star).

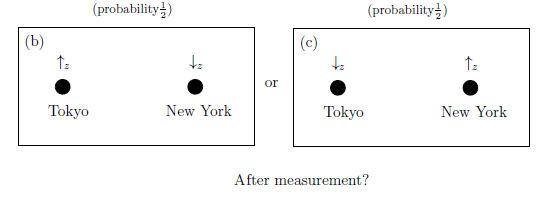
This fact is, figuratively speaking, explained as follows:
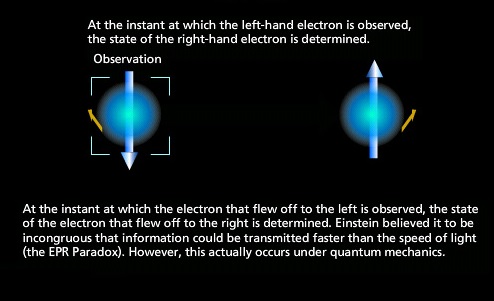
$\bullet$ Immediately after the particle (or, wavefunction) in Tokyo is measured and the measured value $\uparrow _{z}$ [resp. $\downarrow _{z}$] is observed, the particle (or, wavefunction) in Tokyo informs the particle (or, wavefunction) in New York " Your measured value has to be $\downarrow _{z}$ [resp. $\uparrow _{z}$]"$\!\!\!\!.\; \;$
Therefore, the above fact implies that quantum mechanics says that \begin{align} \mbox{there is something faster than light.} \end{align} This is essentially the same as the de Broglie paradox. That is,
$\bullet$ if we admit quantum mechanics, we must also admit the fact that there is
something faster than light (i.e., so called "non-locality").
$\fbox{Note 4.4}$ EPR-paradox is closely related to the fact that quantum syllogism does not hold in general. This will be discussed in Chapter 8. The Bohr-Einstein debates were a series of public disputes about quantum mechanics between Albert Einstein and Niels Bohr. Although Bohr may assert that his Copenhagen interpretation belongs to physics, I want to regard this debates as \begin{align} \underset{\mbox{ (realistic view)}}{\fbox{$\mbox{Einstein}$}} \quad \underset{\mbox{v.s.}}{\longleftrightarrow} \quad \underset{\mbox{ (linguistic view)}}{\fbox{$\mbox{Bohr}$}} \end{align} For the further argument, see Section 10.7 (Leibniz-Clarke debates). I want to believe that the grand debates in science should be always "realistic view vs. linguistic view".