This section is extracted from the following:
4.5.1: Bell's inequality is violated in both classical and quantum systems
Firstly, let us mention Bell's inequality in mathematics.
Define the measured value space $X^2=\{-1,1\}^2$ such that $X^2=\{-1,1\}^2
=
\{
(1,1),
(1,-1),
$ $
(-1,1),
$ $
(-1,-1)
\}$.
Consider two complex numbers $a= {\alpha}_1 +{\alpha}_2{}{\sqrt{-1}} $ and $b= {}{\beta}_1 +{\beta}_2{}{\sqrt{-1}}$ such that $| a |$ $\equiv$ $\sqrt{{}| \alpha_1 |^2 + | {\alpha}_2 |^2{}} =1$ and $| b |$ $\equiv$ $\sqrt{{}| \beta_1 |^2 + | {\beta}_2 |^2{}} =1$. Define the probability space $( X^2, {\cal P}(X^2), \nu_{ab})$ such that
For each $c \in \{a,b\}$, define the observable ${\mathsf O}_c$ $\equiv$ $\bigl(X ,{\cal P}(X) , G_c \bigl)$ in $B({\mathbb C}^2) $ such that
Consider the two particles quantum system in ${ B }({\mathbb C}^2 \otimes {\mathbb C}^2)$.
Consider two states $\rho_s$ $= | {\psi_s} \rangle \langle {\psi_s} |$ and $\rho_0$ $= | {\psi_0} \rangle \langle {\psi_0} |$ $\bigl(\in {\frak S}^p( { B }({\mathbb C}^2 \otimes {\mathbb C}^2)^*) \bigl)$. Here, put $\psi_s=(e_1\otimes e_2 -e_2\otimes e_1)/{\sqrt{2}}$ and $\psi_0=e_1\otimes e_1$.
Consider the unitary operator $U$ $( \in B({\mathbb C}^2 \otimes {\mathbb C}^2)$ such that $U\psi_0 =\psi_s$.
Consider an observable ${\mathsf O}_{ab} $ $=$ $(X^2 , {\cal P}(X^2) , F_{ab}:= U^* (G_a \otimes G_b)U )$ in $B({\mathbb C}^2 \otimes {\mathbb C}^2)$, and get the measurement ${\mathsf M}_{B({\mathbb C}^2 \otimes {\mathbb C}^2)} ({\mathsf O}_{ab} ,S_{[{}\rho_0{}]})$.
This clearly satisfies (D). That is because we see that, for each $(x_1,x_2) \in X^2$,
(ii): classical case: [${\cal A}=C_0(\Omega) \otimes C_0(\Omega)=C_0(\Omega \times \Omega)$]
Put $\omega_0 (=(\omega_0', \omega''_0)) \in \Omega \times \Omega$, and $\rho_0 = \delta_{\omega_0} $ ($\in {\frak S}^p ({C_0(\Omega \times \Omega)}^*)$).
Define the observable ${\mathsf O}_{ab}:=( X^2, {\cal P}(X^2), F_{ab})$ in $L^\infty (\Omega \times \Omega)$ such that
[1]: S. Ishikawa, “A New Interpretation of Quantum Mechanics,Journal of Quantum Information Science,” Vol. 1 No. 2, 2011, pp. 35-42. doi: 10.4236/jqis.2011.12005 ( download free)
Here, let us prepare three steps (I$\sim$III) as follows.
[Step I]: Consider the basic structure:
\begin{align}
[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]
\end{align}
${}$ Find the measurement ${\mathsf M}_{\overline {\mathcal A} } ({\mathsf O}_{ab}:=( X^2,$ $ {\cal P}(X^2),$ $ F_{ab}) ,$ $S_{[\rho_0]})$ that satisfies
\begin{align}
\nu_{ab} (\Xi)= \rho_0( F_{ab} (\Xi))
\;\;
\quad
(\forall \Xi \in {\cal P}(X^2))
\end{align}
[Step: II]: Consider the problem in the two cases. That is,
(i): quantum case [${\cal A}=B({\mathbb C}^2) \otimes B({\mathbb C}^2) =B({\mathbb C}^2 \otimes {\mathbb C}^2)$ ]
Put
\begin{align}
e_1=
\left[\begin{array}{l}
1
\\
0
\end{array}\right],
\quad
e_2=
\left[\begin{array}{l}
0
\\
1
\end{array}\right]
\quad
(\in {\mathbb C}^2 ).
\end{align}
${}$ $
\left\{\begin{array}{ll}
\mbox{(i):quantum case:
[${\cal A}=B({\mathbb C}^2 \otimes {\mathbb C}^2)$]
}
\\
\mbox{(ii):classical case:
[${\cal A}=C_0(\Omega \times \Omega)$]
}
\end{array}\right.
$
[Step III]:
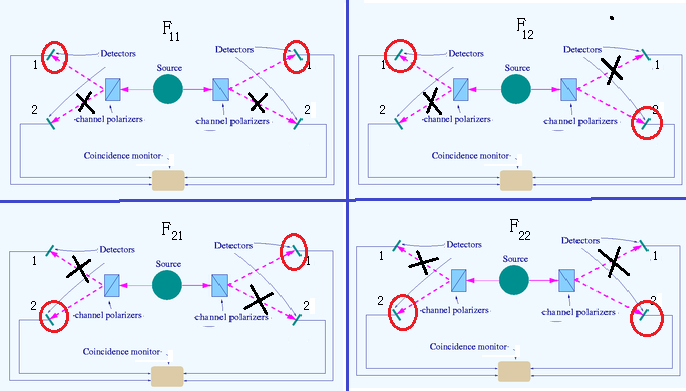
For each $k=1,2$, consider two complex numbers $a^k (=\alpha_1^k+\alpha_2^k{\sqrt{-1}} )$ and $b^k(=\beta_1^k+\beta_2^k{\sqrt{-1}})$ such that $| a^k |=| b^k |=1$. Consider the tensor parallel measurement $\otimes_{i,j=1,2}$ ${\mathsf M}_{ {\cal A} } ({\mathsf O}_{a^ib^j}:=( X^2, {\cal P}(X^2), F_{a^ib^j}) ,$ $S_{[\rho_0]})$ in the tensor $W^*$-algebra $ \otimes_{{}_{i,j=1,2}} \overline{\mathcal A} $. Assume the measured value $x (\in X^8)$. That is,
\begin{align} x & = \big( (x_{1}^{11} , x_{2}^{11}), (x_{1}^{12} , x_{2}^{12}), (x_{1}^{21} , x_{2}^{21}), (x_{1}^{22} , x_{2}^{22}) \big) \\ & \in \times_{i,j=1,2} X^2 \end{align} Here, we see, by (4.50), that, for any $i,j=1,2$, \begin{align} P({a^{i},b^{j}}) & = \!\!\! \sum_{(x^{ij}_1, x^{ij}_2) \in X\times X } \!\!\! x^{ij}_1 \cdot x^{ij}_2 \rho_0 (F_{a^ib^j}( \{(x^{ij}_1,x^{ij}_2)\} )) \\ & = -\alpha^{i}_1 \beta^{j}_1 - \alpha^{i}_2 \beta^{j}_2 \end{align} Putting \begin{align} a^1 ={\sqrt{-1}}, \; b^1 = \frac{1+{{\sqrt{-1}}}}{ \sqrt{2} }, \; a^2 = 1, \; b^2 = {}\frac{1-{{\sqrt{-1}}}}{ \sqrt{2} }, \end{align} we get the following equality: \begin{align} |P(a^1 , b^1) - P(a^1 , b^2)| \; + \; |P(a^2 , b^1) + P(a^2 , b^2 )| = 2 \sqrt{2} \tag{4.51} \end{align} Thus, in both cases ( i.e., quantum case [${\cal A}=B({\mathbb C}^2 \otimes {\mathbb C}^2)$] and classical case [${\cal A}=C_0(\Omega\times \Omega)$]), the formula (4.51) holds.This fact is often said that
4.5.2: Stop being bothered
 Remark 4.18 [Shut up and calculate]. The above argument may suggest that there is something faster than light. However, when faster-than-light appears, our standing point is
Remark 4.18 [Shut up and calculate]. The above argument may suggest that there is something faster than light. However, when faster-than-light appears, our standing point is
| $(a):$ | "Most physicists, I think it is fair to say, are not bothered." |
| (b): | If I were forced to sum up in one sentence what the Copenhagen interpretation says to me,
it would be "Shut up and calculate" |
| $(c):$ | If I were forced to sum up in one sentence what the linguistic interpretation says to me,
it would be "Shut up and calculate" |
