Abstract:
Measurement theory (= quantum language ) is formulated as follows.
\[
\underset{\mbox{ (=quantum language)}}{\fbox{pure measurement theory (A)}}
:=
\underbrace{
\underset{\mbox{ (\(\S\)2.7)}}{
\overset{
[\mbox{ (pure) Axiom 1}]
}{\fbox{pure measurement}}
}
+
\underset{\mbox{ ( \(\S \)10.3)}}{
\overset{
[{\mbox{ Axiom 2}}]
}{\fbox{Causality}}
}
}_{\mbox{ a kind of incantation (a priori judgment)}}
+
\underbrace{
\underset{\mbox{
(\(\S\)3.1)
}}
{
\overset{
{}}{\fbox{Linguistic interpretation}}
}
}_{\mbox{ the manual on how to use spells}}
\]
Measurement theory says that
In this chapter, we study Fisher statistics in terms of Axiom 1 ( measurement: $\S$2.7).
We shall emphasize
$\bullet$ Describe every phenomenon modeled on Axioms 1 and 2 (by a hint of the linguistic interpretation)!
The readers can read this chapter without the knowledge of statistics.
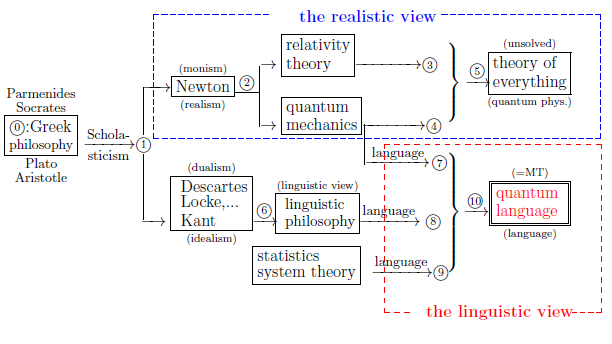
Again recall that, as mentioned in $\S$1.1, the main purpose of this book is to assert the following figure 1.1: