Abstract of Chap. 8
The term "practical logic" means the logic in measurement theory. It is certain that pure logic (=mathematical logic) is merely a kind of rule in mathematics (or meta-mathematics). If it is so, the mathematical logic is not guaranteed to be applicable to our world. For instance, mathematical syllogism ( "$A \Rightarrow B$" and "$B \Rightarrow C$" imply "$A \Rightarrow C$" ) does not assure the following famous statement:
| $(\sharp_1):$ | Since Socrates is a man and all men are mortal, it follows that Socrates is mortal.
|
That is, we think that
| $(\sharp_2):$ | the above ($\sharp_1 $) is not clarified yet.
|
In this chapter, we prove the $(\sharp_1)$ in classical systems. Also, we point out that syllogism does not hold
in quantum systems
This chapter is mostly extracted from
the following:
Again recall that, as mentioned in $\S$1.1, the main purpose of this book is to
assert the following figure 1.1:
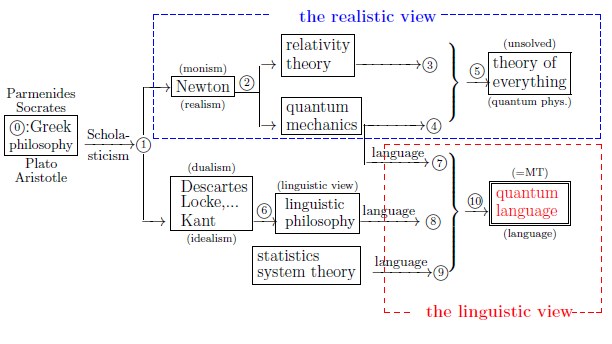Fig.1.1: the location of "quantum language" in the world-views
This(particularly, ⑦--⑨) implies that quantum language has the following three aspects:
$$
\left\{\begin{array}{ll}
\mbox{ ⑦ :the standard interpretation of quantum mechanics}
\\
\mbox{
$\qquad$
(i.e., the true colors of the Copenhagen interpretation)
}
\\
\\
\mbox{ ⑧ :
the final goal of the dualistic idealism (Descartes=Kant philosophy)
}
\\
\\
\mbox{ ⑨ :
theoretical statistics of the future
}
\end{array}\right.
$$
