8.5: Combined observable ---Only one measurement is permitted
The linguistic interpretation
says that
\begin{align}
&
\mbox{"Only one measurement is permitted"}
\\
&
\Rightarrow
\mbox{
"only one observable"}
\Rightarrow
\mbox{
"the necessity
of the combined observable"}
\end{align}
Thus, we prepare the following theorem.
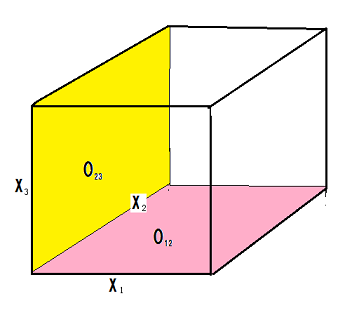Theorem8.9 [The existence theorem of classical combined observable]
Consider the classical basic structure
\begin{align}
[C_0(\Omega ) \subseteq L^\infty ( \Omega, \nu ) \subseteq B(L^2 ( \Omega, \nu ))]
\end{align}
And consider observables
${\mathsf O}_{12}{{=}} (X_1 \times X_2 , {\mathcal F}_1 \boxtimes {\mathcal F}_2, F_{12})$
and
${\mathsf O}_{23}{{=}} $
$(X_2 \times X_3 ,$
$ {\mathcal F}_2 \boxtimes {\mathcal F}_3, F_{23})$
in
$L^\infty ( \Omega, \nu )$.
Here, for simplicity,
assume that
$X_i{{=}} \{x^1_i, x^2_i,\ldots, x^{n_i}_i\}$
$(i=1,2,3)$
is finite,
Also,
assume that ${\mathcal F}_i = 2^{X_i}$.
Furthermore assume that
\begin{align}
{\mathsf O}_{12}^{(2)}
=
{\mathsf O}_{23}^{(2)}
\quad
(\mbox{That is, }\;\;
F_{12}(X_1 \times \Xi_2 )
=
F_{23}(\Xi_2 \times X_3 )
\quad(\forall \Xi_2 \in 2^{X_2}))
\end{align}
Then,
we have
the observable
${\mathsf O}_{123}{{=}} (X_1 \times X_2 \times X_3,
{\mathcal F}_1 \times {\mathcal F}_2 \times {\mathcal F}_3, F_{123})$
in $L^\infty (\Omega)$
such that
\begin{align}
{\mathsf O}_{123}^{(12)}
=
{\mathsf O}_{12},
\quad
{\mathsf O}_{123}^{(23)}
=
{\mathsf O}_{23}
\end{align}
That is,
\begin{align}
F_{123}^{(12)}(\Xi_1 \times \Xi_2 \times X_3)
&
=
F_{12}(\Xi_1 \times \Xi_2 ),\;\;
F_{123}^{(23)}(X_1 \times \Xi_2 \times \Xi_3 )
=
F_{23}(\Xi_2 \times \Xi_3 )
\tag{8.8}
\\
&
\quad(\forall \Xi_1 \in {\mathcal F}_1,
\forall \Xi_2 \in {\mathcal F}_2,
\forall \Xi_3 \in {\mathcal F}_3
))
\nonumber
\end{align}
The
${\mathsf O}_{123}$
is called the {combined observable of
${\mathsf O}_{12}$
and
${\mathsf O}_{23}$.
Proof.
${\mathsf O}_{123}$
$=$
$(X_1 \times X_2 \times X_{3} , $
${ {\mathcal F}_1 \times {\mathcal F}_{2} \times {\mathcal F}_3}, $
$F_{123})$
is, for example,
defined by
\begin{align}
&
\; \;
[{}F_{123}
(\{(x_{1} , x_{2} , x_{3}^{}) \})
]
(\omega)
\\
&
=
\left\{\begin{array}{ll}
{\displaystyle
\frac{
[{}F_{12} (\{(x_{1} , x_{2}) \}){}]
(\omega)
\cdot
[{}F_{23} (\{(x_{2} , x_{3}) \}){}]
(\omega)
}
{
[{}F_{12} (X_1 \times \{ x_{2} \}){}]
(\omega)
}
}
\\
& \hspace{-2cm}
(
[{}F_{12} (X_1 \times \{ x_{2} \}){}]
(\omega)
\;
\not= 0\mbox{ and })
\\
\\
0
\\
& \hspace{-2.0cm}
(
[{}F_{12} (X_1 \times \{ x_{2} \}){}]
(\omega)
= 0\mbox{ and })
\\
\end{array}\right.
\\
&
\qquad \qquad \qquad
(\forall \omega \in \Omega,
\forall
(x_1,x_2,x_3) \in X_1 \times X_2 \times X_3)
\end{align}
This clearly satisfies (8.8).
\qed
Counter example8.10 [Counter example in quantum systems]
Theorem 8.9Theorem does not hold
in
the
quantum basic structure
\begin{align}
[{\mathcal C}(H) \subseteq B(H) \subseteq B(H)]
\end{align}
For example,
put
$H={\mathbb C}^n$,
and
consider the three Hermitian $(n \times n)$-matrices
$T_1$, $T_2$, $T_3$
in
$B(H)$
such that
\begin{align}
T_1 T_2 =T_2 T_1, \quad T_2 T_3 =T_3 T_2, \quad
T_1 T_3 \not= T_3 T_1
\tag{8.9}
\end{align}
For each $k=1,2,3$,
define the spectrum decomposition
${\mathsf O}_k=(X_k, {\mathcal F}_k, F_k )$
in $H$
(which is regarded as a projective observable)
such that
\begin{align}
T_k = \int_{X_k} x_k F_k ( d x_k )
\tag{8.10}
\end{align}
where
$X_k ={\mathbb R}, {\mathcal F}_k={\mathcal B}_{\mathbb R}$.
From the commutativity,
we have the simultaneous observables
\begin{align}
&
{\mathsf O}_{12}{{=}} {\mathsf O}_1 \times {\mathsf O}_2 =(X_1 \times X_2 , {\mathcal F}_1 \boxtimes {\mathcal F}_2, F_{12}=F_1 \times F_2)
\nonumber
\end{align} \begin{align}
&
{\mathsf O}_{23}{{=}} {\mathsf O}_2 \times {\mathsf O}_3=
(X_2 \times X_3 , {\mathcal F}_2 \boxtimes {\mathcal F}_3, F_{23}=F_2 \times F_3)
\end{align}
It is clear that
\begin{align}
{\mathsf O}_{12}^{(2)}
=
{\mathsf O}_{23}^{(2)}
\quad
(\mbox{that is,}\;\;
F_{12}(X_1 \times \Xi_2 )
=F_2(\Xi_2 )
=
F_{23}(\Xi_2 \times X_3 )
\quad(\forall \Xi_2 \in {\mathcal F}_2))
\end{align}
However, it should be noted that
there does not exist the
observable
${\mathsf O}_{123}{{=}} (X_1 \times X_2 \times X_3,
{\mathcal F}_1 \boxtimes {\mathcal F}_2 \boxtimes {\mathcal F}_3, F_{123})$
in $B(H)$
such that
\begin{align}
{\mathsf O}_{123}^{(12)}
=
{\mathsf O}_{12},
\quad
{\mathsf O}_{123}^{(23)}
=
{\mathsf O}_{23}
\end{align}
That is because,
if
${\mathsf O}_{123}$
exists, Theorem 8.3Theorem says that
${\mathsf O}_1$
and ${\mathsf O}_3$
commute,
and it is in contradiction with the
(8.9).
Therefore,
the combined observable ${\mathsf O}_{123}$
of
${\mathsf O}_{12}$
and
${\mathsf O}_{23}$
does not exist.
8.5.2: Combined observable and Bell's inequality
Now we consider the following problem:
Problem 8.11 [combined observable and Bell's inequality]
Consider the basic structure
\begin{align}
[ {\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]
\end{align}
Put $X_1=X_2=X_3=X_4=\{-1, 1\}$.
Let
${\mathsf O}_{13}{{=}} (X_1 \times X_3 ,
2^{X_1} \times 2^{X_3} , F_{13})$,
${\mathsf O}_{14}{{=}} (X_1 \times X_4 ,
2^{X_1} \times
2^{X_4}
, F_{14})$,
${\mathsf O}_{23}{{=}} $
$(X_2 \times X_3 ,$
$ 2^{X_2} \times 2^{X_3} , F_{23})$
and
${\mathsf O}_{24}{{=}} $
$(X_2 \times X_3 ,$
$ 2^{X_2} \times 2^{X_4} , F_{24})$
be observables in
$L^\infty (\Omega)$
such that
\begin{align}
{\mathsf O}_{13}^{(1)}={\mathsf O}_{14}^{(1)},
\;\;
{\mathsf O}_{23}^{(2)}={\mathsf O}_{24}^{(2)},
\;\;
{\mathsf O}_{13}^{(3)}={\mathsf O}_{23}^{(3)},
\;\;
{\mathsf O}_{14}^{(4)}={\mathsf O}_{24}^{(4)}
\end{align}
Define the probability measure $\nu_{ab}$
on
$\{-1, 1 \}^2$
by
the formula (4.49).
Assume that
there exists
a state
$\rho_0 \in {\frak S}^p({\mathcal A}^*) $
such that
\begin{align}
&
{}_{{\mathcal A}^*} \big(\rho_0,
F_{13}(\{(x_1,x_3)\})
\big) {}_{\overline{\mathcal A} }
=\nu_{a^1b^1}(\{(x_1,x_3)\},
\\
&
{}_{{\mathcal A}^*} \big(\rho_0,
F_{14}(\{(x_1,x_4)\})
\big) {}_{\overline{\mathcal A} }
=\nu_{a^1b^2}(\{(x_1,x_4)\}
\\
&
{}_{{\mathcal A}^*} \big(\rho_0,
F_{23}(\{(x_2,x_3)\})
\big) {}_{\overline{\mathcal A} }
=\nu_{a^2b^1}(\{(x_2,x_3)\},
\\
&
{}_{{\mathcal A}^*} \big(\rho_0,
F_{24}(\{(x_2,x_4)\})
\big) {}_{\overline{\mathcal A} }
=\nu_{a^2b^2}(\{(x_2,x_4)\}
\end{align}
Now we have the following problem:
| $(a):$ |
Does the observable
${\mathsf O}_{1234}{{=}} (\times_{k=1}^4
X_k ,
\times_{k=1}^4{\mathcal F}_k , F_{1234})$
in $\overline{\mathcal A}$
satisfying the following
($\sharp$)
exist?
| $(\sharp):$ |
$
\displaystyle
{\mathsf O}_{1234}^{(13)}
=
{\mathsf O}_{13},
\;\;
{\mathsf O}_{1234}^{(14)}
=
{\mathsf O}_{14},
\;\;
{\mathsf O}_{1234}^{(23)}
=
{\mathsf O}_{23},
\;\;
{\mathsf O}_{1234}^{(24)}
=
{\mathsf O}_{24}
\;\;
$
|
|
In what follows,
we show that
the above observable ${\mathsf O}_{1234}$
does not exist.
Answer.
Assume that
the observable
${\mathsf O}_{1234}{{=}} (\times_{k=1}^4
X_k , $
$
\times_{k=1}^4{\mathcal F}_k ,$
$ F_{1234})$
exists.
Then,
it suffices to show the contradiction.
Define
$C_{13}(\rho_0)$,
$C_{14}(\rho_0)$,
$C_{23}(\rho_0)$
and
$C_{24}(\rho_0)$
such that
\begin{align}
\left\{\begin{array}{ll}
\displaystyle
C_{13}(\rho_0)
=
\int_{\times_{k=1}^4 X_k} x_1 \cdot x_3
\;
{}_{{\mathcal A}^*} \big(\rho_0,
F_{1234}(
\times_{k=1}^4 dx_k
)
\big) {}_{\overline{\mathcal A} }
\\
\hspace{1.1cm}
\bigl(
=
\int_{X_1 \times X_3} x_1 \cdot x_3
\;
\nu_{a^1 b^1}
(
dx_1 dx_3)
\bigl)
\\
\displaystyle
C_{14}(\rho_0)
=
\int_{\times_{k=1}^4 X_k} x_1 \cdot x_4
\;
{}_{{\mathcal A}^*} \big(\rho_0,
F_{1234}(
\times_{k=1}^4 dx_k
)
\big) {}_{\overline{\mathcal A} }
\\
\hspace{1.1cm}
\bigl(=
\int_{X_1 \times X_4} x_1 \cdot x_4
\;
\nu_{a^1b^2}(
dx_1dx_4)
\bigl)
\\
\displaystyle
C_{23}(\rho_0)
=
\int_{\times_{k=1}^4 X_k} x_2 \cdot x_3
\;
{}_{{\mathcal A}^*} \big(\rho_0,
F_{1234}(
\times_{k=1}^4 dx_k
)
\big) {}_{\overline{\mathcal A} }
\\
\hspace{1.1cm}
\bigl(=
\int_{X_2 \times X_3} x_2 \cdot x_3
\;
\nu_{a^2b^1}(
dx_2dx_3)
\bigl)
\\
\displaystyle
C_{24}(\rho_0)
=
\int_{\times_{k=1}^4 X_k} x_2 \cdot x_4
\;
{}_{{\mathcal A}^*} \big(\rho_0,
F_{1234}(
\times_{k=1}^4 dx_k
)
\big) {}_{\overline{\mathcal A} }
\\
\hspace{1.1cm}
\bigl(=
\int_{X_2 \times X_4} x_2 \cdot x_4
\;
\nu_{a^2b^2}(
dx_2dx_4)
\bigl)
\end{array}\right.
\end{align}
Then,
we can easily get
the following Bell's inequality:
(cf. Bell's inequality (Thorem 4.17)).
\begin{align}
&
|C_{13}(\rho_0)-C_{14}(\rho_0)|
+
|C_{23}(\rho_0)+C_{24}(\rho_0)|
\nonumber
\\
{{\; \leqq \;}}
&
\int_{\times_{k=1}^4 X_k}
\!\!\!
| x_1 | \cdot |x_3-x_4|
\;\;+
\!\!
|x_2 | \cdot |x_3+x_4|
\big[F_{1234}(\times_{k=1}^4 dx_k )\big](\rho_0)
\nonumber
\\
{{\; \leqq \;}}
&
2
\qquad
(\mbox{since } x_k \in \{-1, 1\} )
\tag{8.11}
\end{align}
However,
the formula
(4.51)
says that
this (8.11) must be
$2{\sqrt 2}$.
Thus,
by contradiction,
we says that
${\mathsf O}_{1234}$ satisfying (a)
does not exist.
Thus we can not take a measurement
${\mathsf M}_{\overline{\mathcal A}} (
{\mathsf O}_{1234},
S_{[\rho_0]}
)$.
However,
it should be noted that
| $(b):$ |
instead of
${\mathsf M}_{\overline{\mathcal A}} (
{\mathsf O}_{1234},
S_{[\rho_0]}
)$.
we can take a
parallel measurement
${\mathsf M}_{\otimes_{k=1}^4 \overline{\mathcal A}} (
{\mathsf O}_{13} \otimes
{\mathsf O}_{14} \otimes
{\mathsf O}_{23} \otimes
{\mathsf O}_{24}
,$
$
S_{[\otimes_{k=1}^4 \rho_0]})$.
In this case,
we easily see that
(8.11)
=
$2{\sqrt 2}$
as the formula
(4.51}).
|
That is,
| $(c):$ |
in the case of a parallel measurement,
Bell's inequality is broken
in both
quantum and classical systems.
|
| $\fbox{Note 8.2}$ |
In the above argument,
Bell's inequality is used in the framework
of measurement theory.
This is of course true.
Although the above argument is not related to the problem of "hidden variable",
it is interesting as how to use Bel's inequality.
|
