8.6: Syllogism---Does Socrates die?
8.6.1: Syllogism and its variations: Classical systems
Next,
we shall discuss
practical syllogism
(i.e.,
measurement theoretical theorem
concerning
implication (Definition8.6)
).
Before the discussion,
we note that
On the other hand,
in classical system,
we can expect that
syllogism holds.
This will be proved in the following theorem.
Let
${\mathsf O}_{123}$
$=$
$(X_1 \times X_2 \times X_3,$
$ {\cal F}_1 \times {\cal F}_2 \times {\cal F}_3 ,$
$ F_{123}{}{{=}} {\mathop{\overset{qp}{\times}}}_{k=1,2,3} F_k)$
be an observable in
${L^\infty (\Omega)}$
Fix
$\omega \in \Omega $,
$\Xi_1$
$ \in {\cal F}_1$,
$\Xi_2$
$ \in {\cal F}_2$,
$\Xi_3$
$ \in {\cal F}_3$
Then,
we see
the following
(i)
$\mbox{--}$
(iii).
For the proof of (ii) and (iii),
see
my papers.
Let
${\mathsf O}_{{1}}$
${{=}}$
${\mathsf O}_{{{\scriptsize{\mbox{SW}}}}}$
${{=}}$
$(X_{{\scriptsize{\mbox{SW}}}} , $
$ 2^{ X_{{\scriptsize{\mbox{SW}}}} } ,$
$ F_{{\scriptsize{\mbox{SW}}}})$
and
${\mathsf O}_{{3}}$
${{=}}$
${\mathsf O}_{{\scriptsize{\mbox{RD}}}}$
${{=}}$
$(X_{{\scriptsize{\mbox{RD}}}} ,$
$ 2^{ X_{{\scriptsize{\mbox{RD}}}} } ,$
$ F_{{\scriptsize{\mbox{RD}}}})$
be as in Example 8.5.
Putting
$X_{{\scriptsize{\mbox{RP}}}}
=
\{ y_{{\scriptsize{\mbox{RP}}}} , n_{{\scriptsize{\mbox{RP}}}} \} $,
consider the new
observable
${\mathsf O}_{{2}}$
${{=}}$
${\mathsf O}_{{{\scriptsize{\mbox{RP}}}}}$
${{=}}$
$(X_{{\scriptsize{\mbox{RP}}}} , 2^{ X_{{\scriptsize{\mbox{RP}}}} } , F_{{\scriptsize{\mbox{RP}}}})$.
Here,
"$y_{{\scriptsize{\mbox{RP}}}}$"
and
"$n_{{\scriptsize{\mbox{RP}}}}$"
respectively means
"ripe"
and
"not ripe".
Put
Consider the following quasi-product observable:
Let
${{\omega_k}}$
$\in \Omega$.
And assume that
Then,
by
Theorem 8.12 (i),
we get:
Therefore,
when we know that
the tomato
${{\omega_k}} $ is sweet
by
measurement
${\mathsf M}_{L^\infty (\Omega)} ( {\mathsf O}_{123} , S_{[{}{{{\omega_k}} }]}) $,
the probability that
${{\omega_k}} $
is red
is given by
Of course, (8.14)
means
Therefore, by (8.12),
we get the following conclusion.
However,
it is not useful in the market.
What we want to know
is such as
When we observe that
the tomato
$\omega_n $
is "RED"$\!\!,\;$
we can infer,
by
the fuzzy inference
${\mathsf M}_{L^\infty(\Omega)}( {\mathsf O}_{13} ,$
$ S_{ [\delta_{\omega_n}{}] }) $,
the probability that
the tomato
$\omega_n $
is "SWEET"
is given by
Note that (8.16)
implies
(and is implied by)
And note that
the conclusion (8.17)
is somewhat like
Therefore,
the estimation (8.17)
may be useful in marckets.
$(\sharp):$ Since Theorem 8.9
( The existence of the combined observable)
does not hold in quantum system,
(
cf.
Counter Example 8.10 ),
syllogism does not hold.
Theorem 8.12 [Practical syllogism in classical systems]
Consider the classical basic structure
\begin{align}
[C_0(\Omega ) \subseteq L^\infty ( \Omega, \nu ) \subseteq B(L^2 ( \Omega, \nu ))]
\end{align}
(i).(practical syllogism)
\begin{align}
[{\mathsf O}_{123}^{(1)};{\Xi_1}]
\underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} ,
S_{ [\omega] }) }{ \Longrightarrow}
[{\mathsf O}_{123}^{(2)};{\Xi_2}] ,
\quad
[{\mathsf O}_{123}^{(2)};{\Xi_2}]
\underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} ,
S_{ [\omega] }) }{ \Longrightarrow}
[{\mathsf O}_{123}^{(3)};{\Xi_3}]
\end{align}
implies
\begin{align}
&
\; \;
\rm{Rep}_\omega^{\Xi_1 \times \Xi_3}[{}{\mathsf O}^{(13)}_{123}]
=
\left[\begin{array}
[{}F^{(13)}_{123} (\Xi_1 \times \Xi_3)] (\omega)
&
[{}F^{(13)}_{123} (\Xi_1 \times \Xi_3^c)]
(\omega)
\\
{}
[{}F^{(13)}_{123} (\Xi_1^c \times \Xi_3)]
(\omega)
&
[{}F^{(13)}_{123} (\Xi_1^c \times \Xi_3^c)]
(\omega)
\end{array}\right]
\\
=
&
\left[\begin{array}
[F^{(1)}_{123}(\Xi_1)](\omega)
&
0
\\
{}
[F^{(3)}_{123}(\Xi_3)](\omega)
-
[F^{(1)}_{123}(\Xi_1)](\omega)
&
1-
[F^{(3)}_{123}(\Xi_3)](\omega)
\end{array}\right]
\end{align}
That is, it holds:
\begin{align}
[{\mathsf O}_{123}^{(1)};{\Xi_1}]
\underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} ,
S_{ [\omega] }) }{ \Longrightarrow}
[{\mathsf O}_{123}^{(3)};{\Xi_3}]
\tag{8.12}
\end{align}
(ii).
\begin{align}
[{\mathsf O}_{123}^{(1)};{\Xi_1}]
\underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} ,
S_{ [\omega] }) }{ \Longleftarrow}
[{\mathsf O}_{123}^{(2)};{\Xi_2}] ,
\quad
[{\mathsf O}_{123}^{(2)};{\Xi_2}]
\underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} ,
S_{ [\omega] }) }{ \Longrightarrow}
[{\mathsf O}_{123}^{(3)};{\Xi_3}]
\end{align}
implies
\begin{align}
&
\; \;
\rm{Rep}_\omega^{\Xi_1 \times \Xi_3}[{}{\mathsf O}^{(13)}_{123}]
=
\left[\begin{array}
[{}F^{(13)}_{123} (\Xi_1 \times \Xi_3)] (\omega)
&
[{}F^{(13)}_{123} (\Xi_1 \times \Xi_3^c)]
(\omega)
\\
{}
[{}F^{(13)}_{123} (\Xi_1^c \times \Xi_3)]
(\omega)
&
[{}F^{(13)}_{123} (\Xi_1^c \times \Xi_3^c)]
(\omega)
\end{array}\right]
\\
=
&
\left[\begin{array}
\alpha_{_{\Xi_1 \times \Xi_3}}
&\;\;\;\;
[F^{(1)}_{123}(\Xi_1)](\omega)-\alpha_{_{\Xi_1 \times \Xi_3}}
\\
{}
[F^{(3)}_{123}(\Xi_3)](\omega)-\alpha_{_{\Xi_1 \times \Xi_3}}
&\;\;\;\;
1-\alpha_{_{\Xi_1 \times \Xi_3}}
-
[F^{(1)}_{123}(\Xi_1)]
-
[F^{(3)}_{123}(\Xi_3)]
\end{array}\right]
\end{align}
where
\begin{align}
&
\hspace{-1cm}
\max \{
[F^{(2)}_{123}(\Xi_2)](\omega),
[F^{(1)}_{123}(\Xi_1)](\omega)+
[F^{(3)}_{123}(\Xi_3)](\omega) - 1 \}
\nonumber
\\
&
\hspace{0.5cm}{{\; \leqq \;}}
\alpha_{_{\Xi_1 \times \Xi_3}} (\omega)
{{\; \leqq \;}}
\min \{ [F^{(1)}_{123}(\Xi_1)](\omega) , [F^{(3)}_{123}(\Xi_3)](\omega) \}
\tag{8.13}
\end{align}
(iii).
\begin{align}
[{\mathsf O}_{123}^{(1)};{\Xi_1}]
\underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} ,
S_{ [\omega] }) }{ \Longrightarrow}
[{\mathsf O}_{123}^{(2)};{\Xi_2}] ,
\quad
[{\mathsf O}_{123}^{(2)};{\Xi_2}]
\underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} ,
S_{ [\omega] }) }{ \Longleftarrow}
[{\mathsf O}_{123}^{(3)};{\Xi_3}]
\end{align}
implies
\begin{align}
&
\; \;
\rm{Rep}_\omega^{\Xi_1 \times \Xi_3}[{}{\mathsf O}^{(13)}_{123}]
=
\left[\begin{array}
[{}F^{(13)}_{123} (\Xi_1 \times \Xi_3)] (\omega)
&
[{}F^{(13)}_{123} (\Xi_1 \times \Xi_3^c)]
(\omega)
\\
{}
[{}F^{(13)}_{123} (\Xi_1^c \times \Xi_3)]
(\omega)
&
[{}F^{(13)}_{123} (\Xi_1^c \times \Xi_3^c)]
(\omega)
\end{array}\right]
\\
=
&
\left[\begin{array}
\alpha_{_{\Xi_1 \times \Xi_3}} (\omega)
&\;\;\;\;
[F^{(1)}_{123}(\Xi_1)](\omega)-\alpha_{_{\Xi_1 \times \Xi_3}} (\omega)
\\
{}
[F^{(3)}_{123}(\Xi_3)](\omega)-\alpha_{_{\Xi_1 \times \Xi_3}} (\omega)
&\;\;\;\;
1-\alpha_{_{\Xi_1 \times \Xi_3}} (\omega)
-
[F^{(1)}_{123}(\Xi_1)](\omega)
-
[F^{(3)}_{123}(\Xi_3)](\omega)
\end{array}\right]
\end{align}
where
\begin{align}
&
\hspace{-1cm}
\max \{ 0 , [F^{(1)}_{123}(\Xi_1)](\omega) + [F^{(3)}_{123}(\Xi_3)](\omega)
- [F^{(2)}_{123}(\Xi_2)](\omega) \}
\\
& \hspace{1cm}
{{\; \leqq \;}}
\alpha_{_{\Xi_1 \times \Xi_3}} (\omega)
{{\; \leqq \;}}
\min \{[F^{(1)}_{123}(\Xi_1)](\omega) ,
[F^{(3)}_{123}(\Xi_3)](\omega)
\}
\end{align}
Proof.
$\;\;$
(i):
By the condition,
we see
$\;\;$
\begin{align}
&
0=
[F^{(12)}_{123}(\Xi_1 \times \Xi_2^c )](\omega)
=
[F_{123}(\Xi_1 \times \Xi_2^c \times \Xi_3 )](\omega)
+
[F_{123}(\Xi_1 \times \Xi_2^c \times \Xi_3^c )](\omega)
\\
&
0=
[F^{(23)}_{123}(\Xi_2 \times \Xi_3^c )](\omega)
=
[F_{123}(\Xi_1 \times \Xi_2 \times \Xi^c_3 )](\omega)
+
[F_{123}(\Xi_1^c \times \Xi_2 \times \Xi_3^c )](\omega)
\end{align}
Therefore,
\begin{align}
&
0=
[F_{123}(\Xi_1 \times \Xi_2^c \times \Xi_3 )](\omega)
=
[F_{123}(\Xi_1 \times \Xi_2^c \times \Xi_3^c )](\omega)
\\
&
0=
[F_{123}(\Xi_1 \times \Xi_2 \times \Xi^c_3 )](\omega)
=
[F_{123}(\Xi_1^c \times \Xi_2 \times \Xi_3^c )](\omega)
\end{align}
Hence,
\begin{align}
&
[F^{(13)}_{123}(\Xi_1 \times \Xi_3^c )](\omega)
=
[F_{123}(\Xi_1 \times \Xi_2 \times \Xi_3^c )](\omega)
+
[F^{(13)}_{123}(\Xi_1 \times \Xi_2^c \times \Xi_3^c )](\omega)
=0
\end{align}
Thus, we get (8.12).
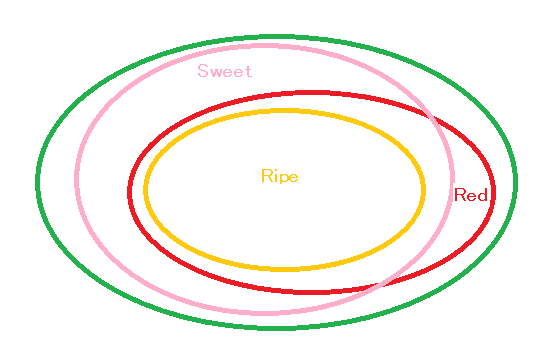
 Example 8.13 [Continued from Example 8.5]
Example 8.13 [Continued from Example 8.5]
\begin{align}
&
[{\mathsf O}_{123}^{(1)};{\{y_{{\scriptsize{\mbox{SW}}}} \}}]
\underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} ,
S_{ [{\omega_k}] }) }{ \Longrightarrow}
[{\mathsf O}_{123}^{(2)};{\{y_{{\scriptsize{\mbox{RP}}}} \}}] ,
\nonumber
\\
&
[{\mathsf O}_{123}^{(2)};{\{y_{{\scriptsize{\mbox{RP}}}} \}}]
\underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} ,
S_{ [{\omega_k}] }) }{ \Longrightarrow}
[{\mathsf O}_{123}^{(3)};{\{y_{{\scriptsize{\mbox{RD}}}} \}}]
\tag{8.14}
\end{align}
\begin{align}
&
\; \;\;\;
\rm{Rep} [{}{\mathsf O}_{13}{}]
=
\left[\begin{array}
[{}F_{13} ( \{ y_{{{\scriptsize{\mbox{SW}}}}} \}\times \{ y_{{{\scriptsize{\mbox{RD}}}}} \}){}] ({{\omega_k}} )
&
[{}F_{13} ( \{ y_{{{\scriptsize{\mbox{SW}}}}} \}\times \{ n_{{{\scriptsize{\mbox{RD}}}}} \}){}] ({{\omega_k}} )
\\
{}[{}F_{13} ( \{ n_{{{\scriptsize{\mbox{SW}}}}} \}\times \{ y_{{{\scriptsize{\mbox{RD}}}}} \}){}] ({{\omega_k}} )
&
[{}F_{13} ( \{ n_{{{\scriptsize{\mbox{SW}}}}} \}\times \{ n_{{{\scriptsize{\mbox{RD}}}}} \}){}] ({{\omega_k}} )
\\
\end{array}\right]
\\
&
=
\left[\begin{array}
[{}F_{{\scriptsize{\mbox{SW}}}} (\{ y_{{\scriptsize{\mbox{SW}}}} \}){}]({{\omega_k}} ) & 0 \\
{}[{}F_{{\scriptsize{\mbox{RD}}}} (\{ y_{{\scriptsize{\mbox{RD}}}} \}){}]({{\omega_k}} ) - [{}F_{{\scriptsize{\mbox{SW}}}} (\{ y_{{\scriptsize{\mbox{SW}}}} \}){}]
({{\omega_k}} )
& 1 - [{}F_{{\scriptsize{\mbox{RD}}}} (\{ y_{{\scriptsize{\mbox{RD}}}} \}){}]({{\omega_k}} ) \\
\end{array}\right]
\end{align}
\begin{align}
&
\frac {
[{}F_{13} ( \{ y_{{{\scriptsize{\mbox{SW}}}}} \}\times
\{ y_{{{\scriptsize{\mbox{RD}}}}} \}){}] ({{\omega_k}} )
}
{
[{}F_{13} ( \{ y_{{{\scriptsize{\mbox{SW}}}}} \}\times \{ y_{{{\scriptsize{\mbox{RD}}}}} \}){}] ({{\omega_k}} )
+
[{}F_{13} ( \{ y_{{{\scriptsize{\mbox{SW}}}}} \}\times \{ n_{{{\scriptsize{\mbox{RD}}}}} \}){}] ({{\omega_k}} )
}
=
\frac{
[{}F_{{\scriptsize{\mbox{RD}}}} (\{ y_{{\scriptsize{\mbox{RD}}}} \}){}] ({{\omega_k}})
}
{
[{}F_{{\scriptsize{\mbox{RD}}}} (\{ y_{{\scriptsize{\mbox{RD}}}} \}){}] ({{\omega_k}})
}
=
1
\\
&
\tag{8.15}
\end{align}
Example 8.14 [Continued from Example 8.5]
Instead of (8.14), assume that
\begin{align}
{\mathsf O}_1^{ \{y_1 \}}
\underset{ {\mathsf M}_{L^\infty(\Omega) }({\mathsf O}_{12} ,S_{ [\delta_{\omega_n}{}] }) }
{ \Longleftarrow}
{\mathsf O}_2^{ \{y_2 \}} ,
\qquad
{\mathsf O}_2^{ \{y_2 \}}
\underset{ {\mathsf M}_{L^\infty(\Omega) }({\mathsf O}_{23} ,S_{[{}\delta_{\omega_n}{}] }) }
{ \Longrightarrow}
{\mathsf O}_3^{ \{y_3 \}} .
\tag{8.16}
\end{align}
If some may think that the (8.17) is strange,
see the following figure:
Supplement
 |
| $\qquad \quad $Fig. 1.1: The history of world-descriptions |
Of course, the most inportant is Theore 8.12 (i)[usual syllogizm], i.e.,
| $(\sharp_1):$ | Since Socrates is a man and all men are mortal, it follows that Socrates is mortal. |
